In this project, I will try to solve 75 Leetcode questions as listed in this link.

104. Maximum Depth of Binary Tree

Description

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2
Solution

The solution is quite simple. We just need to traverse the tree and count the depth. The depth of a node is the maximum depth of its children plus one. The depth of a leaf node is 1.

In this solution, I use DFS to traverse the tree. The time complexity is O(n) and the space complexity is O(n) (in the worst case, the tree is a linked list).

What is DFS?

DFS stands for Depth First Search. It is a graph traversal algorithm. The idea is to traverse the graph by going as deep as possible, and backtrack when we cannot go further. The DFS algorithm can be implemented using recursion or stack.

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        def dfs(node, depth):
            if node is None:
                return depth
            else:
                return max(dfs(node.left, depth+1), dfs(node.right, depth+1))
        
        return dfs(root, 0)
Complexity Analysis
  • Time complexity: O(n) because we need to traverse all the nodes in the tree once.
  • Space complexity: O(n) because we need to store the depth of each node in the stack.
  • Hidden space complexity: O(h) where h is the height of the tree. This is the space complexity of the recursion stack.

100. Same Tree

Description

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

  • The number of nodes in both trees is in the range [0, 100].
  • -10^4 <= Node.val <= 10^4
Solution

The naive idea that comes to my mind is to traverse the two trees simultaneously and compare the value of each node. But how to traverse the two trees simultaneously. So I use the DFS algorithm to traverse the two trees separately and store the values of the nodes in two lists. Then I compare the two lists.

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        def extract(node, values):
            if node is None:
                values.append(None)
            else:
                values.append(node.val)
                extract(node.left, values)
                extract(node.right, values)
        
        values_p = []
        values_q = []
        extract(p, values_p)
        extract(q, values_q)
        
        return values_p == values_q
Complexity Analysis
  • Time complexity: O(n) because we need to traverse all the nodes in the tree once.
  • Space complexity: O(n) because we need to store the values of all the nodes in the tree. More precisely, O(4n) because we need to store the values of two trees in two lists.

226. Invert Binary Tree

Description

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:

Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

Input: root = []
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 100].
  • -100 <= Node.val <= 100
Solution

Each TreeNode in the binary tree is defined as follows:

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

It contains three attributes: val, left, and right. The val attribute stores the value of the node. The left and right attributes store the left and right children of the node, respectively. If the node does not have a left or right child, the corresponding attribute is None. A node without children is called a leaf node. A binary tree is a tree in which each node has at most two children.

The idea of the solution is to traverse the tree and swap the left and right children of each node but keep the value of the node unchanged.

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def swap(node):
            if node is None:
                return
            else:
                node.left, node.right = node.right, node.left
                swap(node.left)
                swap(node.right)
        
        swap(root)
        return root

Explanation:

  • if the node is None, return None which is the base case of the recursion.
  • if the node is not None, swap the left and right children of the node, then recursively swap the left and right children of the left and right children of the node.
  • It is interesting that we can swap the left and right children of the node without temporary variables. This is because Python allows us to assign multiple variables at the same time. For example, a, b = b, a will swap the values of a and b. This is called tuple unpacking, which is an in-place operation.
  • The important step is to recursive step when we call swap(node.left) and swap(node.right) to swap the children of the left and right children of the node.
  • Because the root node is unchanged, we can return the root node as the output of the function.

What is in-place operation?

An in-place operation is an operation that changes the input directly without making a copy. For example, the swap operation a, b = b, a is an in-place operation because it does not require extra memory to store the result. The operation a += b is also an in-place operation because it changes the value of a directly.

124. Binary Tree Maximum Path Sum

Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Example 3:

Input: root = [1,-2,3]
Output: 4
Explanation: The optimal path is 3 -> 1 with a path sum of 3 + 1 = 4.

Example 4:

Input: root = [-2,1,3]
Output: 3
Explanation: The optimal path is just the node 3 with a path sum of 3.

Constraints:

  • The number of nodes in the tree is in the range [1, 3 * 10^4].
  • -1000 <= Node.val <= 1000
Solution

This is a hard-level question that I couldn’t think of a solution at first. Therefore, I tried to explain my thought process as follows with an expectation that I can come up with a solution along the way. Fortunately, it works :smile: (with the big help of Github Copilot)

Firstly, we need to clarify the problem.

  • What is non-empty path? It means that the path must contain at least one node.
  • Is the path with only one node a valid path? Yes, it is.

So the path can be a sub-tree but every node has atmost one child except the root node which can have two children. The path can also be a single node. The path sum is the sum of all nodes in the sub-tree. However, with this perspective, it is still not clear how to find the optimal sub-tree. Grid search is not a good idea because the number of sub-trees is exponential with respect to the number of nodes in the tree.

Let’s think in the style of a dynamic programming problem. We can define the sub-problem as follows:

Given a path and an adjacent node (the node that is connected to the first or the last node in the path), should we add the adjacent node to the path or not?

There are two scenarios to be considered:

  • If the node has a positive value.
  • If the node has a negative value but its children have positive values and greater than the absolute value of the node.

The first scenario is quite straightforward that it is always better to add the adjacent node to the path. The second scenario is a bit tricky because what if adding it and its children to the path does not benefit the path sum but adding it, its children, and its grandchildren to the path does. In this case, adding the node to the path is a good deal because it will benefit the path sum in the future.

Based on the above analysis, we can think about more general scenarios as follows:

  • If the node has a positive value, add it to the path.
  • If the node has a negative value, but the sub-path starting from its children has a positive value and greater than the absolute value of the node, add it to the path.

However, this is still not clear enough to get a deployable solution. But the thought process makes me realize an important observation that “each node has its left child’s optimal path sum and right child’s optimal path sum”. The previous approach is left-to-right scanning manner, when we try to add an adjacent node of the left (or right) of the path to the path. What if we consider a “Middle-Out” approach as

Given a node, what is the optimal path sum of the sub-tree rooted at the node? In other words, should we connect the node to its left child, right child, or both?

With this approach, we can define the optimal path sum of the sub-tree rooted at the node as follows:

  • The value of the node.
  • The value of the node plus the optimal path sum of its left child.
  • The value of the node plus the optimal path sum of its right child.

Finally, we can write the code as follows:

class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        def dfs(node):
            if node is None:
                return 0
            else:
                left = dfs(node.left)
                right = dfs(node.right)
                self.max_sum = max(self.max_sum, node.val, node.val + left, node.val + right, node.val + left + right)
                return max(node.val, node.val + left, node.val + right)
        
        self.max_sum = -float('inf')
        dfs(root)
        return self.max_sum

Explanation:

  • The base case of the recursion is when the node is None, we return 0. It is worth noting that we return 0 instead of None as in previous problems.
  • If the node is not None we then recursively call the function on its left and right children to get the optimal path sum of the sub-trees rooted at the left and right children of the node.
  • Then the optimal path sum rooted at the node is the maximum of node.val and node.val + left and node.val + right. It is worth noting that we must not consider the value node.val + left + right even though it might be the maximum. It is because if we consider this value, we will recursively consider a sub-tree in the node’s children as a valid path, which is not correct.

102. Binary Tree Level Order Traversal

Description

Given the root of a binary tree, return the level order traversal of its nodes’ values. (i.e., from left to right, level by level).

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 2000].
  • -1000 <= Node.val <= 1000
Solution

What is level order traversal?

The level order traversal of a binary tree is a traversal that visits the nodes level by level.

The idea of the solution is to traverse the tree and store the nodes in a list of lists. The first list contains the nodes at level 0, the second list contains the nodes at level 1, and so on. Instead of using DFS, we use BFS to traverse the tree.

What is BFS?

BFS stands for Breadth First Search. It is a graph traversal algorithm. The idea is to traverse the graph by going level by level. The BFS algorithm can be implemented using a queue.

The following code snippet shows how to implement a queue using a list. The queue is a data structure that supports two operations: enqueue and dequeue. The enqueue operation adds an item to the queue. The dequeue operation removes an item from the queue. The first item that is added to the queue is the first item that is removed from the queue. This is called First In First Out (FIFO).

# Simple implementation of a queue using a list
class Queue:
    def __init__(self):
        self.items = []
    
    def enqueue(self, item):
        self.items.append(item)
    
    def dequeue(self):
        return self.items.pop(0)
    
    def is_empty(self):
        return len(self.items) == 0

Here is the solution to the problem.

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if root is None:
            return []
        else:
            queue = Queue()
            queue.enqueue(root)
            levels = []
            while not queue.is_empty():
                level = []
                for _ in range(len(queue.items)):
                    node = queue.dequeue()
                    level.append(node.val)
                    if node.left is not None:
                        queue.enqueue(node.left)
                    if node.right is not None:
                        queue.enqueue(node.right)
                levels.append(level)
            return levels

Explanation:

  • The base case is when the root is None, we return an empty list.
  • If the root is not None, we then create a queue and enqueue the root to the queue.
  • In each level, we iteratively dequeue all the nodes in the queue and append their values to the level list. Then we enqueue the left and right children of the nodes to the queue. The size of the queue is the number of nodes in the current level. The for loop iterates over the nodes in the current level. It is worth noting that we must not use for node in queue.items because the size of the queue changes when we enqueue the left and right children of the nodes. Instead, we use for _ in range(len(queue.items)) which iterates over the exact number of nodes in the current level.
  • The algorithm terminates when the queue is empty. Then we return the levels list.

297. Serialize and Deserialize Binary Tree

Description

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:

Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

  • The number of nodes in the tree is in the range [0, 10^4].
  • -1000 <= Node.val <= 1000
Solution

The idea of the solution is to traverse the tree and store the nodes in a list and then reconstruct the tree from the list in the deserializer. I will use both DFS and BFS in the solution.

Reflection: After solving this problem with BFS (level order traversal) I realized that BFS is a more intuitive approach to traverse the tree because it is level by level, which might be more matched with my intuition (personally), moreover, in the problem’s description, the input is also in the level order format which triggers me to think about BFS first. However the DFS is a more suitable approach to serialize the tree because it is easier to reconstruct the tree from the list of nodes in the DFS order. In the BFS order, we need to keep track of the parent nodes with a queue to reconstruct the tree.

Solution with BFS

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        levels = []
        queue = Queue()
        queue.enqueue(root)
        while not queue.is_empty():
            level = []
            for _ in range(len(queue.items)):
                node = queue.dequeue()
                if node is None:
                    level.append(None)
                else:
                    level.append(node.val)
                    queue.enqueue(node.left)
                    queue.enqueue(node.right)
            levels.append(level)
        return levels

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode
        """
        if len(data) == 0:
            return None
        else:
            root = TreeNode(data[0][0])
            queue = Queue()
            queue.enqueue(root.left)
            queue.enqueue(root.right)
            for level in data[1:]:
                for node in level:
                    if node is None:
                        parent_child = queue.dequeue()
                        parent_child = None
                        queue.enqueue(None)
                        queue.enqueue(None)
                    else:
                        current_node = TreeNode(node)
                        parent_child = queue.dequeue()
                        parent_child = current_node
                        queue.enqueue(current_node.left)
                        queue.enqueue(current_node.right)
            return root
        

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

Explanation:

In the serializer, it is the BFS algorithm that is similar to the previous problem. So this explanation is mostly for the deserializer. Let’s consider the following example:

Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]
Encoded: [[1], [2, 3], [None, None, 4, 5]]

Let’s go through the deserializer step by step.

  • The base case is when the data is an empty list, we return None.
  • If the data is not an empty list, we then create a root node with the value of the first element in the first level of the data list. The data always starts with the root node.
  • Because it is a binary tree, therefore, each node always have two children (None is also considered as a child) except the leaf nodes. Therefore, it is safe to assume that the length of the data list is: 2^0 + 2^1 + 2^2 + ... + 2^(n-1) = 2^n - 1 where n is the number of levels in the tree. The first level has 1 node, the second level has 2 nodes, the third level has 4 nodes, and so on. In the example, the length of the data list is 7 which is equal to 2^3 - 1 where n = 3.
  • Revised: The above observation is incorrect :smile:. For example, the input [1,2,null,3,null,4,null,5] is the left-skewed tree with 5 nodes, with level 0 has 1 node (root), level 1 has 2 node (2 and null), level 3 has 2 node (3 and null, which are children of node 2) and so on.
  • After creating the root node, we then create a queue to manage which node we are adding the children to. We start by enqueueing the root’s left and right children to the queue. So after this step, we have a tree - to be built - with only the root node and a queue - to manage the parent nodes - with two children of the root node.
  • Then we iterate over the data list from the second level to the last level. In each level, we iterate over the nodes in the level. We have the following actions:
    • We create a TreeNode with the value of the current node in the data list. If the value is None, we still create a TreeNode with the value of None.
    • We dequeue the parent’s children from the queue. It can be the left or right child of the parent node
    • We assign the current node to the the dequeued child. If the value of the current node is None, we assign None to the child.
    • We enqueue the left and right children of the current node to the queue. If the value of the current node is None, we enqueue two None values instead.

Turn out that the above solution doesn’t work :joy::joy::joy: The reason is that, I misunderstood the problem. The problem requires us to serialize the tree to a string, not a list of lists. So I need to change the solution with the following changes:

  • The serializer returns a string instead of a list of lists.
  • The deserializer takes a string as input instead of a list of lists.
  • There is an index to manage the index of the current node in the data list.
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
import math

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        data = []
        if root is None:
            return ''

        queue = Queue()
        queue.enqueue(root)
        while not queue.is_empty():
            for _ in range(len(queue.items)):
                node = queue.dequeue()
                if node is None:
                    data.append('N')
                else:
                    data.append(str(node.val))
                    queue.enqueue(node.left)
                    queue.enqueue(node.right)
        return ','.join(data)

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode

        example: ['1', '2', '3', 'N', 'N', '4', '5', 'N', 'N', 'N', 'N']
        example 2: 
            input = '[1,2,null,3,null,4,null,5]'
            encoded = ['1', '2', 'N', '3', 'N', '4', 'N', '5', 'N', 'N', 'N']
        """

        data_list = data.split(',')

        if data_list == ['']:
            return None
        else:
            root = TreeNode(int(data_list[0]))
            queue = Queue()
            queue.enqueue(root)

            num_levels = int(math.log(len(data_list)+1, 2))

            index = 1 # to manage index of children in data_list

            while index < len(data_list):
                parent = queue.dequeue()
                left_child = TreeNode(int(data_list[index])) if data_list[index] != 'N' else None
                right_child = TreeNode(int(data_list[index+1])) if data_list[index+1] != 'N' else None
                index = index + 2 
                parent.left = left_child
                parent.right = right_child
                if left_child is not None:
                    queue.enqueue(left_child)
                if right_child is not None:
                    queue.enqueue(right_child)
            return root

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

Solution with DFS

# Definition for a binary tree node. We need to modify tree node to help this solution work
class MyTreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = 'N'
        self.right = 'N'

import math

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        data = []
        if root is None:
            return ''

        def dfs(node):
            if node is None:
                data.append('N')
            else:
                data.append(str(node.val))
                dfs(node.left)
                dfs(node.right)
        dfs(root)
        return ','.join(data)

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode

        example: 
            input = [1,2,3,null,null,4,5] in level order format
            encoded = [1,2,N,N,3,4,N,N,5,N,N] in preorder format
        example 2: 
            input = [1,2,null,3,null,4,null,5] in level order format
            encoded = [1,2,3,4,5,N,N,N,N,N] in preorder format
        """

        data_list = data.split(',')

        if data_list == ['']:
            return None
        else:
            root = MyTreeNode(int(data_list[0]))
            stack = [root]

            index = 1 # to manage index of children in data_list

            while index < len(data_list):
                node_val = data_list[index]
                if node_val == 'N':
                    parent = stack.pop()
                    if parent.left == 'N':
                        parent.left = None
                        stack.append(parent)
                    else:
                        parent.right = None
                else:
                    node = MyTreeNode(int(node_val))
                    parent = stack[-1]
                    if parent.left == 'N':
                        parent.left = node
                    else:
                        parent.right = node
                    stack.append(node)
                index = index + 1
            return root

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

Turn out that leetcode doesn’t allow me to implement MyTreeNode class, I don’t know why yet. So I gave up and found the superb solution from here

class Codec:
    def serialize(self, root):
        if not root: return 'x'
        return ','.join([str(root.val), self.serialize(root.left), self.serialize(root.right)])

    def deserialize(self, data):
		# The reason I use self.data in the deserialize is, data stream will be consumed  as we build left side of Tree
		# by the time when the right side is building up, we need to hold what is left over.
		# Therefore, self.data is a global value, right side will use what is left over after tree is partially built
        self.data = data
        if self.data[0] == 'x': return None
        node = TreeNode(self.data[:self.data.find(',')]) 
        node.left = self.deserialize(self.data[self.data.find(',')+1:])
        node.right = self.deserialize(self.data[self.data.find(',')+1:])
        return node

Extension: How to serialize a binary tree to a string with minimal length?

  • The first idea is to use level order traversal to serialize the tree. Whenever we encounter a sequence of None values, we replace it with 2 values None and numbers_of_None where numbers_of_None is the number of None values in the sequence. For example, the sequence [1, 2, None, None, None, 3, 4, None, None, None, None] will be serialized to [1, 2, None, 3, 4, None, 4]. This approach will be beneficial when the tree is sparse.
  • The second idea is to pre-define a set of encode-decode rules that know in both sides. We then self-analyze the tree and encode it with optimal rules. The optimal rule also be sent to the other side to decode the tree. For example, the outer tree [1, 2, 3, 4, None, None, 5] can be encode as out [1, 2, 3, 4, 5].

572. Subtree of Another Tree

Description

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node’s descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

Example 2:

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

Constraints:

  • The number of nodes in the root tree is in the range [1, 2000].
  • The number of nodes in the subRoot tree is in the range [1, 1000].
  • -10^4 <= root.val <= 10^4
  • -10^4 <= subRoot.val <= 10^4
Solution

The idea is to traverse the tree and convert to a list. If the list of the sub-tree is a sub-list of the list of the tree, then the sub-tree is a sub-tree of the tree. But we must use DFS instead of BFS because the order of the nodes in the list matters and DFS preserves the order of the nodes.

class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        def dfs(node):
            if node is None:
                return 'N'
            else:
                return str(node.val) + ',' + dfs(node.left) + ',' + dfs(node.right)
        tree = dfs(root)
        sub_tree = dfs(subRoot)
        return sub_tree in tree

Turn out that the above approach just pass 181 over 182 test cases :joy:. The fail test case is actually very simple that I didn’t think of it. The test case is root=[12] and subroot=[2] so the function return True because the string 2 is in the string 12. The solution is adding special symbols at the begin and end of each node value

class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        def dfs(node):
            if node is None:
                return 'N'
            else:
                return '*' + str(node.val) + '*' + ',' + dfs(node.left) + ',' + dfs(node.right)
        tree = dfs(root)
        sub_tree = dfs(subRoot)
        return sub_tree in tree

My solution beats 98.03% of users with Python3 in term of Runtime :smile: but just 18.95% in term of Memory

105. Construct Binary Tree from Preorder and Inorder Traversal

Description

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

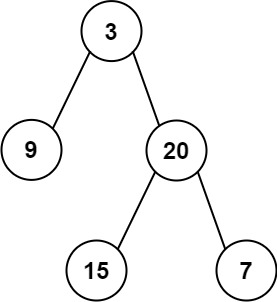
Example 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Constraints:

  • 1 <= preorder.length <= 3000
  • inorder.length == preorder.length
  • -3000 <= preorder[i], inorder[i] <= 3000
  • preorder and inorder consist of unique values.
  • Each value of inorder also appears in preorder.
  • preorder is guaranteed to be the preorder traversal of the tree.
  • inorder is guaranteed to be the inorder traversal of the tree.
Solution

The problem is a bit ambiguous to me in the first place, because normally if we have either preorder or inorder traversal, we can construct the tree. But in this problem, we need both lists. And the reason is because we don’t have None or null values in the lists to indicate the end of the left or right sub-tree. Therefore, we need both lists and match the values in the lists to construct the tree.

Some important observations:

  • The first element in the preorder list is always the root of the tree.
  • The root of the tree divides the inorder list into two parts: the left sub-tree and the right sub-tree.
  • The root of the left sub-tree is the one in the preorder list that is right after the root of the tree.

Based on the above observations, here is the solution

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if len(preorder) == 0:
            return None
        else:
            root = TreeNode(preorder[0])
            root_index = inorder.index(preorder[0])
            root.left = self.buildTree(preorder[1:root_index+1], inorder[:root_index])
            root.right = self.buildTree(preorder[root_index+1:], inorder[root_index+1:])
            return root

98. Validate Binary Search Tree

Description

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node’s key.
  • The right subtree of a node contains only nodes with keys greater than the node’s key.
  • Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3]
Output: true

Example 2:

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Constraints:

  • The number of nodes in the tree is in the range [1, 10^4].
  • -2^31 <= Node.val <= 2^31 - 1
Solution

Clarification:

  • What if the tree like this [5, 1, 6, null, null, 3, 7]? It violates the BST property because the left child of 6 is 3 which is smaller than its grandparent 5. Therefore the expected output is False.

So the solution is to use inorder traversal to traverse the tree and check if the values are in ascending order.


class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        output = []
        def inorder_traversal(root):
            if root is not None:
                inorder_traversal(root.left)
                output.append(root.val)
                inorder_traversal(root.right)
        inorder_traversal(root)
        return output == sorted(output) and len(output) == len(set(output))

230. Kth Smallest Element in a BST

Description

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

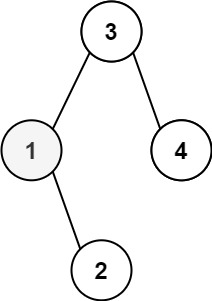
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

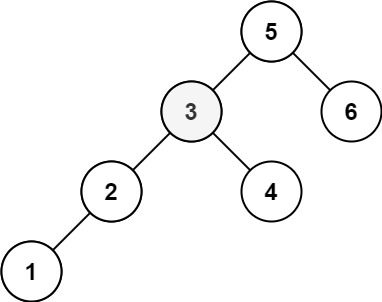
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

  • The number of nodes in the tree is n.
  • 1 <= k <= n <= 10^4
  • 0 <= Node.val <= 10^4
Solution

Similar to the above problem 98. Validate Binary Search Tree, we can use inorder traversal to traverse the tree and store the values in a list. Then we return the kth element in the list.

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        output = []
        def inorder_traversal(root):
            if root is not None:
                inorder_traversal(root.left)
                output.append(root.val)
                inorder_traversal(root.right)
        inorder_traversal(root)
        return output[k-1]

My solution beats 90.98% of users with Python3 in term of Runtime and 95.87% in term of Memory

235. Lowest Common Ancestor of a Binary Search Tree

Description

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor of two nodes p and q in a binary search tree (BST) is the lowest node in the tree that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

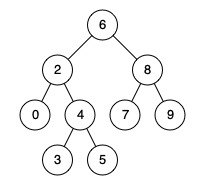
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [2, 10^5].
  • -10^9 <= Node.val <= 10^9
  • All Node.val are unique.
  • p != q
  • p and q will exist in the BST.
Solution

Important observations:

  • The tree is BST, therefore, by definition, the left sub-tree of a node contains only nodes with keys less than the node’s key and the right sub-tree of a node contains only nodes with keys greater than the node’s key.
  • we can check if the values of the root is between the values of the two nodes. If yes, then the root is the LCA. Otherwise, we can recursively check the left or right sub-tree of the root.
class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if root.val > p.val and root.val > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        elif root.val < p.val and root.val < q.val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return root

Another solution that might run faster and avoid recursion is to use a while loop which I found from here.

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while root:
            if root.val > p.val and root.val > q.val:
                root = root.left
            elif root.val < p.val and root.val < q.val:
                root = root.right
            else:
                return root

208. Implement Trie (Prefix Tree)

Description

A trie (pronounced as “try”) or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.

Implement the Trie class:

  • Trie() Initializes the trie object.
  • void insert(String word) Inserts the string word into the trie.
  • boolean search(String word) Returns true if the string word is in the trie (i.e., was inserted before), and false otherwise.
  • boolean startsWith(String prefix) Returns true if there is a previously inserted string word that has the prefix prefix, and false otherwise.

Example 1:

Input
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
Output
[null, null, true, false, true, null, true]

Explanation
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // return True
trie.search("app");     // return False
trie.startsWith("app"); // return True
trie.insert("app");
trie.search("app");     // return True

Constraints:

  • 1 <= word.length, prefix.length <= 2000
  • word and prefix consist only of lowercase English letters.
  • At most 3 * 10^4 calls in total will be made to insert, search, and startsWith.
Solution

We will use dictionary for this problem (I don’t understand why this question classified as a Tree problem). We can use one dictionary to store words and another dictionary to store all posible prefixes.

class Trie:

    def __init__(self):
        self.word_dict = dict()
        self.prefix_dict = dict()
    
    def break_word(self, word):
        return [word[:i] for i in range(1, len(word)+1)]

    def insert(self, word: str) -> None:
        self.word_dict[word] = True
        for prefix in self.break_word(word):
            self.prefix_dict[prefix] = True

    def search(self, word: str) -> bool:
        return word in self.word_dict
        

    def startsWith(self, prefix: str) -> bool:
        return prefix in self.prefix_dict


# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)

Surprisingly, my solution beats 94.76% of users with Python 3 in term of Memory even though I use two dictionaries.

211. Design Add and Search Words Data Structure

Description

Design a data structure that supports adding new words and finding if a string matches any previously added string.

Implement the WordDictionary class:

  • WordDictionary() Initializes the object.
  • void addWord(word) Adds word to the data structure, it can be matched later.
  • bool search(word) Returns true if there is any string in the data structure that matches word or false otherwise. word may contain dots ‘.’ where dots can be matched with any letter.

Example 1:

Input
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
Output
[null,null,null,null,false,true,true,true]

Explanation
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True

Constraints:

  • 1 <= word.length <= 500
  • word in addWord consists lower-case English letters.
  • word in search consist of ‘.’ or lower-case English letters.
  • There will be at most 2 dots in word for search queries.
  • At most 10000 calls will be made to addWord and search.
Solution

We can still use dictionary as in the previous problem, but with a bit modification. We need a specific function to replace at most two characters in each word by dot and store the new words in the dictionary.

class WordDictionary:

    def __init__(self):
        self.word_dict = dict()

    def replace_char(self, word):
        output = []
        # replace one character
        for i in range(len(word)):
            output.append(word[:i] + '.' + word[i+1:])
        # replace two characters
        for i in range(len(word)):
            for j in range(i+1, len(word)):
                output.append(word[:i] + '.' + word[i+1:j] + '.' + word[j+1:])
        return output
    

    def addWord(self, word: str) -> None:
        self.word_dict[word] = True
        for new_word in self.replace_char(word):
            self.word_dict[new_word] = True

    def search(self, word: str) -> bool:
        return word in self.word_dict


# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)

Turn out that my solution is bad :joy: because it beats only 5% of users with Python 3 in term of Runtime and Memory. Maybe we need a Tree approach. I think my solution might be good in the scenario when we need search more than addWord operations. Because the heaviest task is to break the word into new words and store them in the dictionary.

212. Word Search II

Description

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

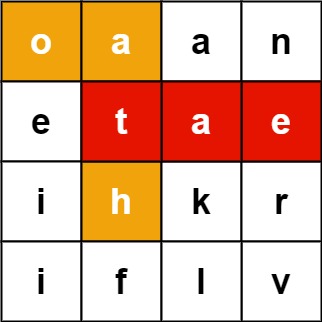
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

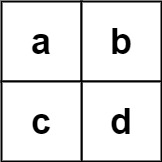
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 12
  • board[i][j] is a lowercase English letter.
  • 1 <= words.length <= 3 * 104
  • 1 <= words[i].length <= 10
  • words[i] consists of lowercase English letters.
  • All the strings of words are unique.
Solution

I have to refer to some solutions (here and here) to find out how to solve this problem. The idea is to use Trie to store the words and use DFS to traverse the board to find all possible words.

Clarification: Because the same letter cell may not be used more than once in a word, we need to keep track of the visited cells in the board. We can use a set to store the visited cells or we can modify the board by replacing the visited cells with a special character (e.g. #), but it will cost more memory because we need to carry out the modified board recursively.

class TrieNode:
    def __init__(self):
        self.children = dict()
        self.isEndOfWord = False

class Trie:
    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, word):
        node = self.root
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.isEndOfWord = True
    
    def search(self, word):
        node = self.root
        for char in word:
            if char not in node.children:
                return False
            node = node.children[char]
        return node.isEndOfWord or node is not None

def add_boundary(board):
    """
    a helper function to add boundary to the board
    board with size m x n --> board with size (m+2) x (n+2)
    """
    m = len(board)
    n = len(board[0])
    new_board = [['#'] * (n+2)]
    for i in range(m):
        new_board.append(['#'] + board[i] + ['#'])
    new_board.append(['#'] * (n+2))
    return new_board
    

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        def build_trie(self, board):
            self.trie = Trie()

        
        self.build_trie(board)
        output = []
        for word in words:
            if self.trie.search(word):
                output.append(word)
        return output

Reflection: Binary Tree Problems?

This is a placeholder for me to reflect what I have learned to solve the binary tree problems. So far

  • Tree traversal algorithms are the foundation of solving binary tree problems.
  • Recursion and Recursive thinking
  • The base case of the recursion is very important. It is the condition that stops the recursion.
  • Trie is a tree data structure that is used to store strings. It is very useful in solving string problems.

I also found that the following resources are very useful:

Revisit: Tree Traversal Techniques

Source: https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/

What is tree traversal?

Tree traversal is the process of visiting (checking and/or updating) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. Two most important ways are traversal by level (BFS) and traversal by depth (DFS).

Tree Traversal Example
Inorder Traversal

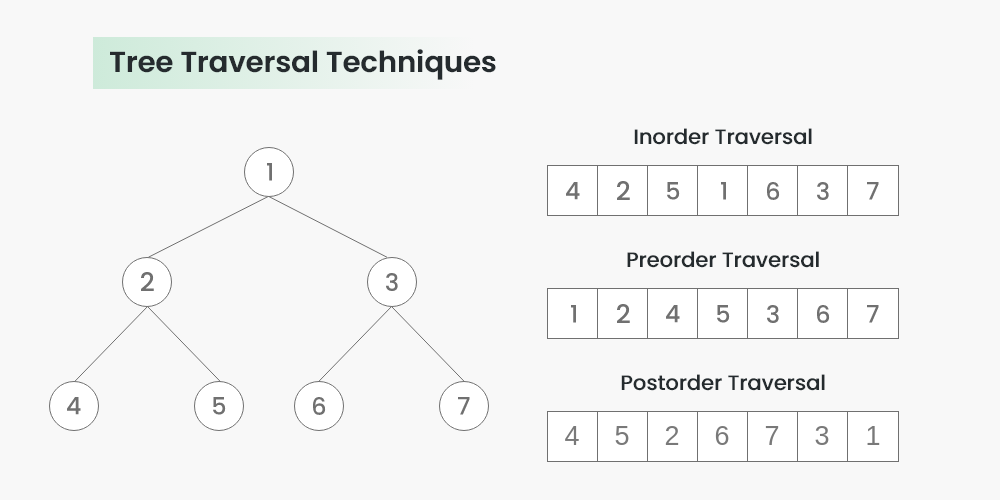
Inorder Traversal Algorithm

  1. Traverse the left subtree, i.e., call Inorder(left-subtree)
  2. Visit the root.
  3. Traverse the right subtree, i.e., call Inorder(right-subtree)
# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def inorder_traversal(root):
    if root is None:
        return
    else:
        inorder_traversal(root.left)
        print(root.val)
        inorder_traversal(root.right)
Preorder Traversal

Preorder Traversal Algorithm

  1. Visit the root.
  2. Traverse the left subtree, i.e., call Preorder(left-subtree)
  3. Traverse the right subtree, i.e., call Preorder(right-subtree)
# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def preorder_traversal(root):
    if root is None:
        return
    else:
        print(root.val)
        preorder_traversal(root.left)
        preorder_traversal(root.right)

Problems:

Postorder Traversal

Postorder Traversal Algorithm

  1. Traverse the left subtree, i.e., call Postorder(left-subtree)
  2. Traverse the right subtree, i.e., call Postorder(right-subtree)
  3. Visit the root.
# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def postorder_traversal(root):
    if root is None:
        return
    else:
        postorder_traversal(root.left)
        postorder_traversal(root.right)
        print(root.val)
Level Order Traversal

Level Order Traversal Algorithm

  1. Create an empty queue q
  2. Enqueue root to q
  3. Loop while q is not empty
    a. Dequeue a node from q and print its value
    b. Enqueue node’s children (first left then right children) to q if they are not null
# Simple implementation of a queue using a list
class Queue:
    def __init__(self):
        self.items = []
    
    def enqueue(self, item):
        self.items.append(item)
    
    def dequeue(self):
        return self.items.pop(0)
    
    def is_empty(self):
        return len(self.items) == 0

The following code snippet shows how to implement the BFS algorithm to traverse the tree.

# Simple BFS implementation
def bfs(root):
    queue = Queue()
    queue.enqueue(root)
    while not queue.is_empty():
        node = queue.dequeue()
        print(node.val)
        if node.left is not None:
            queue.enqueue(node.left)
        if node.right is not None:
            queue.enqueue(node.right)

Revisit Trie Data Structure

Source: https://www.geeksforgeeks.org/trie-insert-and-search/

What is Trie?

In short, Trie is a k-ary tree where k is the largest number of children of a node.

Because of its structure, Trie is an efficient information retrieval data structure. Using Trie, search complexities can be brought to optimal limit (key length). If we store keys in binary search tree, a well balanced BST will need time proportional to M * log N, where M is maximum string length and N is number of keys in tree. Using Trie, we can search the key in O(M) time. However the penalty is on Trie storage requirements.

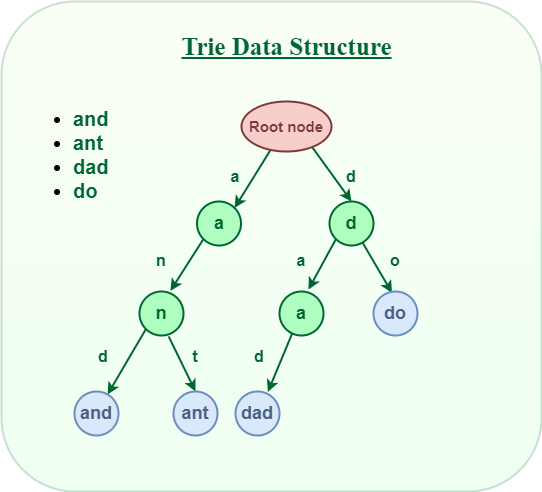
Trie Example. In this example, it is assumed that only English alphabets are used. Therefore, each node can have at most 26 children, even it looks like a binary tree.

The following code is a simple Trie for English alphabet.

class TrieNode:
     
    # Trie node class
    def __init__(self):
        self.children = [None]*26
 
        # isEndOfWord is True if node represent the end of the word
        self.isEndOfWord = False
Insert and Search Opeartions

To insert a key to Trie, we need to do the following steps:

  • Starting from the root, we check if the current node has a child corresponding to the first character of the key. If yes, we move to that child and continue to check the next character.
  • If no, we create a new node and link it to the current node.
  • We repeat the above steps until we reach the last character of the key. Then we mark the last node as the end of the key.
Insertion example

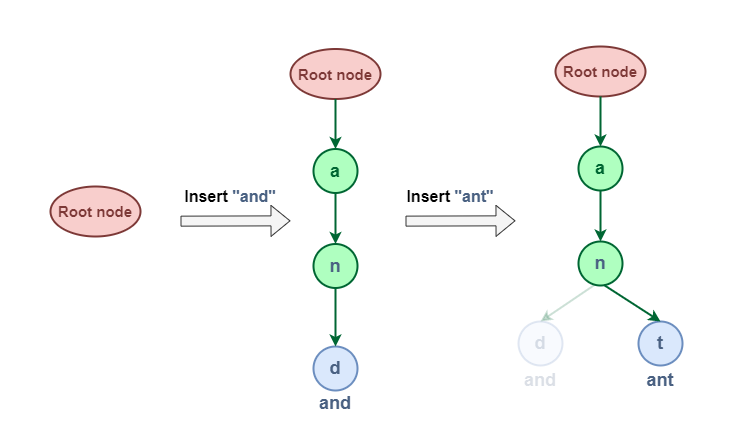
To search a key in Trie, we need to do the following steps:

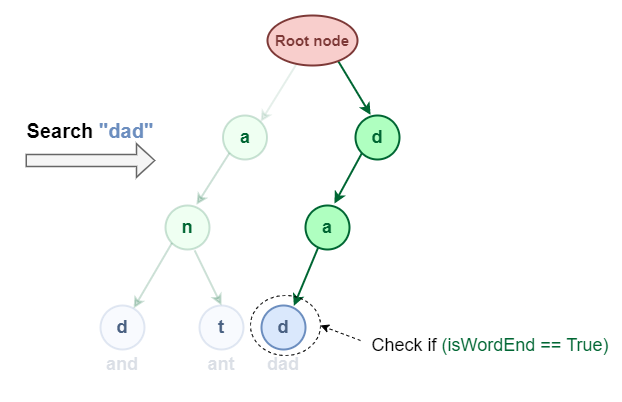
  • Starting from the root, we check if the current node has a child corresponding to the first character of the key. If yes, we move to that child and continue to check the next character.
  • If no, we return False.
  • We repeat the above steps until we reach the last character of the key. Then we return True if the last node is marked as the end of the key.
Search example 

def chartoIndex(ch):
    # private helper function
    # Converts key current character into index
    # use only 'a' through 'z' and lower case
    return ord(ch)-ord('a')

class Trie:

    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, key):
        cur = self.root 
        length = len(key)
        for level in range(length):
            index = chartoIndex(key[level])
            if not cur.children[index]:
                cur.children[index] = TrieNode()
            cur = cur.children[index]
        cur.isEndOfWord = True
    
    def search(self, key):
        cur = self.root
        length = len(key)
        for level in range(length):
            index = chartoIndex(key[level])
            if not cur.children[index]:
                return False
            cur = cur.children[index]
        return cur != None or cur.isEndOfWord

Another implementation of Trie is to use dictionary which is preferred in Leetcode.

class TrieNode:
    def __init__(self):
        self.children = dict()
        self.isEndOfWord = False

class Trie:
    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, word):
        cur = self.root
        for ch in word:
            if ch not in cur.children:
                cur.children[ch] = TrieNode()
            cur = cur.children[ch]
        cur.isEndOfWord = True
    
    def search(self, word):
        cur = self.root
        for ch in word:
            if ch not in cur.children:
                return False
            cur = cur.children[ch]
        return cur != None or cur.isEndOfWord