Hackerrank Questions
In this project, I will try to solve Hackerrank problems using Python. I started with the “One week Preparation Kit” with total 21 problems and 7 mock tests.
Tower Breakers
DescriptionTwo players are playing a game of Tower Breakers! Player \(1\) always moves first, and both players always play optimally. The rules of the game are as follows:
- Initially there are \(n\) towers.
- Each tower is of height \(m\).
- The players move in alternating turns.
- In each turn, a player can choose a tower of height \(x\) and reduce its height to \(y\), where \(y\) and \(x\) evenly divides (i.e. \(x \% y = 0\)) and \(1 \leq y < x\).
- If the current player is unable to make a move, they lose the game.
Given the values of \(n\) and \(m\), determine which player will win. If the first player wins, return \(1\). Otherwise, return \(2\).
SolutionSome observations:
- Regardless the height of a tower, the player can always reduce it to \(1\) and make it out of the games.
- If there are only 2 towers with even height, the second player can always adjust the height of the towers to be the same so that the total winning moves after his move is even number. So the first player will lose.
- Similarly if there are only 2 towers with odd height, the second player can also adjust the height and win.
- In general, if there are even number of towers with the same height (i.e., number of winning moves), the second player will win.
Given the above obseravtions, let’s work out strategy for the first player.
- If $n$ is odd, P1 plays the first move to reduce the height of the first tower to 1. The number of towers left is even, so P1 will win.
- If $n$ is even, P1 always lose because P2 can always adjust the height of the towers to be the same and the number of towers left is even.
Consider example:
- $n=2$ and $m=4$. If the first layer reduce the height of towers to [2, 4]. The total winning moves can be [1, 2] or [1, 1]. So the player 2 will choose the first option [1, 2] and win the game. Here is the game: P1 [2, 4] -> P2 [2, 2] -> P1 [1, 2] -> P2 [1, 1], player 2 win. The other scenarios will lead to the same result. P1 [1, 4] -> P2 [1, 1], player 2 win.
- $n=3$ and $m=3$. The total winning moves is 3, so the first player will win. [3, 3, 3] -> P1 [1, 3, 3] -> P2 [1, 1, 3] -> P1 [1, 1, 1]. or [3, 3, 3] -> P1 [1, 3, 3] -> P2 [1, 2, 3] -> P1 [1, 2, 2] -> P2 [1, 1, 2] -> P1 [1, 1, 1], player 1 win.
- $n=3$ and $m=4$. The total winning moves is 6, so the play 2 win.
- [4, 4, 4] -> P1 [1, 4, 4] -> P2 [1, 2, 4] -> P1 [1, 2, 2]
Exception:
- when $n=1$, the first player will win regardless the height of the tower because he can always reduce it to 1, except when $m=1$.
- when $m=1$, the first player will lose regardless the number of towers because he can not make any move.
def towerBreakers(n, m):
if n == 1 and m > 1:
return 1
if m == 1:
return 2
if n % 2 == 1:
return 2
else:
return 1
Caesar Cipher
DescriptionJulius Caesar protected his confidential information by encrypting it using a cipher. Caesar’s cipher shifts each letter by a number of letters. If the shift takes you past the end of the alphabet, just rotate back to the front of the alphabet. In the case of a rotation by 3, w, x, y and z would map to z, a, b and c.
Original alphabet: abcdefghijklmnopqrstuvwxyz
Alphabet rotated +3: defghijklmnopqrstuvwxyzabc
For example, the given cleartext \(s = There's-a-starman-waiting-in-the-sky\) and the alphabet is rotated by \(k = 3\). The encrypted string is \(Wkhuh'v-d-vwdupdq-zdlwlqj-lq-wkh-vnb\).
Note: The cipher only encrypts letters; symbols, such as -, remain unencrypted.
Solutiondef caesarCipher(s, k):
# Write your code here
alphabet = 'abcdefghijklmnopqrstuvwxyz'
length_alphabet = len(alphabet)
shift = k % length_alphabet
shifted_alphabet = alphabet + alphabet
shifted_alphabet = shifted_alphabet[shift:shift+length_alphabet]
map_dict = {}
for old, new in zip(alphabet, shifted_alphabet):
map_dict[old] = new
map_dict[old.upper()] = new.upper()
output = ''
for c in s:
if c in map_dict:
output += map_dict[c]
else:
output += c
return output
Palindrome Index
DescriptionGiven a string of lowercase letters in the range \(ascii[a-z]\), determine a character that can be removed to make the string a palindrome. There may be more than one solution, but any will do. For example, if \(s = bcbc\), we can either remove \(b\) at index \(0\) or \(c\) at index \(3\). If the word is already a palindrome or there is no solution, return \(-1\). Otherwise, return the index of a character to remove.
Solutiondef palindromeIndex(s):
# Write your code here
if s == s[::-1]:
return -1
for i in range(len(s)):
if s[i] != s[-i-1]:
if s[i+1] == s[-i-1] and s[i+2] == s[-i-2]:
return i
else:
return len(s) - i - 1
Grid Challenge
DescriptionGiven a square grid of characters in the range ascii[a-z], rearrange elements of each row alphabetically, ascending. Determine if the columns are also in ascending alphabetical order, top to bottom. Return YES if they are or NO if they are not.
For example, given the grid grid=['abc', 'ade', 'efg']
a b c
a d e
e f g
The rows are already in alphabetical order. The columns \(a\), \(a\), and \(e\) are also in alphabetical order, so the answer would be YES. Only elements within the same row can be rearranged. They cannot be moved to a different row.
SolutionMap each character to an integer, sort each row, then calculate the different (gradient) between two adjacent characters in each row. If the gradient is negative, then the row is not in ascending order. If all rows are in ascending order, then check the columns.
def gridChallenge(grid):
# Write your code here
n = len(grid)
m = len(grid[0])
grid_int = []
for row in grid:
grid_int.append([ord(c) for c in row])
# sorting
for row in grid_int:
row.sort()
for row in grid_int:
for i in range(m-1):
if row[i] > row[i+1]:
return 'NO'
for j in range(m):
for i in range(n-1):
if grid_int[i][j] > grid_int[i+1][j]:
return 'NO'
return 'YES'
Another solution is convert to 2D numpy array (but Hackerrank does not support numpy!)
def gridChallenge(grid):
# Write your code here
n = len(grid)
m = len(grid[0])
grid_int = []
for row in grid:
grid_int.append([ord(c) for c in row])
grid_int = np.array(grid_int)
grid_int = np.reshape(grid_int, (n, m))
# sorting
grid_int.sort(axis=1)
row_diff = grid_int[:, 1:] - grid_int[:, :-1]
if np.any(row_diff < 0):
return 'NO'
col_diff = grid_int[1:, :] - grid_int[:-1, :]
if np.any(col_diff < 0):
return 'NO'
return 'YES'
Recursive Digit Sum
DescriptionWe define super digit of an integer \(x\) using the following rules:
- If \(x\) has only \(1\) digit, then its super digit is \(x\).
- Otherwise, the super digit of \(x\) is equal to the super digit of the digit-sum of \(x\). Here, digit-sum of a number is defined as the sum of its digits.
For example, super digit of \(x=9875\) will be calculated as:
super_digit(9875) 9+8+7+5 = 29
super_digit(29) 2 + 9 = 11
super_digit(11) 1 + 1 = 2
super_digit(2) = 2
You are given two numbers \(n\) and \(k\). You have to calculate the super digit of \(P\). \(P\) is created when number \(n\) is concatenated \(k\) times. That is, if \(n=9875\) and \(k=4\), then \(P=9875987598759875\).
SolutionSome observations:
- The super digit of \(P\) is the super digit of the super digit of \(n\) multiplied by \(k\).
- We can recursively calculate the super digit of \(n\) until it has only one digit.
def superDigit(n, k):
# Write your code here
if len(n) == 1:
return int(n)
else:
digit_sum = sum([int(c) for c in n])
return superDigit(str(digit_sum * k), 1)
New Year Chaos
DescriptionIt’s New Year’s Day and everyone’s in line for the Wonderland rollercoaster ride! There are a number of people queued up, and each person wears a sticker indicating their initial position in the queue. Initial positions increment by \(1\) from \(1\) at the front of the line to \(n\) at the back.
Any person in the queue can bribe the person directly in front of them to swap positions. If two people swap positions, they still wear the same sticker denoting their original places in line. One person can bribe at most two others. For example, if \(n=8\) and \(Person 5\) bribes \(Person 4\), the queue will look like this: \(1,2,3,5,4,6,7,8\).
Fascinated by this chaotic queue, you decide you must know the minimum number of bribes that took place to get the queue into its current state!
Examples:
- \(q=[1,2,3,5,4,6,7,8]\) If person \(5\) bribes person \(4\), the queue will look like this: \(1,2,3,5,4,6,7,8\). Only \(1\) bribe is required. Print 1.
- \(q=[4,1,2,3]\) Too chaotic: more than \(2\) bribes required. Print Too chaotic.
Some observations: Let’s consider q=[1, 2, 5, 3, 7, 8, 6, 4]
- Any one can bribe the person directly in front of them to swap positions. So \(P5\) can bribe \(P3\) to swap positions. And this bribe is counted as 1 only.
- \(P8\) can bribe \(P6\) and \(P4\) to swap positions. And this bribe is counted as 2 only.
- Even the \(P4\) is in position 8 at first (i.e., 4 positions away from his correct position), he no need any bribe to get to his correct position. Because along the bribing process of \(P8\) and \(P7\), \(P5\), he will be pushed to his correct position.
- \(P5\) always need to swap positions to $P3\(and\)P4$$ to get to his correct position. The number of bribes for a person is the number of people in front of him that are smaller than him.
So the idea is to find the one in the wrong position and count number of people in front of him that are smaller than him. For example, \(P5\) is in the wrong position and there are 2 people in front of him that are smaller than him, so the total brides for him is 2. The total brides for the whole queue is the sum of brides for each person. The queue is too chaotic if any person in wrong position and located in number less than 2 positions away from his correct position. (Update: This approach is not correct! I will go back to this problem later!)
def minimumBribes(q):
total = 0
is_chaotic = False
for i, n in enumerate(q):
if i+1 != n: # wrong position
sub_total = 0
for j in range(i+1, len(q)):
if q[j] < n:
sub_total += 1
if sub_total > 2:
is_chaotic = True
break
else:
total += sub_total
if is_chaotic:
print('Too chaotic')
else:
print(total)
Another solution is use bubble sort to sort and count the number of swaps. But this solution is not efficient enough to pass the time limit (This method works but slow!)
def minimumBribes(q):
total = 0
is_chaotic = False
count = [0] * len(q)
for i in range(len(q)):
for j in range(len(q)-1):
if q[j] > q[j+1]:
count[q[j]-1] += 1
q[j], q[j+1] = q[j+1], q[j]
total += 1
for c in count:
if c > 2:
is_chaotic = True
break
if is_chaotic:
print('Too chaotic')
else:
print(total)
Truck Tour
DescriptionSuppose there is a circle. There are \(N\) petrol pumps on that circle. Petrol pumps are numbered \(0\) to \((N-1)\) (both inclusive). You have two pieces of information corresponding to each of the petrol pump: (1) the amount of petrol that particular petrol pump will give, and (2) the distance from that petrol pump to the next petrol pump.
Initially, you have a tank of infinite capacity carrying no petrol. You can start the tour at any of the petrol pumps. Calculate the first point from where the truck will be able to complete the circle. Consider that the truck will stop at each of the petrol pumps. The truck will move one kilometer for each litre of the petrol.
Sample Input
3 # N
1 5 # pump 1: petrol, distance
10 3 # pump 2: petrol, distance
3 4 # pump 3: petrol, distance
Clarification:
- Output: An integer which will be the smallest index of the petrol pump from which we can start the tour.
- There is guaranteed to be a unique solution.
Some observations:
- The truck has infinite tank capacity. So it should get petrol at every pump.
- Given the above example, let’s work out each scenario:
- If starting at \(P0\), its petro \(p=1\), while the distance to the next pump is $d=5$. So the truck will run out of petrol at \(P1\). So we can not start at \(P0\).
- If starting at \(P1\), its petro \(10\), \(d=3\). It has \(7\) petrol left after reaching \(P2\). It then loads \(p=P1+P2-d1\) while the distance is \(d2\).
- The petrol will be cummulatively added, if starting from $P0$, at pump $t$-th, the petro is \(p_t=P0 - d0 + P1 - d1 + ... + P_t\), and the condition at each pump is \(p_t \geq d_t\).
- If the truck starts at pump $s$ (shifted), the petro at pump $t$-th is \(p_t=P_s - d_s + P_{s+1} - d_{s+1} + ... + P_{s+t}\), and the condition at each pump is \(p_t \geq d_t\). The condition is satisfied if \(p_t - d_t \geq 0\) for all \(t\)
- We need to compare element-wise of two lists: petro at time $t$ and distance at time $t$. If the petro is always greater than or equal to the distance, then we can start at that pump. The first pump that satisfies the condition is the answer.
def truckTour(petrolpumps):
# Write your code here
n = len(petrolpumps)
petro = []
distance = []
for p, d in petrolpumps:
petro.append(p)
distance.append(d)
petro = petro + petro
distance = distance + distance
for i in range(n):
cum_petro = 0
for j in range(i, i+n):
cum_petro += petro[j] - distance[j]
if cum_petro < 0:
break
if cum_petrol >= 0:
return i
Merge two sorted linked lists
DescriptionYou’re given the pointer to the head nodes of two sorted linked lists. The data in both lists will be sorted in ascending order. Change the next pointers to obtain a single, merged linked list which also has data in ascending order. Either head pointer given may be null meaning that the corresponding list is empty.
Sample Input
1 -> 3 -> 5 -> 6 -> NULL
2 -> 4 -> 7 -> NULL
Sample Output
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> NULL
Solution with recursion:
def mergeLists(head1, head2):
# Write your code here
if head1 is None:
return head2
if head2 is None:
return head1
if head1.data < head2.data:
head1.next = mergeLists(head1.next, head2)
return head1
else:
head2.next = mergeLists(head1, head2.next)
return head2
Solution by iteratively merging two lists:
def mergeLists(head1, head2):
# Write your code here
if head1.data < head2.data:
head = head1
head1 = head1.next
else:
head = head2
head2 = head2.next
current = head
while head1 is not None and head2 is not None:
if head1.data < head2.data:
current.next = head1
head1 = head1.next
else:
current.next = head2
head2 = head2.next
current = current.next
if head1 is None:
current.next = head2
else:
current.next = head1
return head
Queue using Two Stacks
DescriptionA queue is an abstract data type that maintains the order in which elements were added to it, allowing the oldest elements to be removed from the front and new elements to be added to the rear. This is called a First-In-First-Out (FIFO) data structure because the first element added to the queue (i.e., the one that has been waiting the longest) is always the first one to be removed.
A basic queue has the following operations:
- Enqueue: add a new element to the end of the queue.
- Dequeue: remove the element from the front of the queue and return it.
In this challenge, you must first implement a queue using two stacks. Then process \(q\) queries, where each query is one of the following types:
- 1: Enqueue element \(x\) into the end of the queue.
- 2: Dequeue the element at the front of the queue.
- 3: Print the element at the front of the queue.
Pairs
DescriptionYou will be given an array of integers and a target value. Determine the number of pairs of array elements that have a difference equal to a target value.
For example, given an array of \([1, 2, 3, 4]\) and a target value of \(1\), we have three values meeting the condition: \(2-1=1\), \(3-2=1\), and \(4-3=1\).
Solutiondef pairs(k, arr):
# Write your code here
total = 0
valid_dict = dict()
for i in range(len(arr)):
valid_dict[arr[i]] = True
if arr[i] + k in valid_dict:
total += 1
if arr[i] - k in valid_dict:
total += 1
return total
Breadth First Search: Shortest Reach
DescriptionConsider an undirected graph consisting of \(n\) nodes where each node is labeled from \(1\) to \(n\) and the edge between any two nodes is always of length \(6\). We define node \(s\) to be the starting position for a BFS. Given a graph, determine the distances from the start node to each of its descendants and return the list in node number order, ascending. If a node is disconnected, it’s distance should be \(-1\).
For example, there are \(n=5\) nodes in the graph with a starting node \(s=1\). The list of \(edges=[[1,2],[1,3],[3,4]]\), and each has a weight of \(6\).
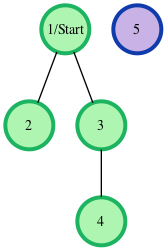
All distances are from the start node \(1\). Outputs are calculated for distances to nodes \(2\) through \(5\): [6,6,12,-1]. Each edge is units, and the unreachable node has the required return distance of \(-1\).
class TreeNode():
def __init__(self, val=-1):
self.val = val
self.children = []
self.visited = False
def bfs(n, m, edges, s):
# Write your code here
# n: number of nodes
# m: number of edges
# edges: list of edges, for example, [[1,2], [1,3], [3,4]]
# s: starting node
# Step 1: Build a graph
graph = dict()
for i in range(n):
graph[i+1] = TreeNode(i+1)
for edge in edges:
graph[edge[0]].children.append(graph[edge[1]])
graph[edge[1]].children.append(graph[edge[0]])
# Step 2: BFS
queue = [graph[s]]
graph[s].visited = True
distance = dict()
distance[s] = 0
while len(queue) > 0:
node = queue.pop(0)
for child in node.children:
if not child.visited:
child.visited = True
queue.append(child)
distance[child.val] = distance[node.val] + 6
result = []
for i in range(1, n+1):
if i != s:
if i in distance:
result.append(distance[i])
else:
result.append(-1)
return result
Tree: Preorder Traversal
DescriptionComplete the preOrder function in your editor below, which has parameter: a pointer to the root of a binary tree. It must print the values in the tree’s preorder traversal as a single line of space-separated values.
SolutionHackerRank provides definition of the tree node and a function to create a tree from a list of values as follows:
class Node:
def __init__(self, info):
self.info = info
self.left = None
self.right = None
self.level = None
def __str__(self):
return str(self.info)
class BinarySearchTree:
def __init__(self):
self.root = None
def create(self, val):
if self.root == None:
self.root = Node(val)
else:
current = self.root
while True:
if val < current.info:
if current.left:
current = current.left
else:
current.left = Node(val)
break
elif val > current.info:
if current.right:
current = current.right
else:
current.right = Node(val)
break
else:
break
Given this setting, we can use recursion to traverse the tree in preorder which is root -> left -> right.
def preOrder(root):
#Write your code here
def _dfs(node):
if node is None:
return
print(node.info, end=' ')
_dfs(node.left)
_dfs(node.right)
_dfs(root)
Tree: Huffman Coding
DescriptionHuffman coding assigns variable length codewords to fixed length input characters based on their frequencies. More frequent characters are assigned shorter codewords and less frequent characters are assigned longer codewords. All edges along the path to a character contain a code digit. If they are on the left side of the tree, they will be a 0 (zero). If on the right, they’ll be a 1 (one). Only the leaves will contain a letter and its frequency count. All other nodes will contain a null instead of a character, and the count of the frequency of all of it and its descendant characters.
For instance, consider the string ABRACADABRA. There are a total of \(11\) characters in the string. This number should match the count in the ultimately determined root of the tree. Our frequencies are \(A=5, B=2, R=2, C=1\) and \(D=1\). The two smallest frequencies are for \(C\) and \(D\), both equal to \(1\), so we’ll create a tree with them. The root node will contain the sum of the counts of its descendants, in this case \(1+1=2\). The left node will be the first character encountered, \(C\), and the right will contain \(D\). Next we have \(3\) items with a character count of \(2\): the tree we just created, the character \(B\) and the character \(R\). The tree came first, so it will go on the left of our new root node. \(B\) will go on the right. Repeat until the tree is complete, then fill in the ‘1’ and ‘0’ values for the edges. The finished graph looks like:
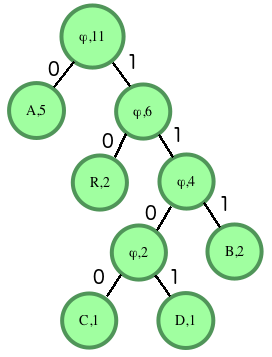
Example:
S="1001011"
Processing the string from left to right.
S[0]='1' : we move to the right child of the root. We encounter a leaf node with value 'A'. We add 'A' to the decoded string.
We move back to the root.
S[1]='0' : we move to the left child.
S[2]='0' : we move to the left child. We encounter a leaf node with value 'B'. We add 'B' to the decoded string.
We move back to the root.
S[3] = '1' : we move to the right child of the root. We encounter a leaf node with value 'A'. We add 'A' to the decoded string.
We move back to the root.
S[4]='0' : we move to the left child.
S[5]='1' : we move to the right child. We encounter a leaf node with value C'. We add 'C' to the decoded string.
We move back to the root.
S[6] = '1' : we move to the right child of the root. We encounter a leaf node with value 'A'. We add 'A' to the decoded string.
We move back to the root.
Decoded String = "ABACA"
It takes quite a bit of time to understand the problem. In the above example, I could not understand why we could know a leaf node with value A there.
Is Possible Path
Description(Canva Coding Challenge for Machine Learning Engineer)
the Problem: Adam is standing at point (a,b) in an infinite 2D grid. He wants to know if he can reach point (x,y) or not. The only operation he can do is to move to point (a+b,b), (a,a+b), (a-b,b), or (a,a-b) from some point (a,b). It is given that he can move to any point on this 2D grid,i.e., the points having positive or negative X(or Y) co-ordinates.
Tell Adam whether he can reach (x,y) or not.
Solutiondef isPossible(a,b,c,d):
def canreach(a, b, c, d):
if a > c or b > d:
return False
if a == c and b == d:
return True
return canreach(a+b, b, c, d) or canreach(a, a+b, c, d)
return 'Yes' if canreach(a, b, c, d) else 'No'
Minimum Area
Description(Canva Coding Challenge for Machine Learning Engineer)
Given a list of \(n\) points in a 2D plane, find the minimum area of a square formed by these points such that at least \(k\) points lie inside the square. The points must be strickly inside the square, means that it cannot lie on a side of the square. The area must be square.
Solutiondef minArea(x, y, k):
# Write your code here
# x: an array of integers
# y: an array of integers
# k: number of points inside the square
# solution: must be a square, not rectangle
def square(bottom_left, side):
# return top_right given bottom_left and side
return [bottom_left[0] + side, bottom_left[1] + side]
def count_points_inside(x, y, top_right, bottom_left):
# check whether it is a square
count = 0
for px, py in zip(x, y):
if (px > bottom_left[0]) and (px < top_right[0]) and (py > bottom_left[1]) and (py < top_right[1]):
count += 1
return count
# init the square with bottom_left at min(x), min(y)
bottom_left = [min(x)-1, min(y)-1]
side = max(max(x) - min(x), max(y) - min(y)) + 2
# side = 1
top_right = square(bottom_left, side)
stop = False
while not stop:
points_inside = count_points_inside(x, y, top_right, bottom_left)
if points_inside >= k:
side -= 1
top_right = square(bottom_left, side)
else:
stop = True
return (side+1) * (side+1)
This solution can not pass the time limit! It is because of the count_points_inside function which is not leveraged the previous result to reduce the time. The better solution is using binary search
# Write your code here
# x: an array of integers
# y: an array of integers
# k: number of points inside the square
# solution: must be a square, not rectangle
def square(bottom_left, side):
# return top_right given bottom_left and side
return [bottom_left[0] + side, bottom_left[1] + side]
def count_points_inside(x, y, top_right, bottom_left):
# check whether it is a square
count = 0
for px, py in zip(x, y):
if (px > bottom_left[0]) and (px < top_right[0]) and (py > bottom_left[1]) and (py < top_right[1]):
count += 1
return count
# init the square with bottom_left at min(x), min(y)
bottom_left = [min(x)-1, min(y)-1]
side_max = max(max(x) - min(x), max(y) - min(y)) + 2
side_min = 1
side_mid = (side_max + side_min) // 2
top_right = square(bottom_left, side_mid)
valid_side = []
# Binary search
while side_min < side_max:
points_inside = count_points_inside(x, y, top_right, bottom_left)
if points_inside >= k:
valid_side.append(side_mid)
# reduce the size of square
side_max = side_mid
else:
side_min = side_mid + 1
side_mid = (side_max + side_min) // 2
top_right = square(bottom_left, side_mid)
return min(valid_side) * min(valid_side)
Enjoy Reading This Article?
Here are some more articles you might like to read next: