Stanford CS231N | Spring 2025 | Lecture 8- Attention and Transformers
- Lecture overview: attention and transformers
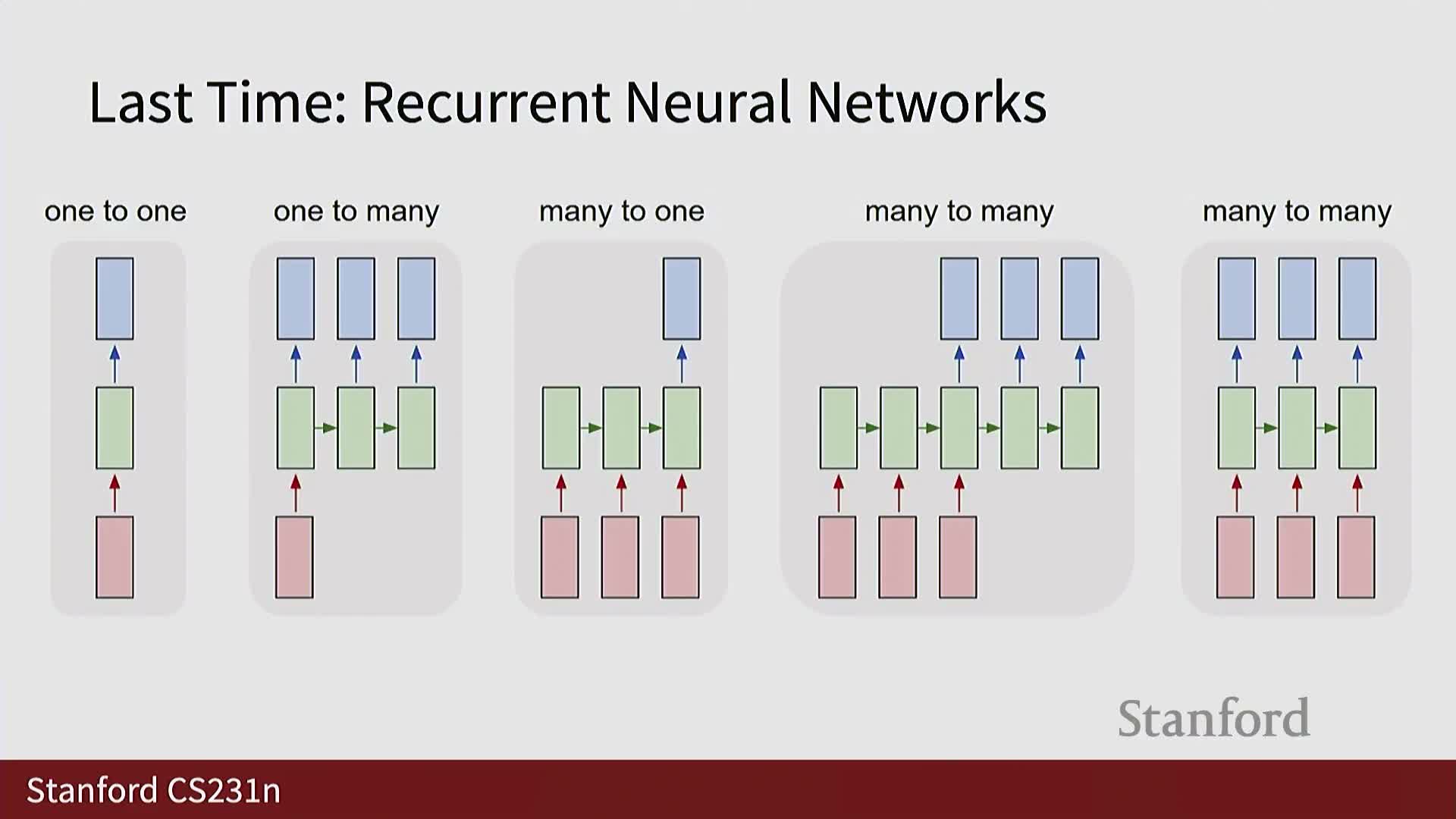
- Historical motivation: self-attention grew from recurrent neural networks
- Sequence-to-sequence translation with encoder-decoder RNNs
- Bottleneck limitation of fixed-length context vectors
- Attention within RNNs: alignment scores, softmax, and context vectors
- Training, differentiability and decoder initialization with attention
- Iterative attention across decoder time steps solves the bottleneck
- Interpreting attention via attention weight visualizations and alignment matrices
- Abstracting attention: queries, data (keys/values) and output context vectors
- Scaled dot-product similarity and the need to normalize by sqrt(d)
- Batch computation of attention via matrix multiplies for multiple queries
- Keys and values: separating matching and retrieved content
- Self-attention: projecting each input to queries, keys, and values and efficient fused computation
- Permutation equivariance, positional embeddings, and masking for autoregressive tasks
- Multi-headed self-attention and its batched implementation
- Comparing sequence-processing primitives: RNNs, convolutions, and self-attention
- Transformer architecture: layers, residuals, layernorm, MLPs, stacking and applications
Lecture overview: attention and transformers
This lecture introduces attention as a neural-network primitive that operates on sets of vectors and presents the transformer architecture, which places self-attention at its core.
It frames transformers as the dominant, general-purpose architecture used across large-scale deep learning for language, vision, audio, and multimodal tasks.
The segment provides historical context: self-attention evolved from ideas developed around recurrent neural networks (RNNs) and previews a roadmap that moves from RNN-based translation → attention → full transformer architectures.
Practically, this matters because transformers are the basis for most state-of-the-art large models deployed in production today.
Historical motivation: self-attention grew from recurrent neural networks

Self-attention and transformer ideas are motivated by prior work on recurrent neural networks; the historical development explains why attention arose naturally when addressing limitations of encoder–decoder RNNs.
Key points:
- Attention ideas were developing for years prior to the invention of the transformer, not invented in isolation.
- Understanding RNN-based sequence processing helps motivate why attention was a necessary architectural step.
- This segment sets the stage for rolling back to RNN seq2seq translation to concretely motivate the attention mechanism.
Sequence-to-sequence translation with encoder-decoder RNNs
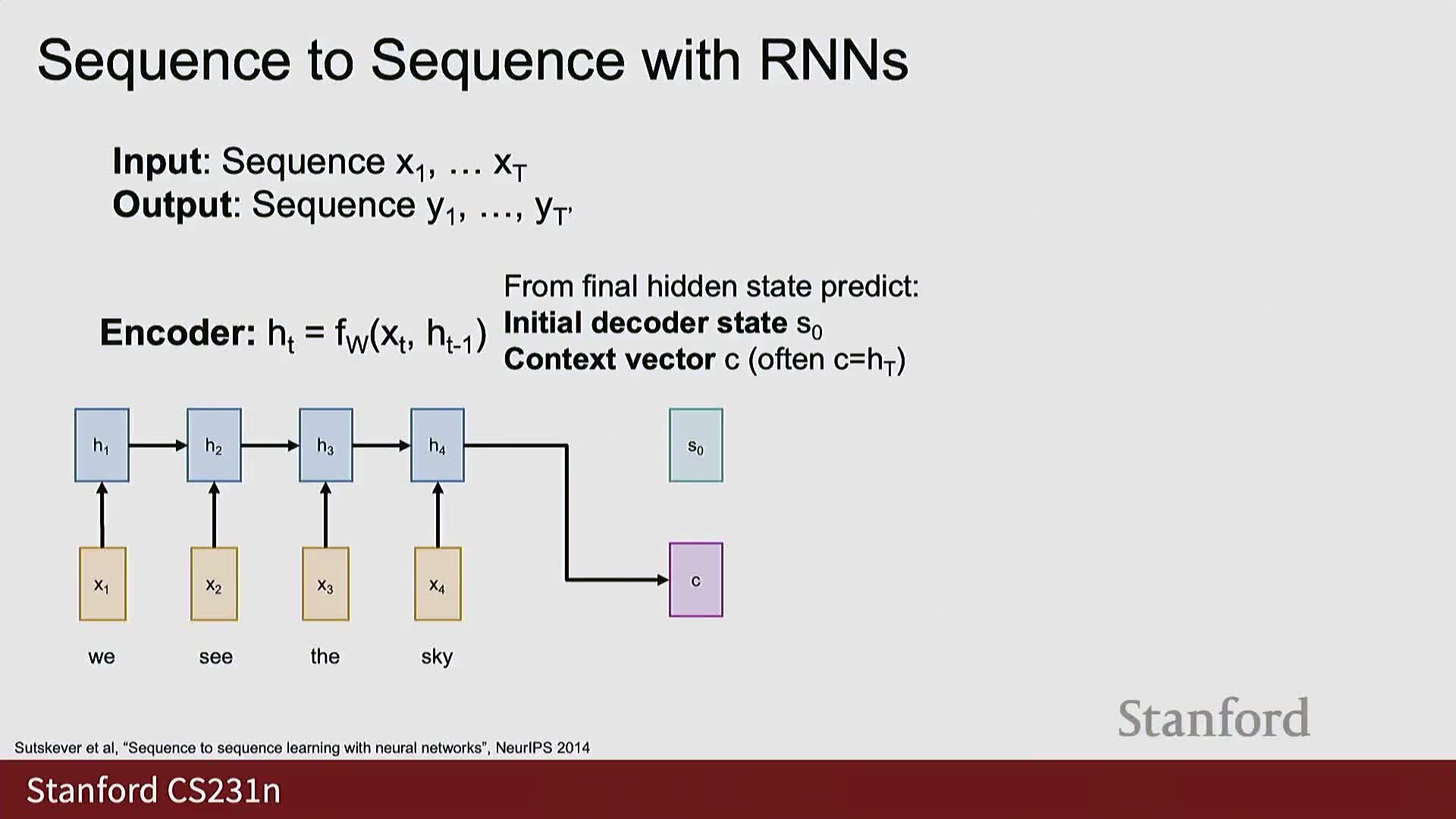
Sequence-to-sequence (seq2seq) translation is modeled with two main components:
-
Encoder RNN
- Consumes the source token sequence sequentially.
- Produces a sequence of hidden states.
- Typically summarizes the entire input into a single fixed-length context vector (often the final encoder hidden state).
-
Decoder RNN
- Generates the target token sequence one step at a time.
- Conditions each output on: the previous output token, its previous hidden state, and the fixed context vector from the encoder.
This formulation naturally handles variable-length input and output sequences by letting the encoder compress input information and the decoder generate outputs conditioned on that summary.
Bottleneck limitation of fixed-length context vectors

Encoding an entire input sequence into a single fixed-size context vector creates a communication bottleneck between encoder and decoder that worsens as input length or complexity grows.
Problems caused by the bottleneck:
-
Fixed dimensionality forces the same number of floats to represent short phrases and long paragraphs alike.
- This is impractical for long sequences and limits representational capacity.
- Important details can be lost when everything must pass through one vector.
The segment motivates an architectural change: allow the decoder to flexibly access encoder internal representations during decoding rather than forcing all information through one vector.
Attention within RNNs: alignment scores, softmax, and context vectors
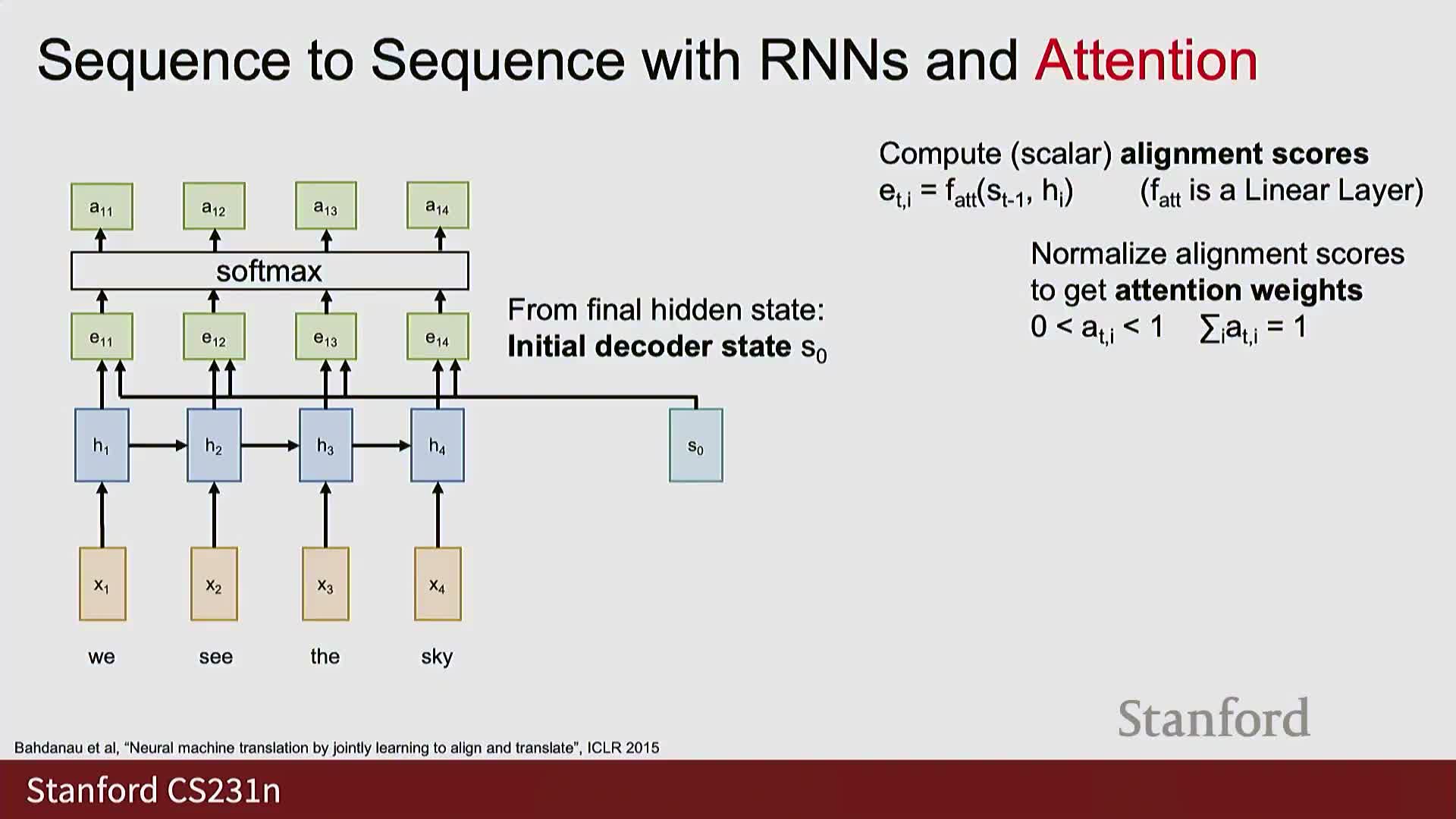
Attention augments the encoder–decoder RNN by computing alignment between the current decoder state and each encoder hidden state and using that to form a context vector specific to the decoder time step.
Mechanism (high level):
- Compute scalar alignment scores between the current decoder state and each encoder hidden state using an alignment function f_a (commonly a small feedforward layer or a dot-product variant).
- Convert those scores to a probability distribution with softmax, producing attention weights.
- Form a weighted linear combination of encoder hidden states using those weights to produce the time-step-specific context vector supplied to the decoder.
This produces a context vector tailored to each decoder step, enabling the model to dynamically attend to the most relevant parts of the input.
Training, differentiability and decoder initialization with attention

The attention mechanism is fully differentiable and trained end-to-end with the same cross-entropy loss used for seq2seq learning, so alignment patterns are learned automatically without supervised alignments.
Decoder initialization is an orthogonal design choice and common options include:
-
Zeros for the initial hidden state.
- The encoder’s final hidden state.
- A learned projection from the encoder final state.
The model adapts during training to whichever initialization is used. The decoder RNN otherwise continues to operate as before, except its context vector is now computed via attention rather than a fixed summary.
Iterative attention across decoder time steps solves the bottleneck
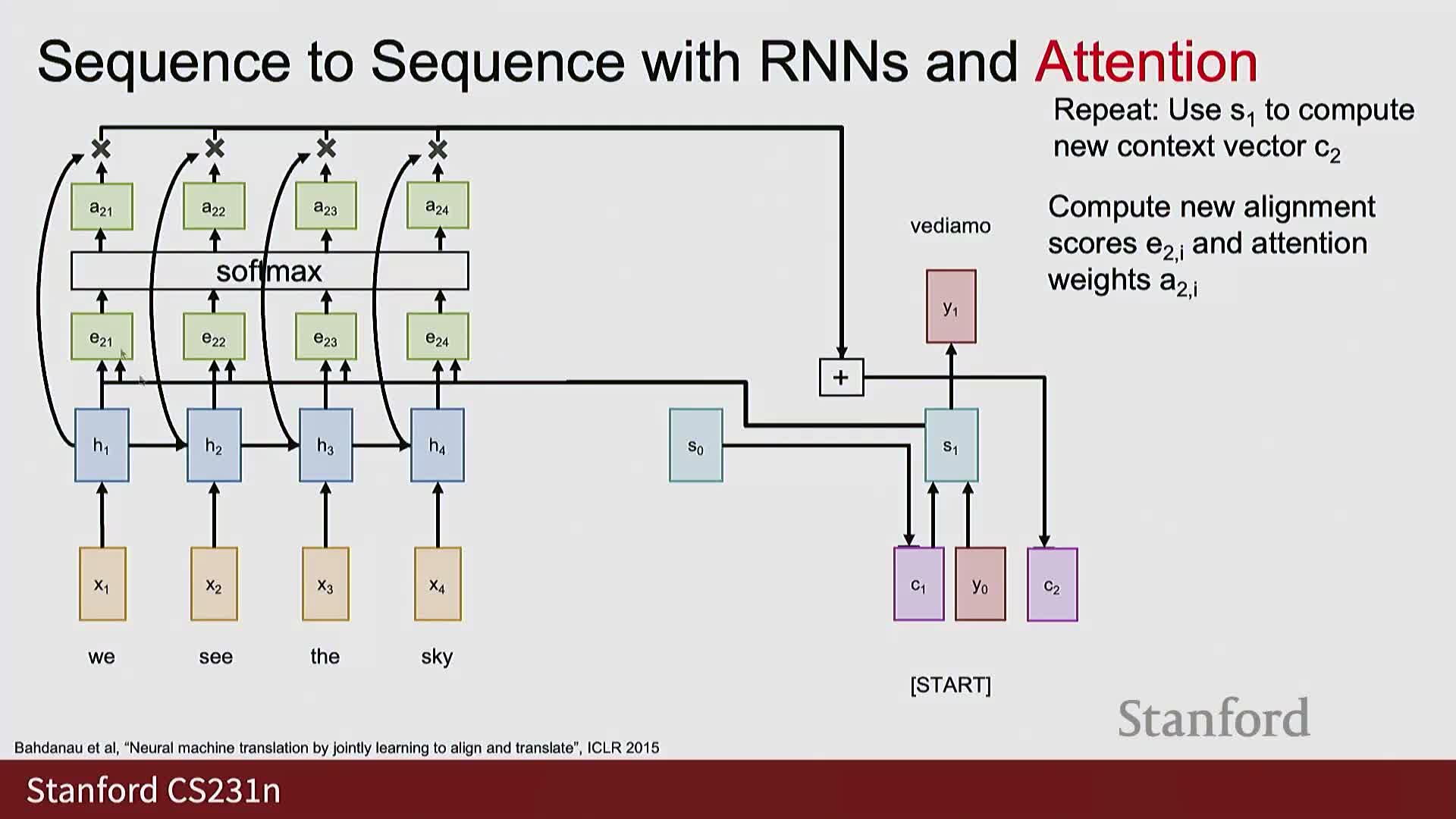
At every decoder time step the model recomputes attention weights using the current decoder state, forms a new context vector from the encoder states, and uses that context to produce the next decoder hidden state and output token.
Consequences and benefits:
- This removes the fixed-length bottleneck.
- Repeating the process for each output token enables the decoder to look back at the entire input sequence as needed.
- The model scales better to long inputs and yields improved alignment for translation and other seq2seq tasks.
The mechanism preserves sequential decoding while enabling flexible, per-step access to encoder representations.
Interpreting attention via attention weight visualizations and alignment matrices

Attention weights can be visualized as a matrix showing the distribution over input positions for every output token.
Observations from such visualizations:
- Often reveal diagonal patterns for monotonic alignments.
- Show more complex patterns for reordering or many-to-many correspondences.
- Provide interpretable insight into what the model focuses on when producing each output token.
Empirically, models often discover sensible alignments and grammar-like reorderings without explicit supervision—this was demonstrated in the seminal 2015 neural machine translation work that established the attention-based alignment-and-translate approach.
Abstracting attention: queries, data (keys/values) and output context vectors

Attention can be abstracted into a standalone operator that maps query vectors and a set of data vectors to output context vectors by computing similarities, normalizing them, and forming weighted sums.
Conceptual view:
- Each query asks: “what information do I need from the data vectors?”
- The attention operator returns a data-dependent linear combination (the context vector) of the data vectors.
- This divorces attention from RNN control flow and makes it a reusable layer.
Roles clarified in the operator view:
-
Queries: drive what to retrieve.
-
Keys: derived from data, compared against queries to produce weights.
-
Values: derived from data, combined using the weights to produce outputs.
Scaled dot-product similarity and the need to normalize by sqrt(d)

A practical and efficient similarity function for attention is the scaled dot product between query and key vectors, where the raw dot product is divided by the square root of the key/query dimensionality (sqrt(d)).
Why scale by sqrt(d)?
- Prevents excessively large inner products as dimensionality increases.
- Without scaling, large magnitudes push the softmax into sharp regimes that can cause vanishing gradients and poor learning.
Using the scaled dot product yields numerically stable attention distributions across a wide range of model sizes and is standard in modern transformer-style attention.
Batch computation of attention via matrix multiplies for multiple queries

When processing multiple queries against multiple data vectors, attention computes all pairwise (scaled) dot-product similarities efficiently as a single matrix multiply between Q and K^T, applies softmax across the appropriate axis to produce attention weight matrices, and computes outputs as a matrix multiply between the attention weights and the V matrix.
This batched formulation is both computationally efficient and hardware-friendly:
- Enables parallel computation of all queries in one operation.
- Leverages optimized BLAS/GEMM kernels on GPUs and TPUs.
- Reduces attention to a small number of large matrix multiplies plus elementwise softmax operations.
Keys and values: separating matching and retrieved content
To decouple how data vectors are matched from what information is returned, each data vector is projected into a key vector (used for matching with queries) and a value vector (used for constructing outputs); both projections are learned linear transforms.
Analogy and role separation:
-
Query expresses what is being sought.
-
Key is the indexable matching representation.
-
Value is the retrieved payload combined by the attention weights.
Keys and values are learned jointly as model parameters, enabling flexible matching and retrieval behavior.
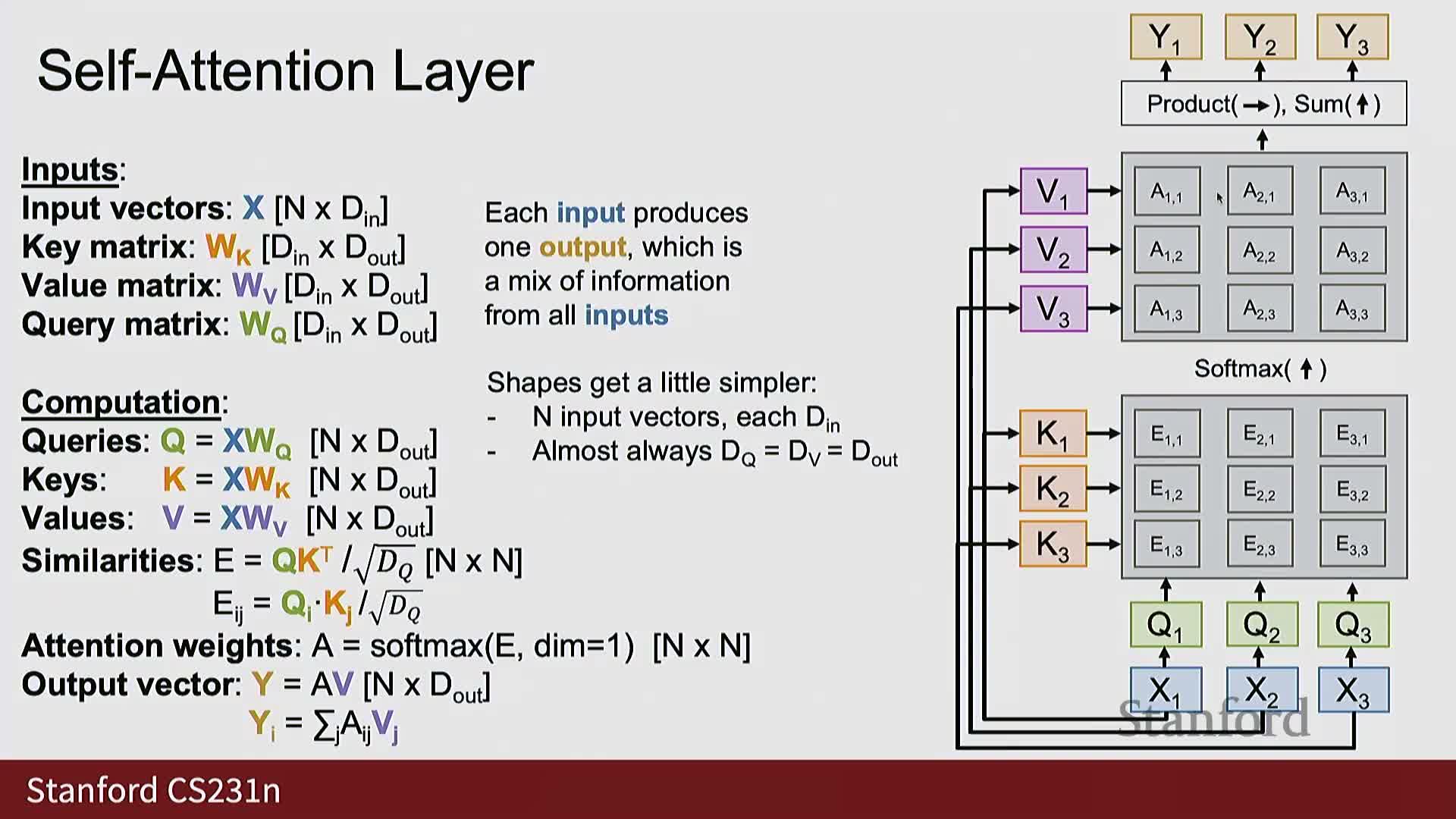
Self-attention: projecting each input to queries, keys, and values and efficient fused computation
Self-attention is a specialization where the same single set of input vectors is projected into queries, keys, and values (one projection per role) and each input position attends to every other position.
Implementation notes:
- The three projections can be computed efficiently with a single fused QKV matrix multiply that produces concatenated Q, K, V tensors.
- These tensors are reshaped and processed with batched matrix multiplies and softmax to compute outputs.
Architectural hyperparameters include input/output dimensionality and per-head dimensions; in practice Din and Dout are often the same and computing fused QKV is more efficient on modern hardware.
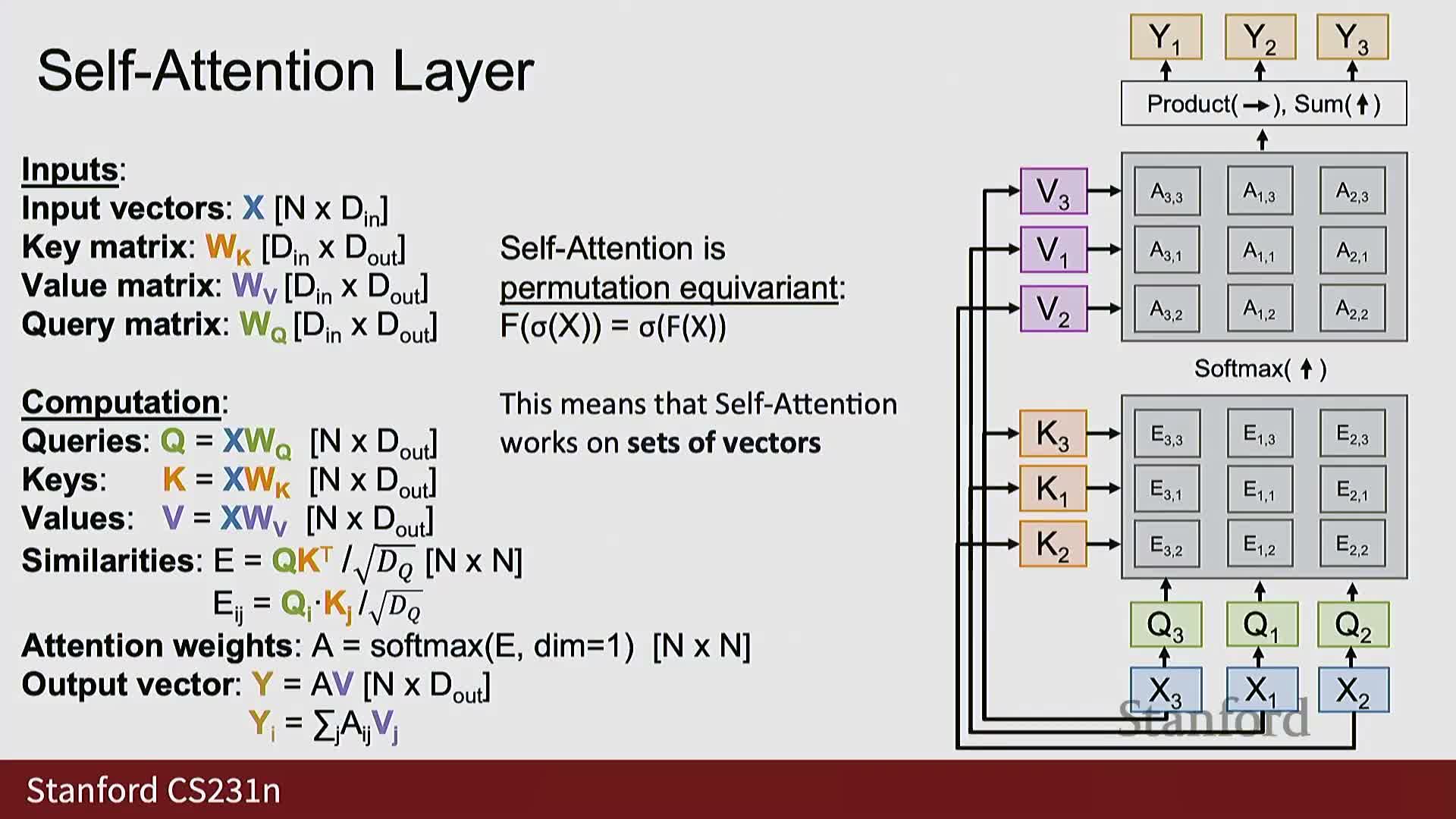
Permutation equivariance, positional embeddings, and masking for autoregressive tasks

A pure self-attention layer is permutation-equivariant: shuffling the input rows produces identically shuffled outputs, so the layer by itself does not encode absolute order.
To incorporate order for sequence tasks:
- Add or append positional embeddings to inputs so the model can distinguish positions.
- For autoregressive language modeling use masked self-attention: set attention logits for forbidden future positions to negative infinity so the softmax yields zero weight, preventing the model from “looking ahead” and ensuring causality.
Multi-headed self-attention and its batched implementation
Multi-headed attention runs multiple independent attention “heads” in parallel, each with distinct projection matrices, allowing the model to attend to different subspaces and capture diverse patterns.
Mechanics and benefits:
- Head outputs are concatenated and linearly projected to fuse information.
- The design increases capacity and expressivity while remaining implementable with batched matrix multiplies: fused QKV projection, batched QK^T similarity, batched attention-weighted value aggregation, and a final output projection.
Multi-head attention is the practical default in transformer implementations because it balances richer representation with parallelizable computation.
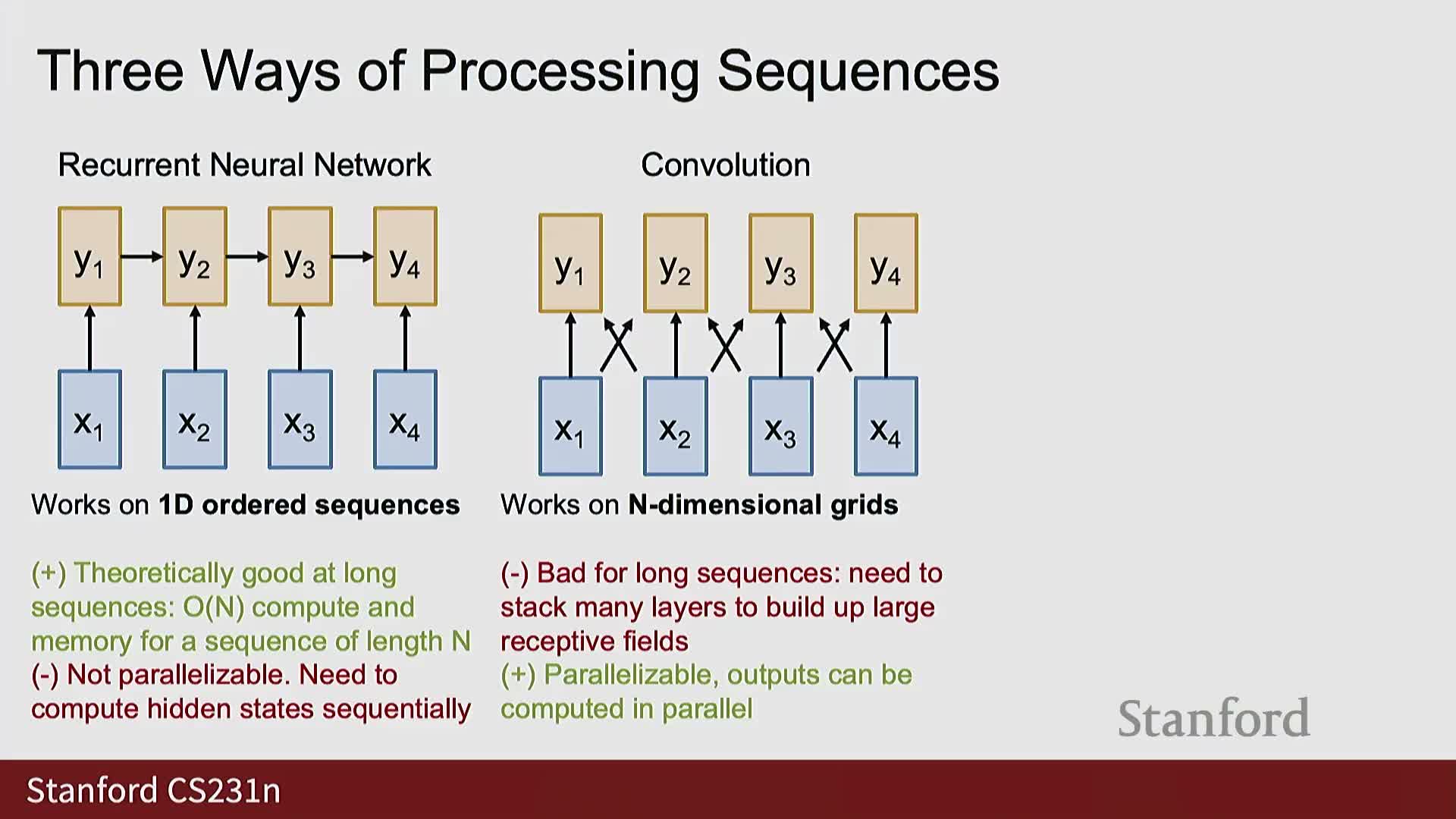
Comparing sequence-processing primitives: RNNs, convolutions, and self-attention

Compare architectural families for sequence modeling:
-
Recurrent Neural Networks (RNNs)
- Process ordered 1D sequences sequentially with inherent temporal dependency.
- Hard to parallelize across time steps, which limits scale.
-
Convolutions
- Operate on n-dimensional grids and are parallelizable.
- Usually require deep stacks or large kernels to achieve large receptive fields, which can reintroduce sequential depth.
-
Self-attention
- Operates on sets of vectors with global pairwise interactions computed in a single layer.
- Highly parallelizable because it reduces to matrix multiplies.
- Naturally scales to long-range dependencies, at the cost of O(n^2) compute and memory for sequence length n.
This trade-off has proven effective when ample hardware parallelism is available.
Transformer architecture: layers, residuals, layernorm, MLPs, stacking and applications
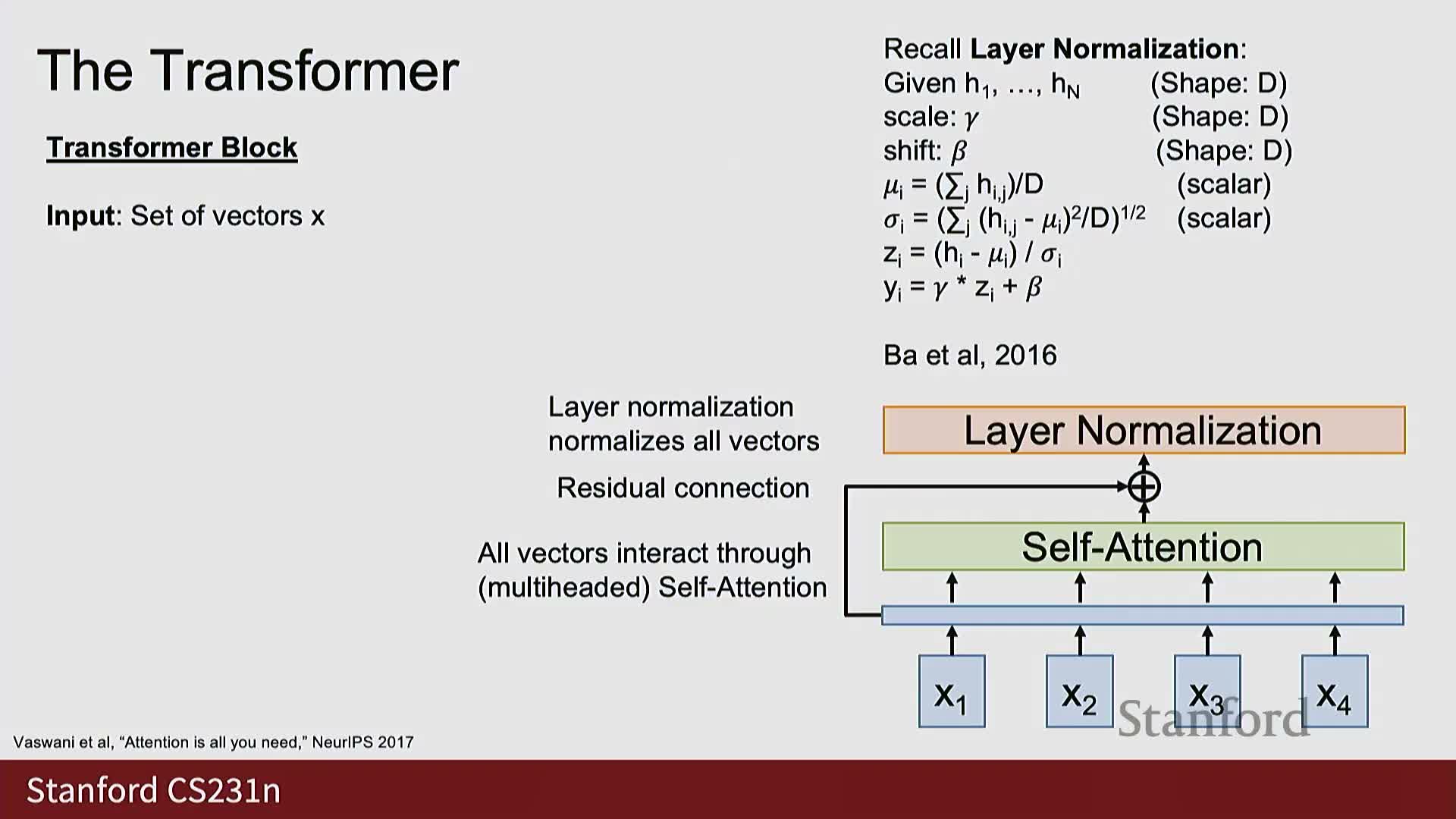
The transformer composes repeated transformer blocks; each block typically performs the following sequence:
-
Multi-headed self-attention
- Add a residual connection and apply layer normalization
- Apply a position-wise feedforward network (FFN / MLP)
- Add another residual and layer normalization
Design rationale:
- Combines global interaction (self-attention) with per-position nonlinear processing (FFN).
- Stacking many such blocks yields powerful hierarchical models.
-
Residuals and layernorm improve gradient flow and training stability.
Transformers scale from tens to hundreds of layers and from millions to trillions of parameters, can be adapted to vision by tokenizing image patches into vectors, and are now the dominant architecture for large-scale models across modalities.
Enjoy Reading This Article?
Here are some more articles you might like to read next: