mindmap Optimize LM primitives on GPU GPU architecture & execution SMs · registers · shared memory Memory hierarchy · warps · waves Maximize arithmetic intensity Measure & profile workflow Warm-ups · trials · synchronize Coarse benchmarks + fine profiling NVTX / Nsight to see queuing Toolchain & implementations Hand-tuned CUDA → PTX inspection Triton block-centric kernels torch.compile / JIT fusion first Kernel fusion & memory traffic Fuse elementwise GELU, softmax Reduce DRAM passes & launches In-register reductions for stability Kernel design patterns Grid/block/warp index pattern Masked/vectorized loads · block size Keep temporaries in registers/shared Optimization priorities GEMMs usually dominate composites Fuse non-GEMM elementwise paths Profile → prefer JIT → custom only if needed

Lecture plan for GPU performance work on language-model components

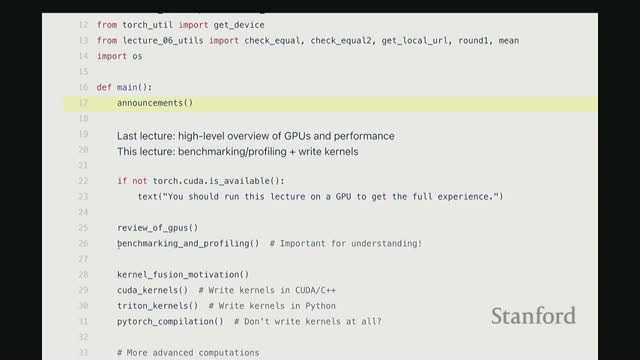
The lecture outlines a practical course segment focused on writing high-performance GPU code for language-model primitives using multiple approaches.

Key objectives for students:

  • Profile code to find real bottlenecks.
  • Implement a Triton kernel for FlashAttention.
  • Write CUDA kernels in C++ and inspect generated PTX to understand low-level GPU behavior.
  • Compare custom kernels against PyTorch’s JIT-compiled implementations.
  • Benchmark, profile, and iteratively optimize common components (e.g., softmax, GLU) in preparation for Assignment 2.

Emphasis:

  • Empirical, side-by-side comparison of implementations.
  • Understanding the hardware- and assembly-level implications of kernel designs.

GPU architecture essentials: SMs, memory hierarchy, thread blocks, warps, and waves

  • GPU architecture is organized into streaming multiprocessors (SMs) that contain many arithmetic units and a large register file for per-thread temporaries.
  • The memory hierarchy ranges from large, high-latency global DRAM down to caches, on-SM shared memory, and registers (small, low-latency). Minimizing DRAM traffic and exploiting registers/shared memory is critical for performance.
  • Parallel execution is hierarchical:
    • A grid of thread blocks is scheduled onto SMs.
    • Each block contains many threads.
    • Threads execute in groups of 32 called warps, the hardware scheduling granularity.
  • Performance considerations:
    • Balance work across warps and blocks to improve utilization.
    • Arithmetic intensity (flops per byte moved) must be maximized to avoid memory-bound behavior.
    • Well-tuned GEMM is typically compute-bound; many other kernels become memory-bound without careful fusion or tiling.

Benchmarking and profiling are prerequisites for targeted GPU optimization

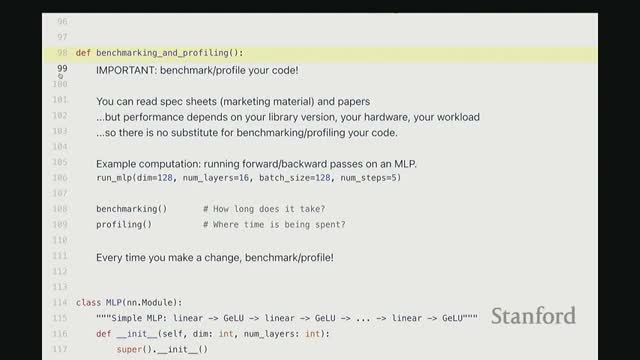
Effective GPU optimization starts with two complementary activities:

  1. Coarse-grain benchmarking — measure end-to-end wall-clock time to understand steady-state throughput.
  2. Fine-grain profiling — inspect kernel launches, library calls, and synchronization to locate hotspots and CPU-side overheads.

Why both matter:

  • Benchmarking captures real performance under representative loads and exposes scaling behavior.
  • Profiling reveals where time is spent (dominant kernels, dispatch/launch costs, synchronization), which guides whether to hand-write kernels, use Triton, or rely on a JIT.
  • Without empirical measurement, optimization effort is often misdirected.

How to implement robust GPU benchmarking: warm-ups, trials, and synchronization

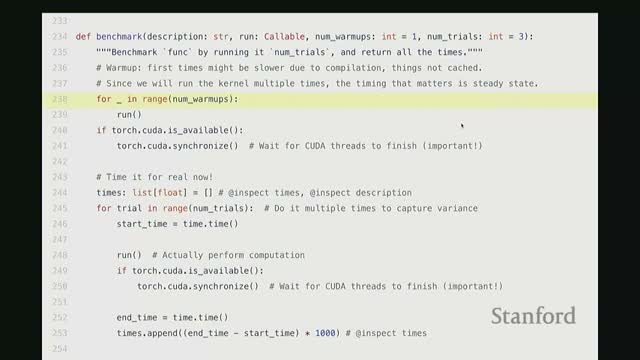
A correct GPU benchmarking wrapper should follow a reproducible pattern:

  1. Run several warm-up iterations so JIT compilation and device initialization finish before timing.
  2. Execute multiple timed trials to reduce noise from system variability and thermal effects.
  3. Call torch.cuda.synchronize() before and after measured regions so the CPU waits for GPU completion and timings reflect GPU work.
  4. Aggregate results (average, median, or distribution) to report robust runtime estimates.

Usage example (conceptual): benchmark a representative MLP with fixed dimensions, layers, batch-size, and repeated forward/backward steps to compare implementations and scaling behavior.

Empirical scaling of matrix multiply and MLP workloads reveals overheads and linear relationships

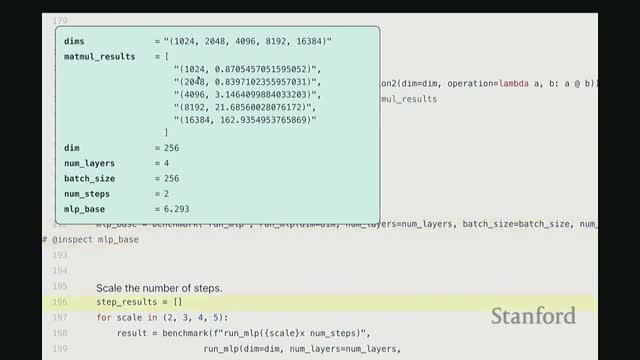
  • Matrix multiply timings grow predictably with matrix size, but at small sizes runtimes are dominated by fixed overheads (kernel launch, CPU–GPU transfer, small-matrix code paths).
  • Once matrices are large enough, runtimes follow expected compute scaling.
  • For a stacked Linear + GLU MLP:
    • End-to-end runtime scales approximately linearly with the number of forward/backward steps.
    • Runtime also scales roughly linearly with the number of layers, indicating per-layer costs aggregate predictably.
  • Benchmarking these scalings helps decide where to focus optimization (large GEMMs vs per-layer elementwise overhead).

Profilers expose low-level CUDA activity behind PyTorch calls, including kernel launches and synchronization

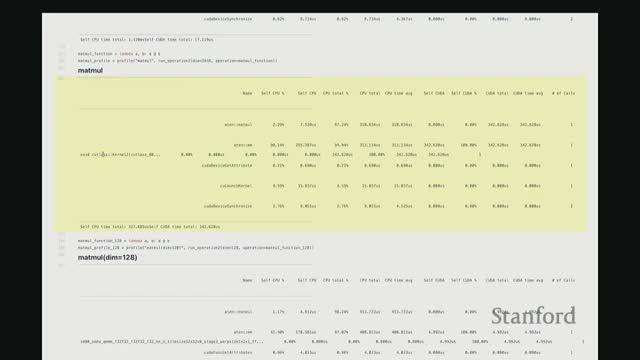
A profiler reveals how high-level PyTorch ops map down the stack:

  • High-level ops dispatch to lower-level AOT/C++ wrappers and specific CUDA kernels (elementwise/vectorized kernels, GEMM primitives).
  • CPU-side costs include cuLaunchKernel overhead and cudaDeviceSynchronize wait time.

Example cases identified by profiling:

  • A no-op sleep shows primarily device synchronization costs.
  • An elementwise add maps to a vectorized elementwise kernel plus an A10 C interface wrapper.
  • GEMM dispatches to cuBLAS/cuTensile kernels tuned for specific tile sizes and hardware.

Caveats:

  • Profilers add overhead and can perturb microsecond-scale timings, but they reliably identify dominant GPU kernels and CPU-side dispatch/launch costs.

Composite primitives like cdist decompose into GEMMs, elementwise ops, and copies with GEMM typically dominating

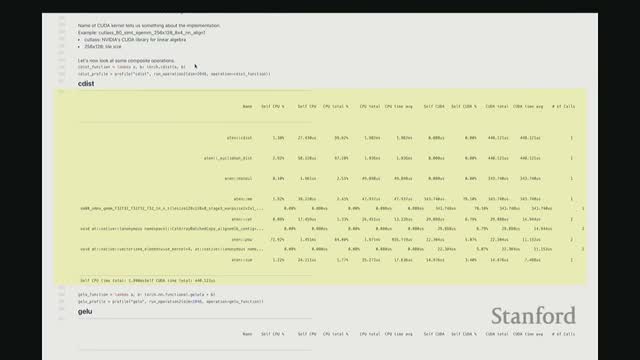
Computing pairwise Euclidean distances (cdist) decomposes into linear-algebra primitives:

  • GEMM operations for dot-products.
  • Elementwise power operations and sums.
  • Copies/concatenations for assembling outputs.

Profiling a composite cdist shows:

  • GEMMs often consume the majority of GPU time (e.g., ~70–80%).
  • Copies and elementwise kernels consume smaller percentages.

Implication:

  • Accelerating or selecting the best GEMM implementation yields the largest payoff for cdist-style computations.

Fused implementations exist for key nonlinearities such as GELU and softmax to minimize memory traffic and launch overhead

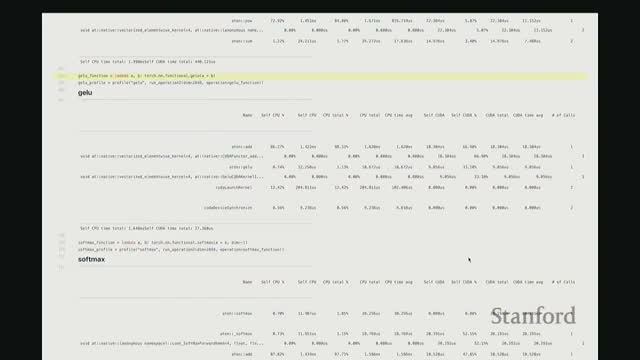
  • Nonlinearities used in language models—GELU and softmax—are typically implemented as fused CUDA kernels that combine multiple arithmetic steps into one device pass.
  • GELU is a composition of operations (often approximated via polynomial or tanh-based forms) and benefits from evaluating the full expression in registers to avoid intermediate global-memory writes.
  • Softmax requires reductions and numerically stable exponentiation: fused kernels subtract the row-wise max, exponentiate, reduce sums, and divide in a single pass.
  • Using fused operators reduces DRAM traffic and kernel-launch overhead, significantly improving throughput versus composing separate primitive kernels.

CPU and GPU execute asynchronously; NVTX annotations and Nsight timelines reveal queueing, synchronization points, and the effect of CPU-side operations

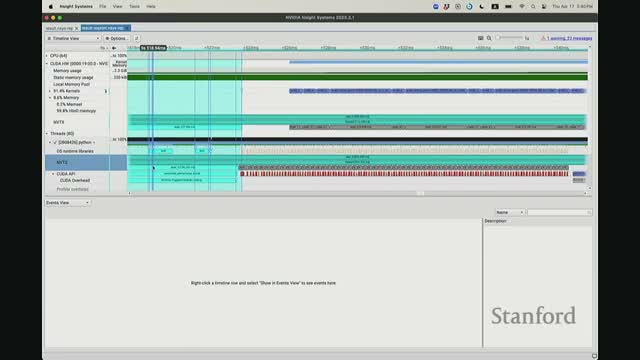
  • The CPU dispatches CUDA kernels asynchronously and can enqueue many kernels ahead of GPU execution up to a hardware/driver queue depth.
  • Nsight and NVTX annotations make that queueing visible by mapping CPU code ranges to GPU events in hardware timelines.
  • If the CPU issues a host-side operation that requires a GPU result (e.g., printing a loss), the code must synchronize, forcing the CPU to wait and changing pipeline/queue behavior.
  • Annotating code with NVTX and inspecting CUDA hardware timelines in NVIDIA Nsight helps understand initialization overheads, command queue depth, kernel ordering, and where CPU-side synchronization causes stalls or reduces concurrency.

Kernel fusion concept: fuse multiple elementwise ops into one kernel to reduce repeated memory movements

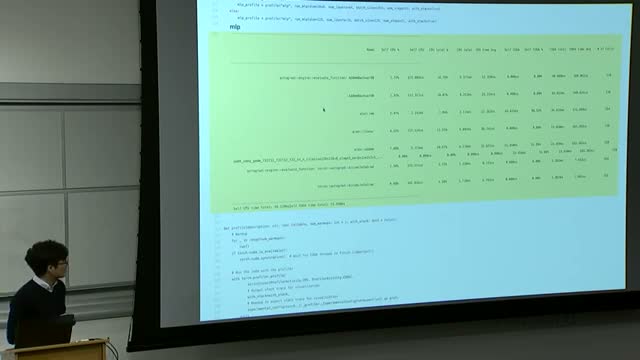
Kernel fusion consolidates sequential elementwise operations into a single GPU kernel so intermediate results remain in registers or shared memory rather than being written to and re-read from global DRAM.

Benefits of fusion:

  • Fewer kernel launches.
  • Reduced global memory bandwidth usage.
  • Increased arithmetic intensity.
  • Often yields order-of-magnitude improvements on elementwise-heavy code paths.

Fusion is a critical optimization for non-GEMM portions of language models where memory traffic otherwise dominates.

A naive PyTorch elementwise GELU implementation issues many kernels and is much slower than a fused implementation

  • Writing GELU as a sequence of PyTorch operations (constants, multiply, tanh, power, additions) produces multiple separate kernels.
  • Each kernel performs a full pass over the tensor, causing repeated DRAM reads/writes plus launch overhead.
  • Benchmarking shows the naive multi-kernel PyTorch sequence is significantly slower (several-fold) than a single fused kernel that evaluates the same algebra in one pass.

Conclusion: this motivates implementing fused kernels in CUDA, Triton, or relying on JIT-based fusion to reclaim performance.

How a custom CUDA kernel implements fused elementwise computation using the grid/block/thread model

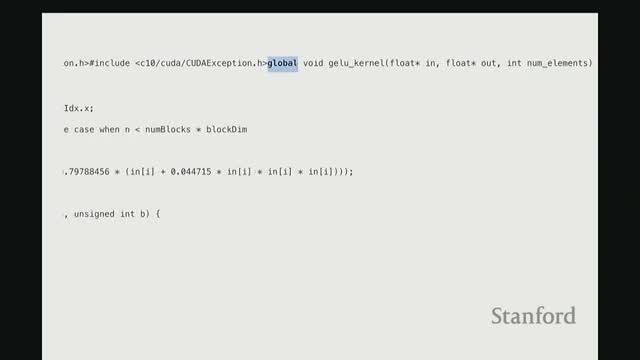
A CUDA kernel typically comprises three components:

  1. A host-side wrapper that prepares inputs/outputs and computes launch parameters.
  2. A __global__ kernel function that executes on the device.
  3. A launch configuration specifying grid and block dimensions.

Kernel coding pattern:

  • Compute a global index: I = blockIdx.x * blockDim.x + threadIdx.x and check bounds (I < num_elements).
  • Perform pointer-based loads into registers, compute the fused expression in registers, and store results back to global memory.
  • Efficient practices: allocate outputs with torch.empty_like to avoid unnecessary initialization, choose block sizes to saturate SMs, and use synchronous launches during debugging.

Example impact: a fused CUDA GELU kernel reduced measured runtime from ~8 ms (naive) to ~1.8 ms in the example.

Triton DSL: block-centric vectorized GPU programming in Python that emits PTX

  • Triton is a Python-based domain-specific language that expresses GPU kernels at the thread-block level while abstracting thread management, memory coalescing, and shared-memory use.
  • Authors program in terms of blocks and vectorized offsets: each block computes a contiguous vector of offsets, performs masked/coalesced loads, computes on those vectors (keeping temporaries in registers), and stores results back.
  • The Triton compiler generates efficient PTX (showing grouped LDs that load multiple lanes and fused floating-point sequences), enabling rapid development of fused kernels.
  • In many cases, Triton delivers performance comparable to hand-written CUDA while dramatically reducing development effort.

Torch.compile JIT can automatically fuse operations and emit Triton kernels to approach or exceed hand-written kernels for many primitives

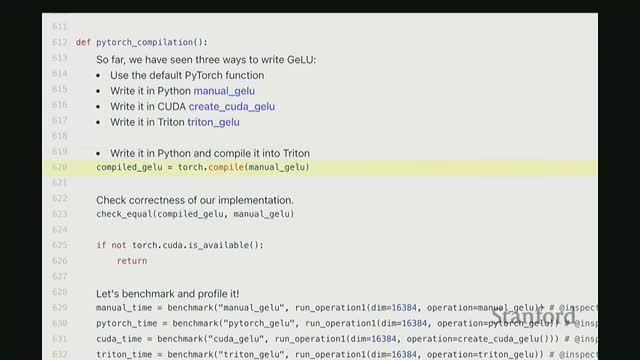
  • Modern JIT compilers (e.g., torch.compile) perform end-to-end transformations that include operation fusion and microbenchmark-driven selection of optimal GEMM subroutines for the target device.
  • torch.compile can generate Triton kernels under the hood to fuse elementwise sequences and pick high-performance implementations for matrix multiplications.
  • For many workloads, JIT-generated code achieves performance close to or better than manually written Triton/CUDA.
  • Caveat: highly specialized routines (e.g., recent FlashAttention variants exploiting specific hardware features) may still benefit from hand-tuned kernels.

Recommended workflow: rely on JIT/fusion for most cases and reserve custom kernels for uniquely constrained hotspots identified by profiling.

Softmax in Triton: handle reductions by assigning rows to blocks, using vectorized loads, computing max/exponentials/sum, and writing normalized outputs

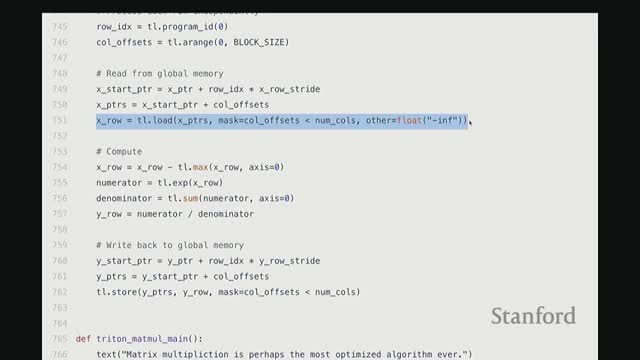
Row-wise softmax requires a reduction across the row; a common Triton design maps one block per row so the block can load columns into lanes and compute a numerically stable softmax in-block:

  1. Subtract the row max (numerical stability).
  2. Exponentiate the shifted values.
  3. Reduce to a sum.
  4. Divide to normalize.

Triton implementation details:

  • Use next_power_of_two to pick convenient block sizes.
  • Use masked loads to handle tail elements.
  • Use vectorized LD/STs to exploit memory coalescing.

Benchmarking observations:

  • Naive multi-pass implementations are slow due to repeated DRAM access and multiple kernels.
  • Fused compiled / PyTorch / Triton softmax kernels substantially reduce kernel-launch and memory costs, yielding much faster per-row softmax performance.