This lecture presents case studies of scaling laws in modern large language model development and a mathematical deep dive into Maximum Update Parameterization (MUP).

The lecture frames two primary goals: to examine detailed case studies of how contemporary LLM builders apply scaling laws in practice, and to present a mathematical treatment of Maximum Update Parametrization (MUP) that makes hyperparameters scale-invariant.

It highlights common practitioner concerns about scaling-law use, including whether log–log curve fits reliably predict optimal token/model trade-offs and hyperparameters such as learning rate.

Motivation and approach:

  • Study both published scaling-law analyses and less-documented industrial practices to derive best practices for model sizing, data budgets, and stable training parameterizations.
  • Use case studies (Cerebras-GPT, MiniCPM, DeepSeek) plus a formal derivation and empirical evaluation of MUP to link theory and practice.

The section sets expectations for subsequent material: practical case studies, concrete recipes, and a mathematical foundation for MUP with empirical validation.

Cerebras-GPT applies Maximum Update Parametrization (MUP) to stabilize hyperparameter behavior and improve predictability of scaling curves.

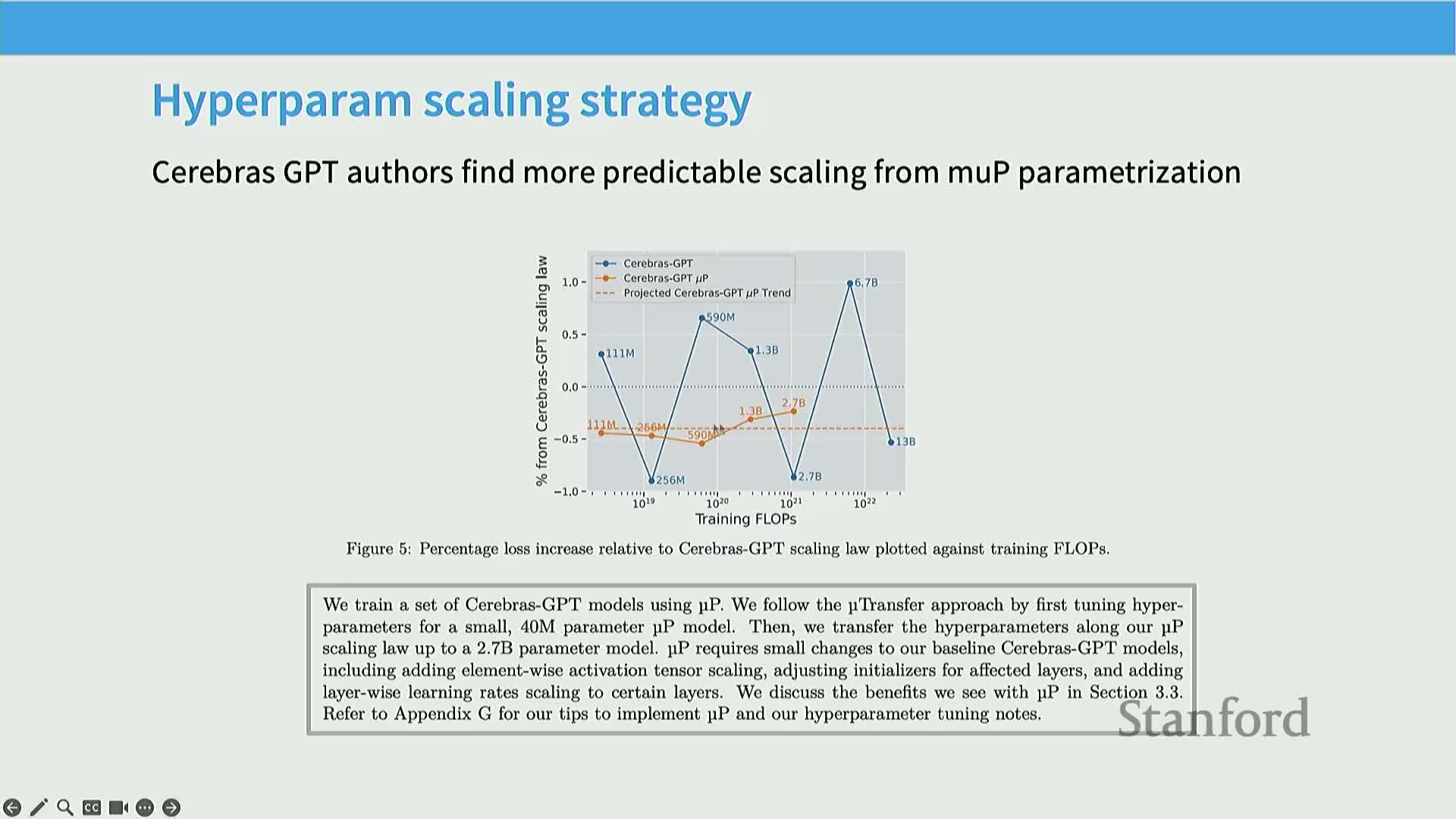
Cerebras-GPT is a family of models spanning ~0.1B to 13B parameters trained with Chinchilla-style compute/data ratios and using MUP to reduce sensitivity of optimal learning rates across scale.

Key practical points:

  • MUP initialization: nearly all non-embedding parameters scaled proportional to 1 / layer width.
  • Per-layer LR scaling: apply learning-rate multipliers inversely proportional to width, producing much smoother adherence to predicted scaling-law fits.
  • Validation strategy: perform extensive small-proxy hyperparameter sweeps (down to 40M parameter models), then scale those hyperparameters upward under MUP, showing reduced oscillation around predicted scaling points compared with standard parameterization.
  • Reproducibility artifacts: detailed appendix tables enumerate initialization differences and per-layer learning-rate multipliers between standard parameterization and MUP, enabling straightforward implementation.

MiniCPM combines MUP with a Warmup-Stable-Decay (WSD) learning-rate schedule to enable single-run Chin chilla-style data-scaling experiments and efficient proxy-model hyperparameter selection.

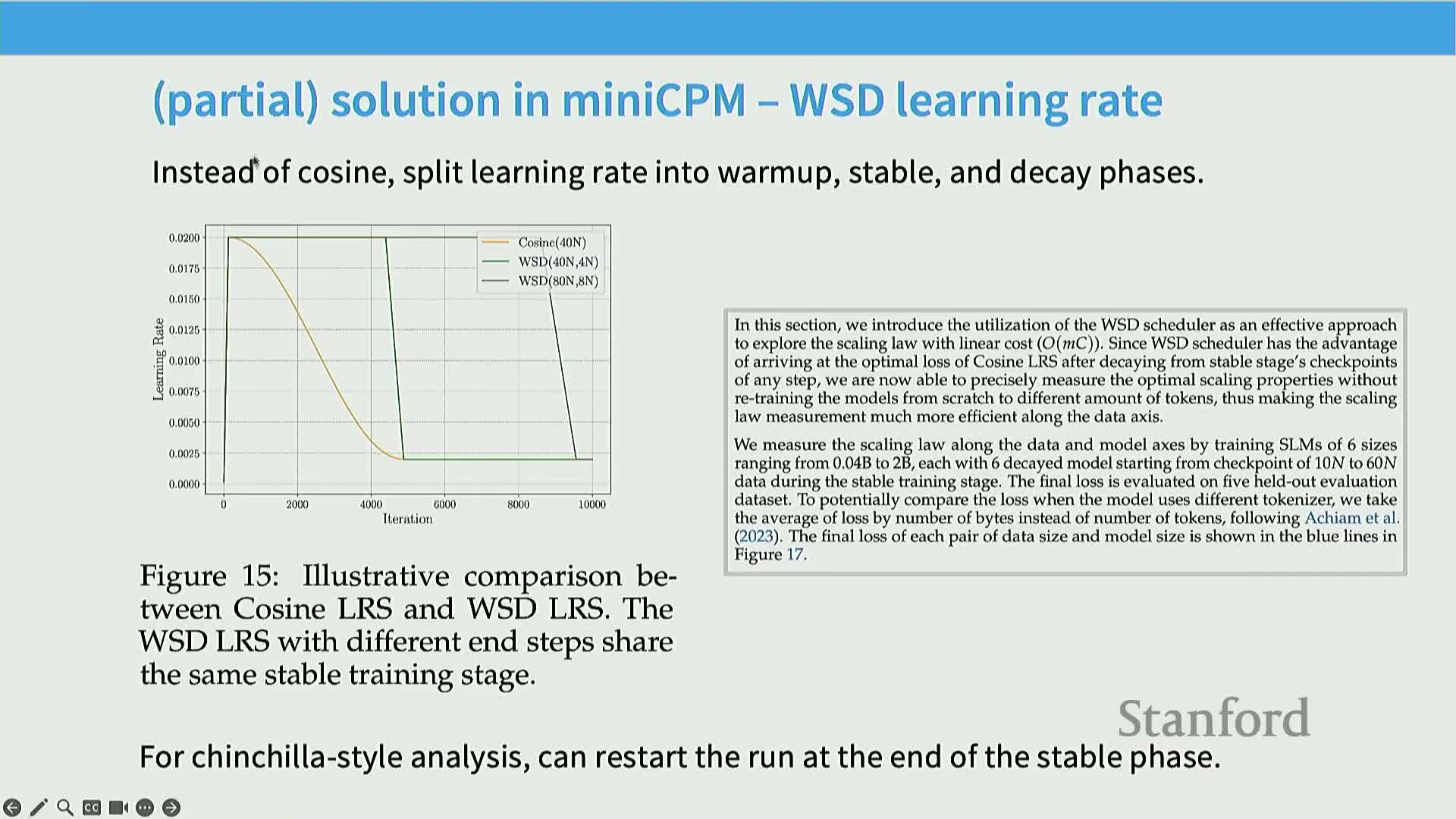
MiniCPM aims to use substantial compute to produce highly optimized small models, leveraging MUP to keep optimal hyperparameters stable when scaling width and using a WSD (Warmup–Stable–Decay) learning-rate schedule to make data-scaling reproducible from single long runs.

WSD schedule (three phases):

  1. Short warmup to ramp to the target LR.
  2. Long stable plateau at the target LR to concentrate most of the token budget.
  3. Rapid decay to a small termination LR to finish and stabilize weights.

Practical features and analyses:

  • Checkpoint rewinding and selective decay-phase application allow emulating training to different token counts without retraining from scratch.
  • Measure critical batch size scaling versus terminal loss (an isoflops-style analysis) to choose batch sizes.
  • Use two fitting methods for Chinchilla-style token-to-parameter trade-offs:
    • Take the lower envelope of training curves.
    • Jointly fit a two-variable power-law scaling law.
  • Report unusually high token-to-parameter ratios compared to original Chinchilla estimates, while cautioning that these ratios are sensitive to architecture and data quality, illustrating both the power and fragility of curve-fitting approaches.

DeepSeek performs explicit grid searches for optimal batch size and learning rate across compute scales, fits scaling laws to these optima, and extrapolates performance to large target models using WSD schedules and isoflops analysis.

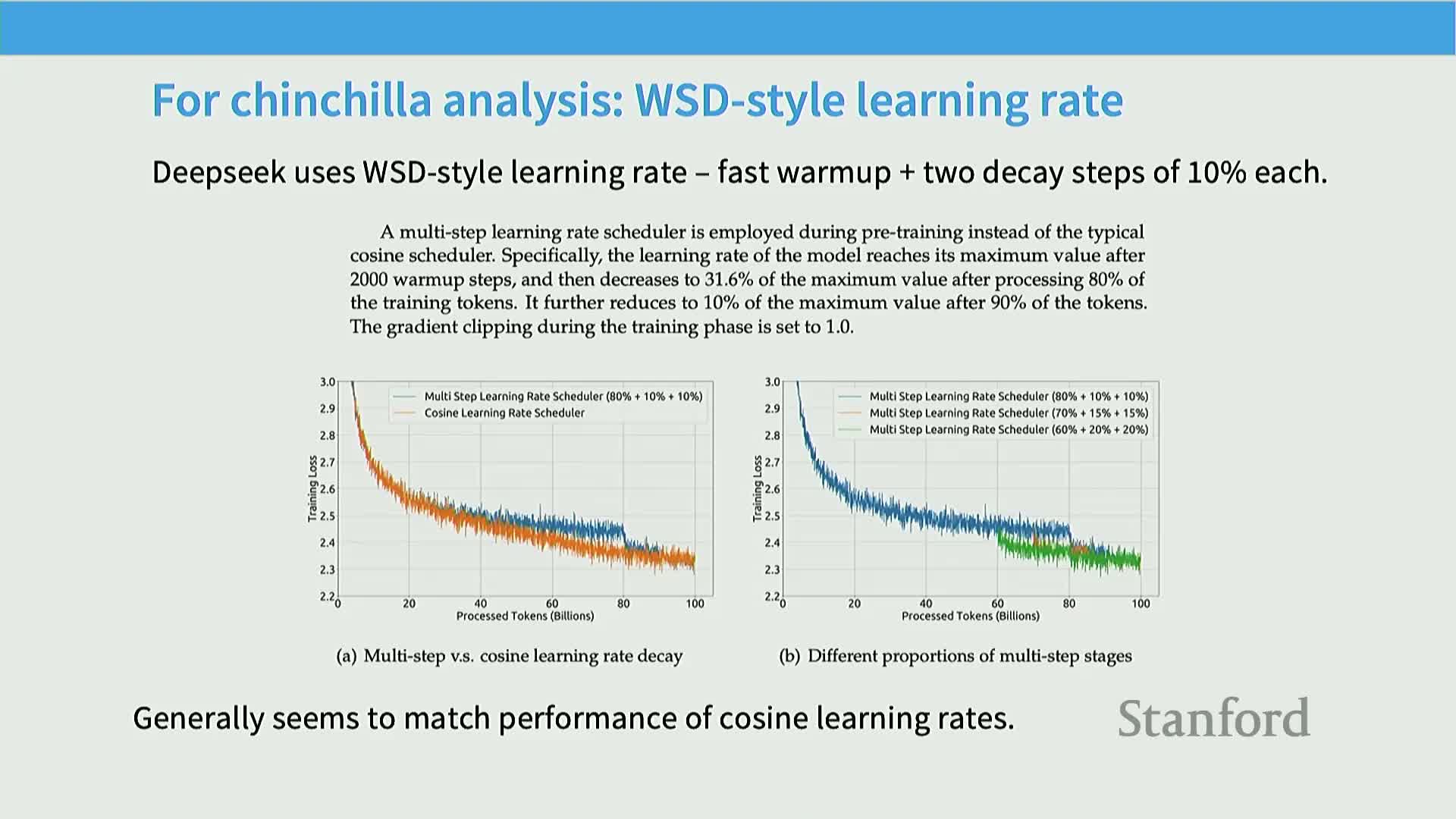
DeepSeek obtains optimal hyperparameter estimates by running grids of batch-size and learning-rate sweeps at multiple compute scales, fitting scaling relationships to the optima, and extrapolating those fits to set hyperparameters for 7B and 67B models.

Practical methodology:

  • Adopt WSD-style schedules with multiple decay phases to permit cheap Chinchilla-style experiments and concentrate compute on the effective cooldown that yields most terminal-loss improvements.
  • Replicate isoflops/Chinchilla analyses (fit quadratics to training curves, take the lower envelope) and demonstrate that extrapolated scaling laws can accurately predict held-out larger-model performance when experiments are well executed.
    Caveats:
  • Hyperparameter-scaling relations are noisier than isoflops trends, so careful experimental design and validation are required when extrapolating learning-rate and batch-size schedules.

Recent releases (Llama 3, Hunuan 1, Minimax-01) reapply isoflops/Chinchilla-style analyses and report varying optimal token-to-parameter ratios and architectural trade-offs for linear/hybrid attentions.

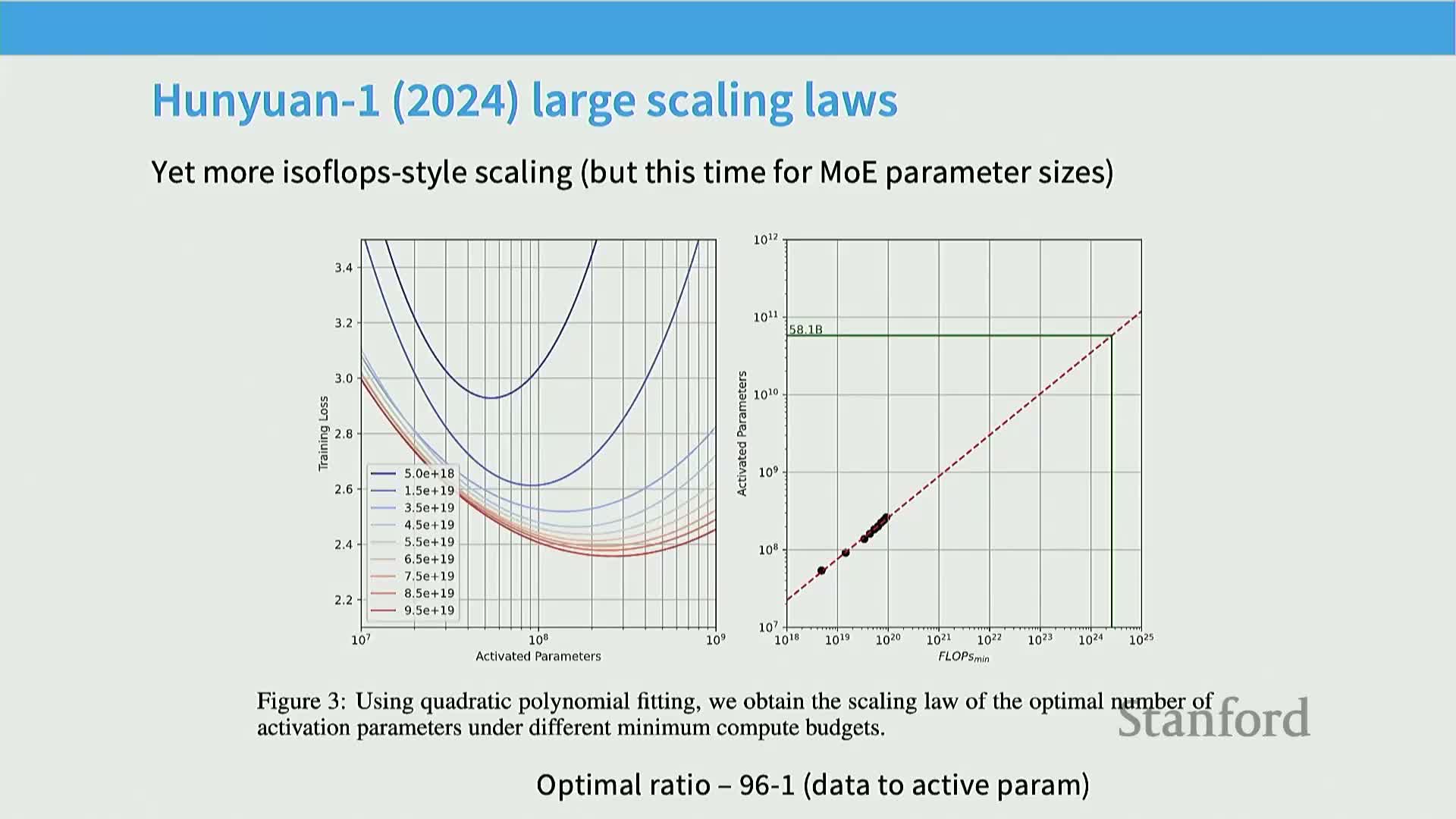
Several recent releases revisit Chinchilla-style isoflops fits and demonstrate variability in optimal token-to-parameter ratios across projects:

  • Llama 3: redoes isoflops fits and reports an optimal token-to-parameter ratio around ~39:1, higher than the original ~20:1 Chinchilla heuristic—possible causes include architecture improvements and better data quality.
  • Hunuan 1: reports even larger ratios (e.g., ~96:1) under its training regime, showing strong dependence on architecture, data, and methodology.
  • Minimax-01: investigates linear (lightning) attention and hybrid architectures and finds that under isoflops analysis, linear/hybrid attention families can achieve similar scaling performance to full softmax attention, supporting their use for long-context, linear-time models.

Across these releases, isoflops-style quadratic fits and lower-envelope methods remain reliable tools for inferring compute-to-token/model trade-offs, even though absolute ratio estimates vary by project.

Common practical scaling ingredients are stable parameterizations (e.g., MUP), WSD schedules for efficient data-scaling, isoflops/Chinchilla analyses, and fixed aspect-ratio scaling of model dimensions.

Production-grade scaling workflows typically combine several reproducible elements to reduce expensive per-scale hyperparameter searches and enable controlled extrapolation from small proxies:

  • A stable parameterization or initialization (e.g., MUP) to reduce hyperparameter drift across width or depth.
  • An LR schedule such as Warmup–Stable–Decay (WSD) to permit checkpoint-based data-scaling and reuse.
  • Isoflops/Chinchilla analyses to set token/model trade-offs and estimate critical batch sizes.
  • A fixed aspect-ratio approach when increasing total parameter counts to keep architecture proportions consistent.

These elements enable small-proxy sweeps and controlled extrapolation to target compute budgets, reducing overall experimental cost. The combination is not universal but recurs across prominent open studies and high-performance model recipes.