Course orientation and lecture goals

This session is positioned at the end of the quarter and will deep-dive into policy gradient methods for reinforcement learning (RL) applied to language models (LMs).

  • Goals:
    • Expand on prior coverage of RL with verifiable rewards rather than introduce fundamentally new theory.
    • Provide mathematical detail and code-oriented examples that connect theory to practice.
    • Focus on algorithm mechanics (e.g., policy gradients, GRPO) and on practical implementation concerns.
  • Framing:
    • Treats the lecture as a continuation and an application-focused elaboration of earlier material.

Reinforcement learning formulation for language models: states, actions, rewards, and dynamics

  • State (LM setting): the prompt concatenated with the tokens generated so far.

  • Action: generating the next token.

  • Reward characteristics:
    • Outcome-based and deterministic: rewards depend on the entire generated response (verifiable).
    • This makes signals sparse and delayed, but conceptually simpler than interactive environments.
  • Transition dynamics:
    • Trivial string concatenation: state’ = state + action.
    • This simplicity enables planning or test-time computation that physical robotics typically cannot use.
  • State representation challenges:
    • The LM synthesizes arbitrary internal tokens, so states are ungrounded text and can include internal scratchpad behavior.
    • Main challenge: ensure those token sequences produce verifiable, correct outcomes rather than merely reaching reachable but meaningless states.

Policy and objective in outcome-reward LM reinforcement learning

  • Policy: an LM conditioned on the current token sequence (prompt + generated tokens).

  • Training objective: maximize expected reward over the distribution of prompts and the policy’s token outputs.

  • Outcome-reward simplification:
    • When rewards are outcome-based, treat the entire response as a single action a with a single reward R.
    • This yields a simpler expected-reward expression and implementation.
  • Practical setup:
    • Policies often initialize from pretrained LMs and are then fine-tuned via policy optimization.
    • Rollouts produce trajectories that yield a scalar reward at episode end.
    • The objective integrates over environment-provided prompts and the stochastic policy’s responses to compute the expected return, which is the target for gradient-based optimization.

Policy gradient derivation: gradient of expected reward via log-derivative trick

  • Derivation sketch:
    • Differentiate expected reward w.r.t. policy parameters and apply the log-derivative (score function) identity to move the gradient inside the expectation.
    • Result: an expectation of **∇ log π(a s)** weighted by the return (reward).
  • Properties:
    • This gives an unbiased Monte Carlo estimator when sampling prompts and actions.
    • In the outcome-reward setting, treating the entire response as a single action further simplifies notation and implementation.
    • This score-function estimator is the basis for sampling-based updates that seek to increase expected reward.

Naive policy gradient as reward-weighted supervised fine-tuning and implications of binary rewards

  • Naive policy gradient update:
    • Sample prompts and model responses, then apply gradient steps proportional to the sampled reward.
    • Analogy: similar to supervised fine-tuning (SFT), but responses are weighted by reward rather than matched to fixed human targets.
  • Special cases and failure modes:
    • With binary rewards (0/1), updates occur only for rewarded responses: effectively SFT on the subset of model outputs deemed correct.
    • In sparse-reward regimes, if the policy rarely produces positive responses, gradients are near zero and learning can stall.
    • Conclusion: naive sampling without variance reduction or reward shaping can leave the model stuck when initial performance is poor.

Dataset non-stationarity and contrast with continuous reward RLHF

  • Non-stationarity:
    • Policy optimization changes the policy that generates training examples, so the empirical dataset evolves across iterations.
    • This can be beneficial if the policy discovers easy positives and generalizes to harder prompts, but it complicates analysis and monitoring because the data distribution shifts.
  • Reward-model contrast:
    • RL with human feedback typically uses a learned, continuous reward model, which provides graded values and reduces sparsity relative to binary verifiable rewards.
    • The choice between verifiable outcome rewards and learned reward models affects algorithm design, hyperparameter choices, and intuitions about training dynamics.

Baselines for variance reduction in policy gradient

  • Baseline b(s):
    • Any function of state (but not of action) that is subtracted from returns in the policy gradient estimator to reduce variance without biasing the gradient.
  • Why it’s unbiased:
    • Subtracting b(s) leaves the expected gradient unchanged because the baseline term factors out of the expectation over actions for a given state and contributes zero in expectation.
  • Practical notes:
    • Baselines are fundamental to stabilize and accelerate convergence by centering the reward signal.
    • Valid baselines include fixed constants or learned value estimators, provided they do not depend on the action.
    • The design of b(s) substantially affects gradient variance and empirical learning speed.

Toy two-state example illustrating variance pitfalls and baseline benefits

  • Two-state toy example (intended insight):
    • Two prompts (states) with different per-action rewards show how naive updates can favor misleadingly high absolute rewards in certain states and produce suboptimal policies.
    • If the policy randomly selects an action that yields high reward in an easy state, repeated updates can amplify that action and eliminate the true global optimum—an instance of high-variance, myopic updates.
  • Remedy:
    • Introduce a state-dependent baseline (e.g., subtract per-state expected reward) to center rewards, dramatically reducing variance and preventing harmful relative gradients.
    • The example quantifies how appropriate baselines can shrink variance by multiple factors and improve convergence behavior.

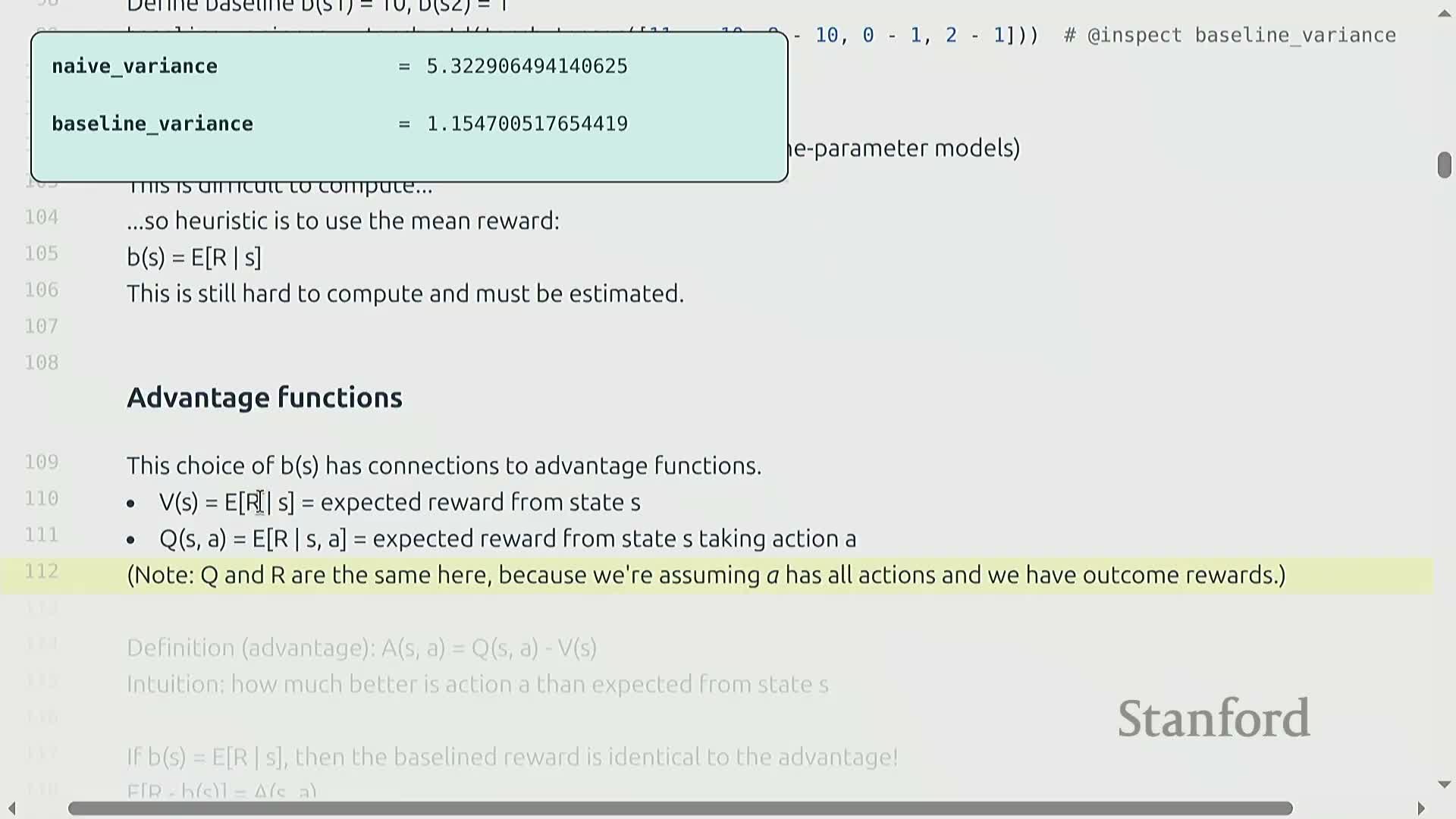
Optimal baseline expression and practical heuristic choice

  • Optimal baseline properties:
    • For scalar-parameter models, the variance-optimal baseline has a closed-form involving expectations of squared score-function terms weighted by returns.
    • In higher dimensions, the optimal solution requires covariance matrices and becomes impractical to compute exactly.
  • Practical heuristic:
    • Use the estimated expected reward given state (value estimate) as the baseline—this approximates the advantage function and typically yields substantial variance reduction.
    • Value estimates are tractable to obtain via sampling or simple learned value functions, so implementations favor these computable approximations balancing cost and variance reduction.

Advantage function and unified delta notation for algorithms

  • Advantage function A(s,a):
    • Defined as Q(s,a) − V(s): how much better action a is relative to average behavior at state s.
    • Provides a principled baseline choice when available.
  • Outcome-reward simplification:
    • In the outcome-reward LM setting, Q and the return R coincide when treating the entire response as the return, so A = return − expected return given state.
  • Implementation abstraction:
    • Many algorithms adopt a unified scalar delta to represent whatever multiplier (reward, centered reward, normalized advantage, etc.) is used with the log-probability gradient.
    • Variants differ primarily in how delta is computed, clarifying that modern policy-gradient techniques scale the score-function gradient by a carefully chosen delta to control variance and bias.

GRPO lineage and group-structured variance reduction in LM settings

  • Lineage and structure exploitation:
    • GRPO and related algorithms evolved from the PPO/DPO lineage but exploit structure specific to language modeling.
    • Key LM structure: you can sample multiple responses per prompt, forming natural groups for per-prompt baselines (group means).
  • Benefits of grouped sampling:
    • Compute an empirical baseline across responses from the same prompt, which reduces variance without requiring a global learned value function.
    • When rollouts are naturally grouped (many responses per prompt), GRPO-style relative updates are practical and effective.
    • In environments without grouping, alternative value-estimation methods are required.
  • Algorithmic consequences:
    • Group structure motivates clipping and normalization strategies that compare responses relative to their prompt-specific cohort.

Toy sorting task and reward design alternatives

  • Toy environment: sorting n numbers.
    • Prompt: a sequence of numbers.
    • Desired response: the sorted sequence.
    • Reward must quantify closeness to ground truth.
  • Possible reward formulations:
    • Binary correct/incorrect: severe sparsity.
    • Position-match counts: partial credit by summing positions that match the sorted result.
    • Inclusion-plus-adjacency: points for presence of prompt tokens and for correctly sorted adjacent pairs—richer shaping signals.
  • Reward-engineering trade-offs:
    • Too sparse: prevents learning.
    • Too permissive: can be exploited or mislead optimization.
    • Designing a reward that balances informativeness and robustness is a critical practical decision.

Simplified model architecture and sampling strategy for the sorting task

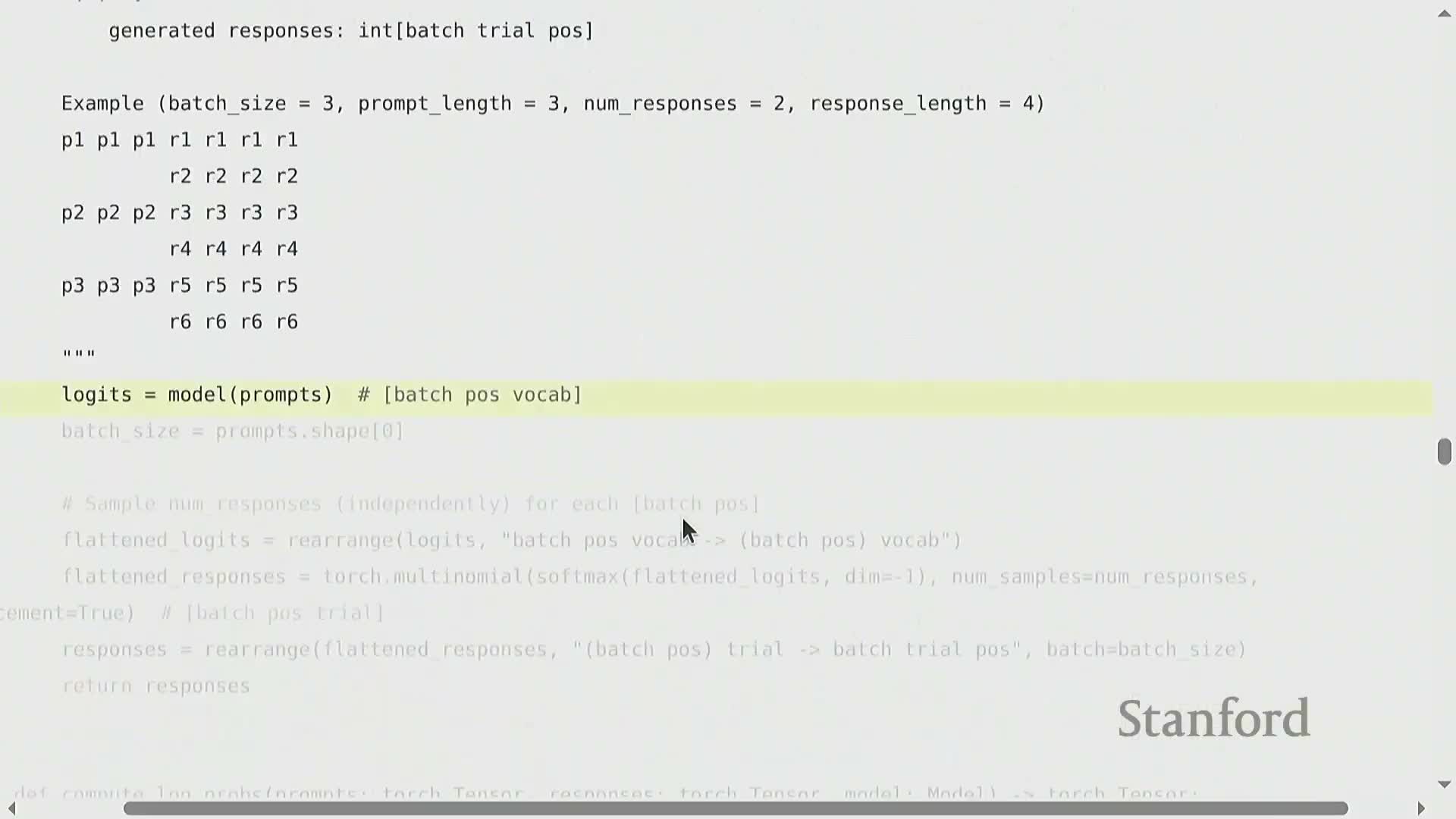
  • Minimal parametric model for on-laptop experiments:
    • Fixed, equal prompt and response lengths to simplify indexing.
    • Positional information captured via per-position parameter matrices.
    • Encoding collapses position embeddings into a prompt summary.
    • Decoding produces logits per response position independently (non-autoregressive) to simplify implementation.
  • Forward pass:
    • Map batch-by-position inputs through embeddings and per-position linear transforms to produce logits over the vocabulary for each output position.
    • Use logits to sample multiple response trials per prompt.
  • Rationale:
    • Trades realism for tractability but preserves core elements needed to illustrate policy-gradient training, grouped sampling, and reward-driven updates.

Computing deltas: centering, normalization, and optional max-only selection

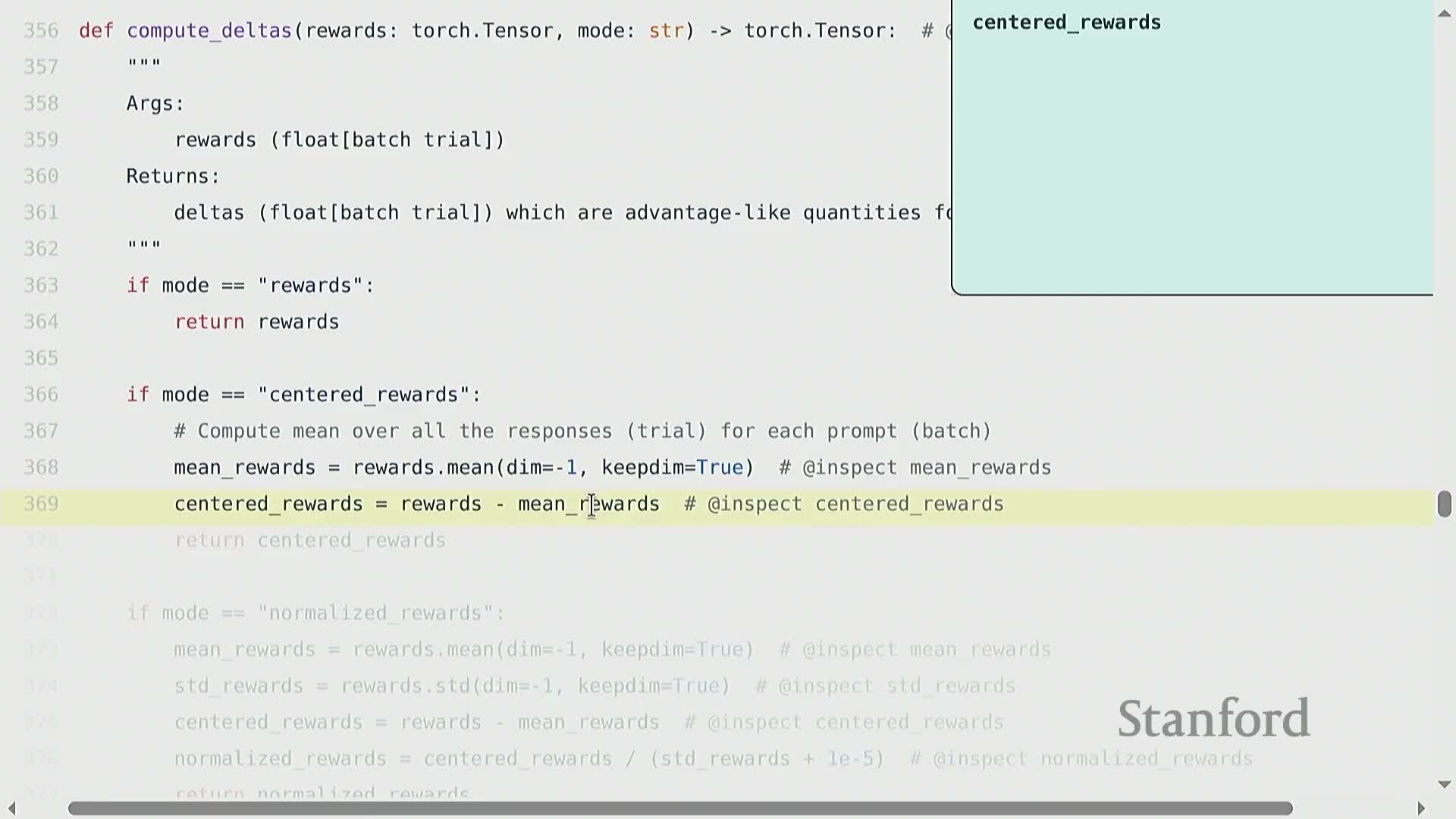
  • compute_deltas: converts raw rewards into scalar multipliers for gradient updates. Common choices include:
    • Raw rewards (no transformation).
    • Centering by subtracting per-prompt means.
    • Normalization by dividing by standard deviation (with epsilon for numerical stability).
    • Max-only: zero out any response that is not the batch maximum.
  • Practical effects:
    • Centering turns sparse 0/1 rewards into both positive and negative signals, so incorrect responses produce negative updates and correct ones positive—helps learning when positives are rare.
    • Normalization yields scale invariance to multiplicative reward changes.
    • Max-only selection enforces an all-or-nothing strategy to avoid rewarding trivial partial-credit solutions.
  • Takeaway:
    • The chosen delta transformation profoundly affects update direction, stability, and sensitivity to reward scaling.

Log-probability extraction and naive policy-gradient loss computation

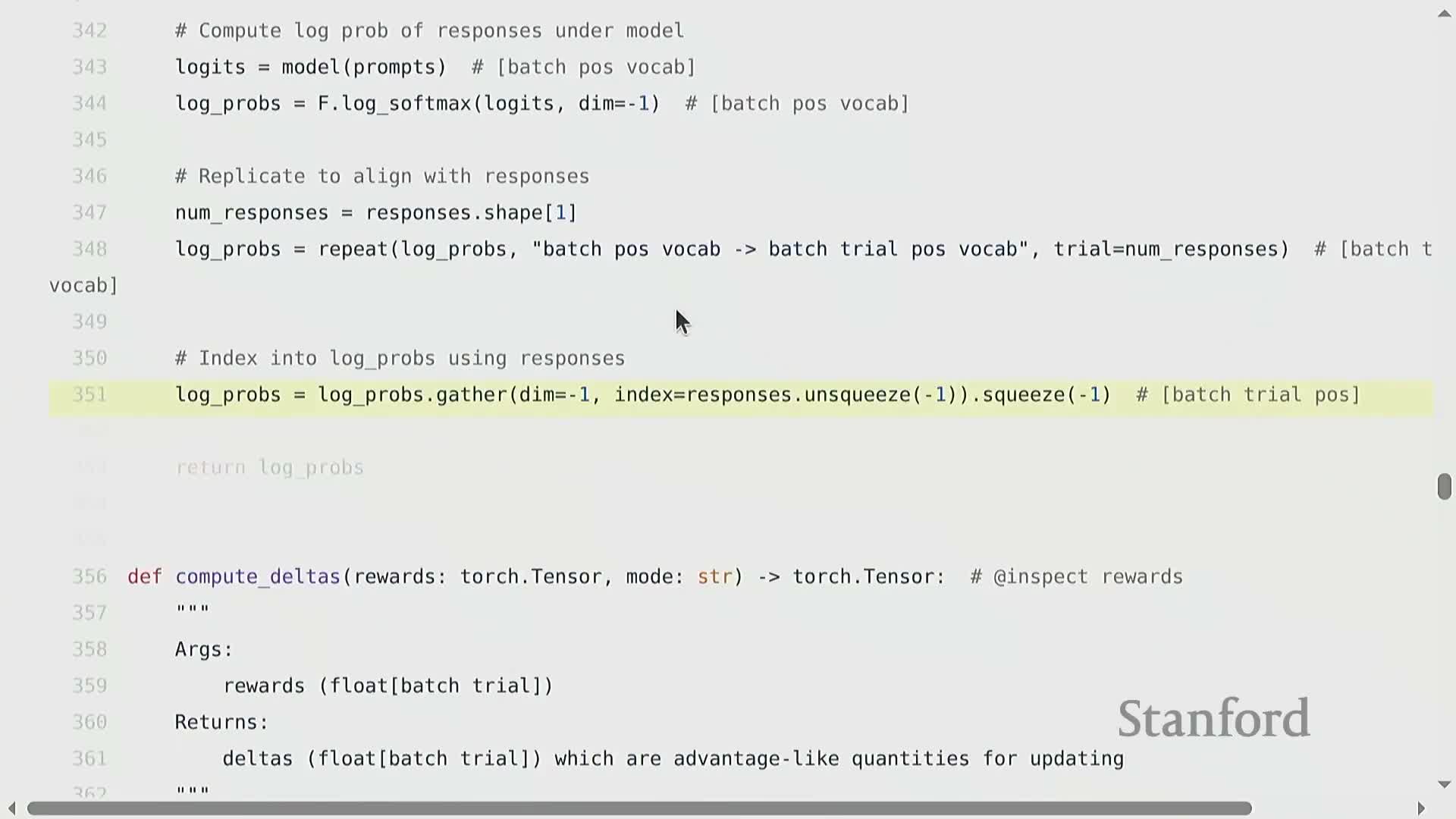
  • Computing log-probabilities and loss:
    • After sampling and scoring responses, compute the log-probability of each sampled token sequence by indexing model logits at the chosen token indices and summing or averaging across positions.
  • Naive policy-gradient loss (outcome reward regime):
    • Broadcast the per-response delta to all positions for that response.
    • Multiply the delta by the corresponding per-position log-probabilities and form the (negative) expected delta-weighted log-probability averaged across batch and trials.
  • Notes:
    • This direct score-function estimator implements the Monte Carlo policy gradient for both non-autoregressive and autoregressive decodings.
    • Position broadcasting reflects the single-return-per-response assumption.
    • The loss is modular: different delta computations (centered, normalized, clipped) can plug into the same gradient pipeline.

Freezing reference quantities (no-grad) and importance-ratio pitfalls

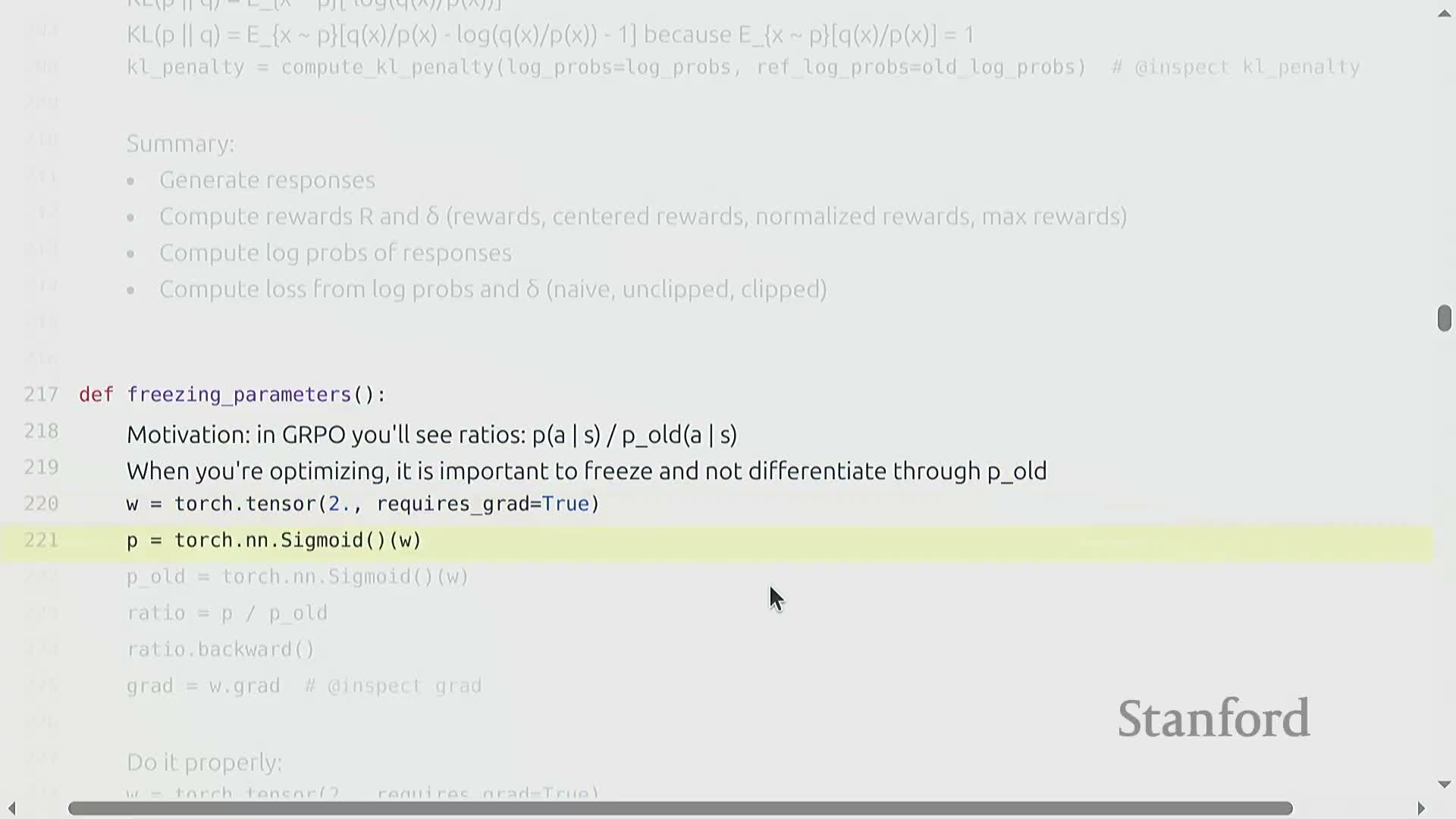
  • Importance-weighted ratios (pi_theta / pi_old):
    • Treat the denominator as a constant by disabling gradient flow through the old-policy computation.
    • If you differentiate through both numerator and denominator, you can nullify gradients (e.g., ratio of identical parameterizations yields 1 and zero gradient), defeating learning.
  • Implementation guidance:
    • Wrap old-policy log-probabilities or probabilities in no-grad contexts or cache scalar log-probabilities from a frozen checkpoint so the backward pass only propagates through the current policy.
    • This engineering detail is critical for correctness when using PPO-style clipping or importance-weighted gradient estimators.

Credit assignment and discounting considerations for outcome rewards

  • Credit assignment challenges:
    • Classical RL tools like discounting and bootstrapping are ambiguous when the reward is only available at episode end and many intermediate token decisions can matter.
    • Discounting earlier tokens is not obviously beneficial because early strategic choices may determine later correctness more than later tokens themselves.
  • Practical approaches:
    • Often smear credit across the entire response (broadcast final reward to all token positions).
    • Or design process-level rewards if reliable intermediate signals exist.
  • Ongoing challenge:
    • Designing effective credit-assignment mechanisms remains a core difficulty in sparse-reward LM tasks.

GRPO clipped objective and KL regularization

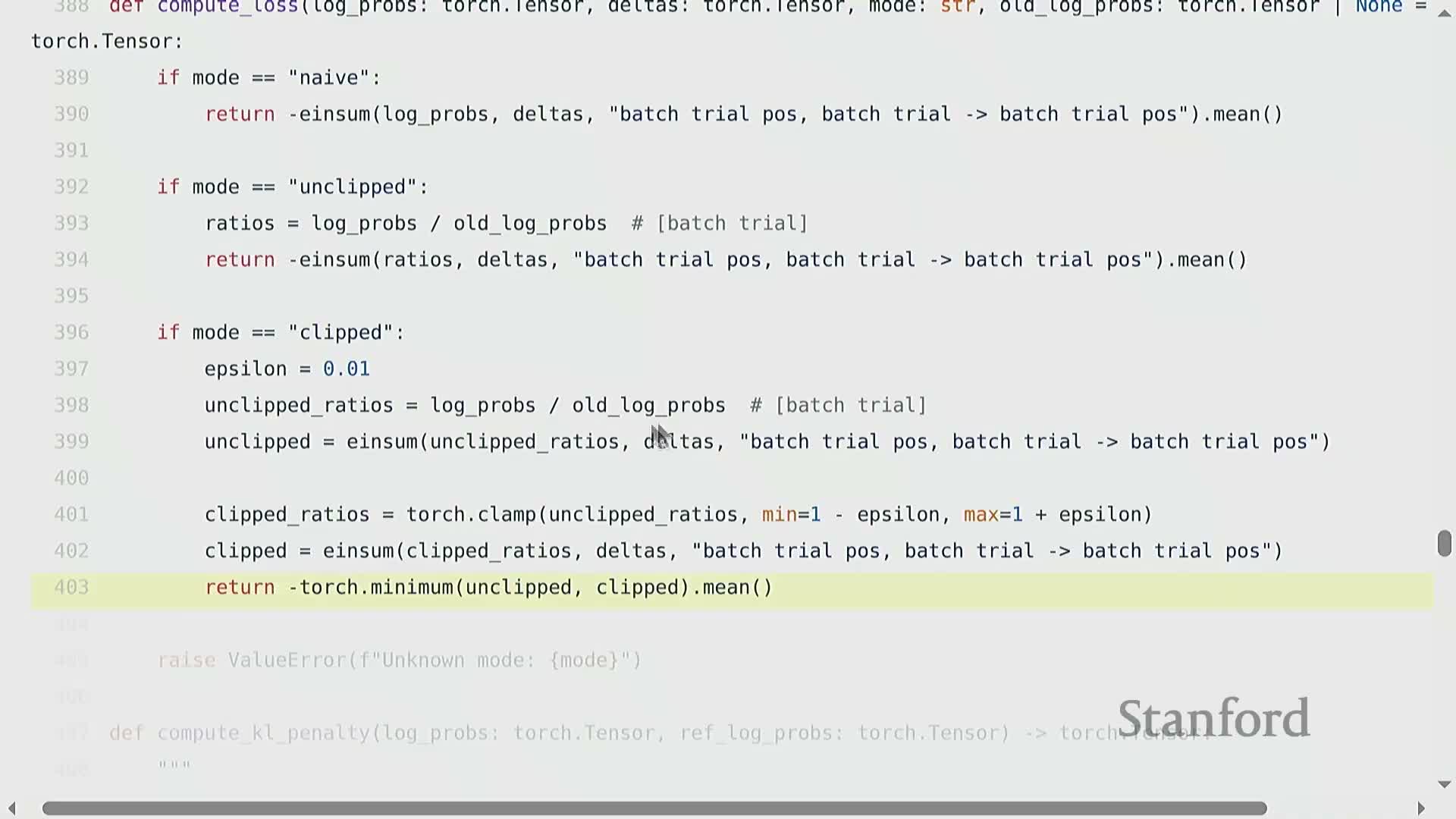
  • GRPO loss (group-relative, PPO-style):
    1. Compute importance-weighted ratios between current and old policies for sampled responses.
    2. Multiply ratios by deltas (reward/advantage variants).
    3. Clip ratios to [1 − ε, 1 + ε] to bound update magnitudes and prevent destructive policy shifts.
    4. Take the minimum of the unclipped and clipped ratio-weighted deltas (with sign change to convert reward maximization into loss minimization).
  • Regularization:
    • An auxiliary KL penalty between the current policy and a slowly updated reference policy provides additional stabilization.
    • Unbiased but lower-variance estimators of KL are possible via algebraic rearrangement (e.g., q/p − log(q/p) − 1 forms).
  • Purpose:
    • Clipping and KL regularization are practical mechanisms to stabilize policy updates in LM fine-tuning contexts.

Algorithm components, inner/outer loop structure, and computational workflow

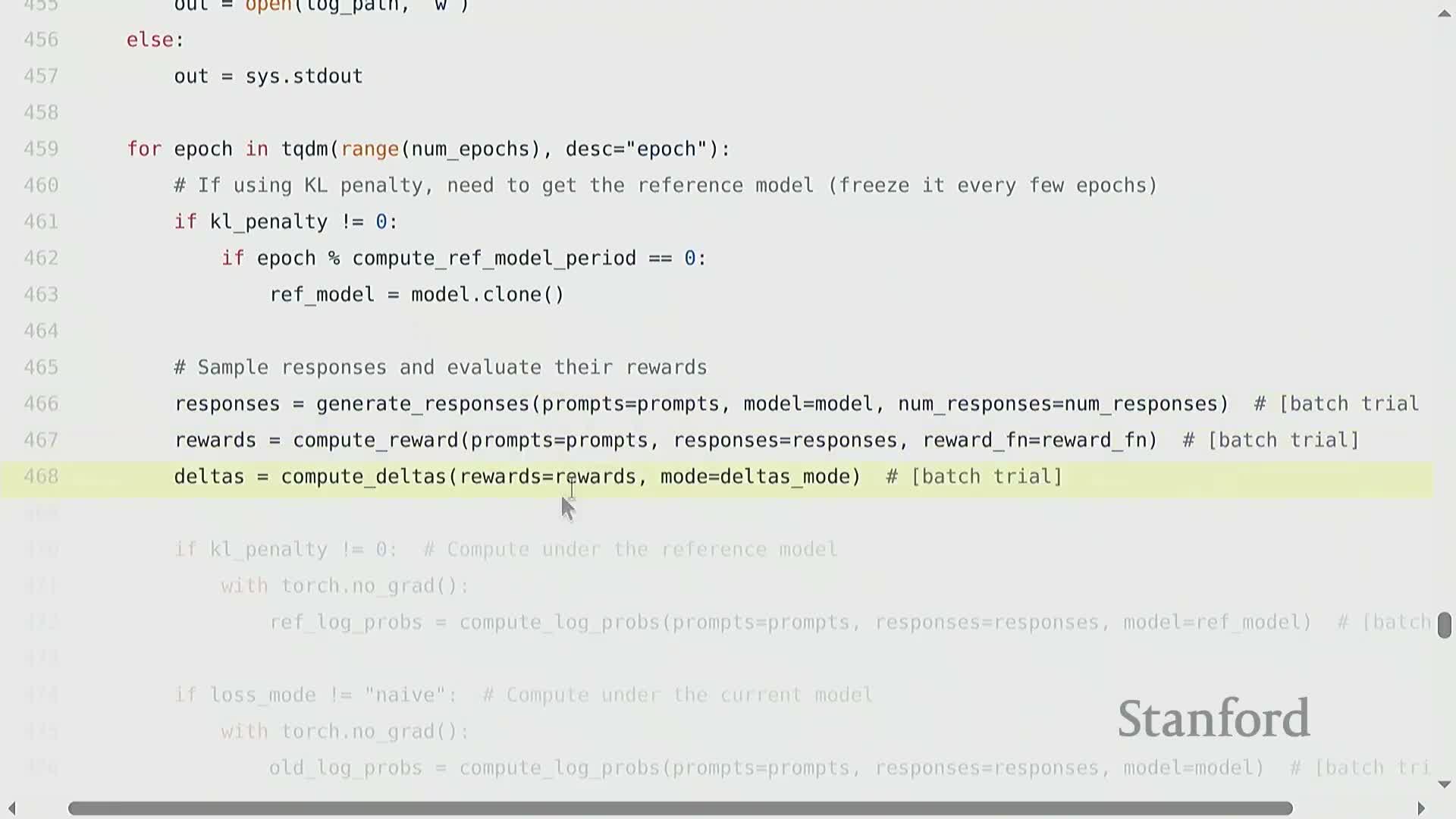
  • Typical training loop structure:
    1. Outer loop: generate a fresh batch of responses (inference rollouts).
    2. Inner loop: perform multiple gradient steps on that static set of rollouts to amortize expensive sampling costs.
  • Key components:
    • Current policy being trained.
    • Frozen old policy used to compute importance ratios for clipping.
    • Slower-moving reference policy for KL regularization (updated less frequently).
  • Practical considerations:
    • Cache log-probabilities from the rollout stage to avoid recomputing frozen-model outputs and reduce compute/memory needs.
    • Architecting inference workers, checkpointing, and distributed pipelines is a major engineering concern beyond the scalar algorithmic choices.
    • The inner/outer loop design reflects a trade-off between sample efficiency and inference cost at scale.

Why a separate KL reference vs. old policy and initialization considerations

  • Role of a slowly updated reference model for KL regularization:
    • Decouples the long-term regularization target from the short-term importance-ratio stabilization provided by the old policy.
    • Helps define a stable optimization objective over inner-loop updates.
  • Practical notes:
    • If the KL target were the immediately previous policy (changing on the same timescale), regularization would shift too rapidly and could undermine convergence.
    • Common practices: use a frozen checkpoint or periodic parameter copies as a constant regularization anchor; compute pi_old quantities from cached log-probabilities.
    • Even when pi_old equals the current policy in initial iterations, valid updates occur because pi_old is treated as a constant in gradient computations.

Empirical sorting-task experiments and learning curve interpretation

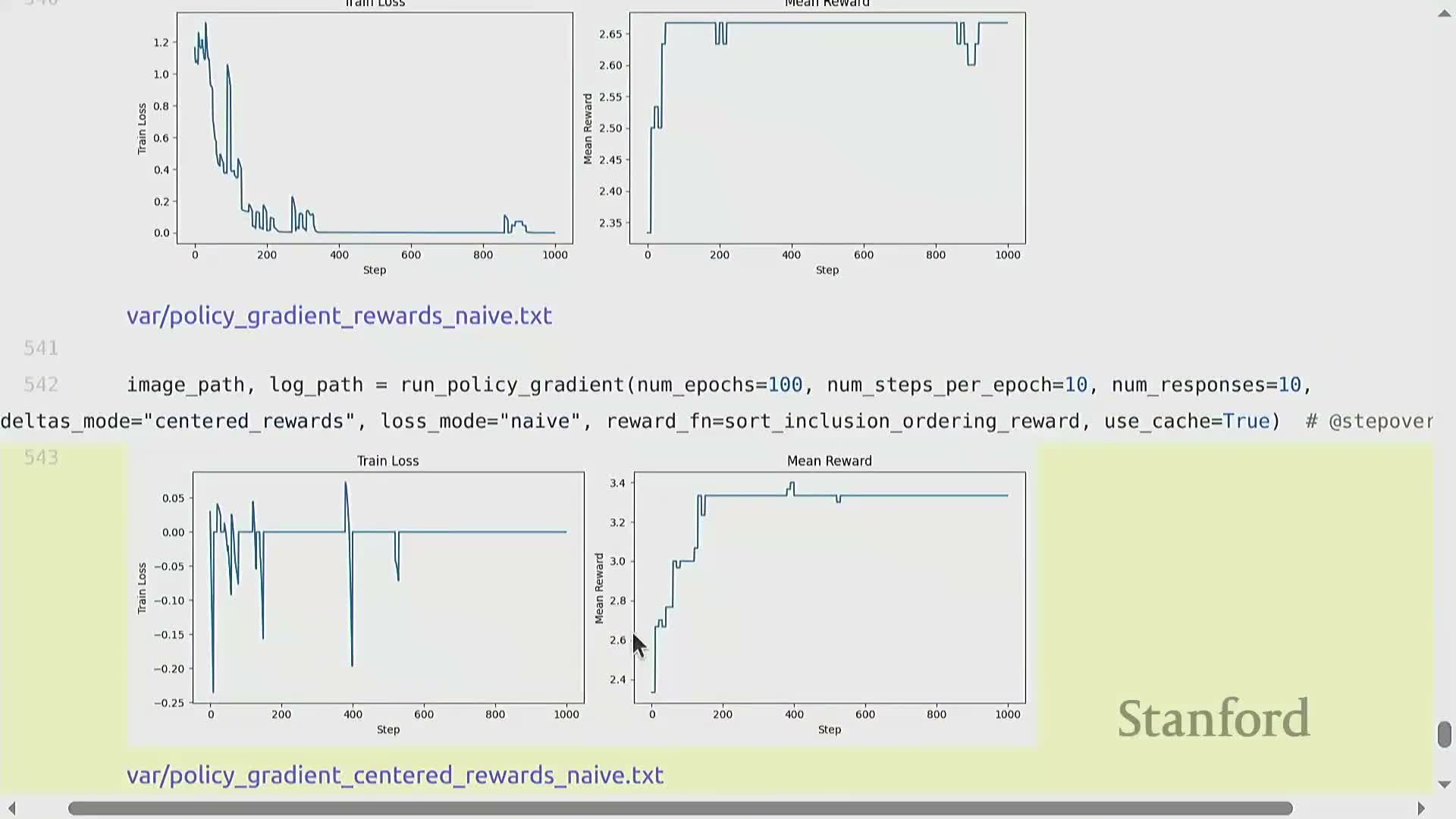
  • Empirical observations on the toy sorting task:
    • Centered-reward updates often yield modest mean-reward improvements, pushing the policy away from lower-reward responses within a prompt cohort.
    • Limitations:
      • If all sampled responses for a prompt have identical rewards, centered deltas become zero and produce no update for that batch.
      • Loss curves can be misleading because the data distribution changes as the policy evolves.
  • Monitoring recommendations:
    • Track reward metrics on held-out prompts or regenerate rollouts to assess true progress.
    • Experiments illustrate sensitivity to reward design, delta transformations, sampling variance, and the need for careful hyperparameter tuning.

Conclusions: promise of RL for LMs and scaling challenges

  • Why use RL for LMs:
    • Optimizes behaviors that exceed imitation-limited supervised data by directly optimizing measurable objectives when verifiable rewards exist.
    • Powerful for improving LM performance on tasks with quantifiable outcomes.
  • Persistent challenges:
    • Sparse and delayed rewards.
    • High variance in Monte Carlo estimators.
    • Reward-design vulnerabilities (hackability/exploitation).
    • Complex credit assignment across long token sequences.
  • Systems-level complexity:
    • Building scalable RL for LMs adds engineering burden beyond pretraining: inference cost, multi-model orchestration (policy, old policy, reference, reward models), and distributed execution must be managed.
  • Outlook:
    • Continued research on reward specification, variance reduction, and system-level infrastructure is necessary to realize RL’s potential for large-scale language-model improvement.