Foundations of Machine Learning
(Work in progress I will gradually add more content when having more time:D Please stay tuned :D)
Machine Learning Paradigms
Supervised learning
Supervised learning is a type of machine learning where the model is trained on a labeled dataset, meaning that the input data is paired with the correct output. The model learns to make predictions based on this labeled data.
Mathematically, given a training set of \(N\) samples:
\[\mathcal{D} = \{(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)\}\]where \(x_i \in \mathbb{R}^d\) is the input feature vector with \(d\) dimensions. The corresponding label \(y_i\) can be either a continuous value \(y_i \in \mathbb{R}\) for regression problems, or a categorical value \(y_i \in \{0, 1, \ldots, K-1\}\) for classification problems.
the goal of supervised learning is to learn a function \(f_{\theta}\) parameterized by \(\theta\) that maps input features \(x\) to output labels \(y\), i.e., \(\hat{y} \triangleq f_{\theta}(x) \approx y\).
It can be done by minimizing the loss function - which measures the discrepancy between the predicted output \(\hat{y}\) and the true output \(y\) over the training set, i.e., \(\mathcal{L}(\theta) = \frac{1}{N} \sum_{i=1}^{N} \mathcal{l}(y_i, f_{\theta}(x_i))\).
Common loss functions:
- Mean squared error (MSE) for regression problems:
- Cross-entropy loss for classification problems:
where \(y_{ik}\) is the one-hot encoded label for the \(i\)-th sample and the \(k\)-th class, and \(\hat{y}_{ik}\) is the predicted probability of the \(i\)-th sample for the \(k\)-th class.
More advanced topics which are discussed later in this post:
- Advanced loss functions
- Regularization
- Bias-variance tradeoff
- Out-of-distribution generalization
- Adversarial generalization/training
- Sharpness-aware minimization
Unsupervised learning
Unsupervised learning is a machine learning paradigm where a model learns patterns, structures, or representations from unlabeled data without explicit supervision.
Unlike supervised learning, there is no unified mathematical formulation for unsupervised learning, instead, it is a collection of different techniques/problems that can be grouped into following categories:
Dimensionality reduction/representation learning: Finding a low-dimensional representation of the data that captures the most important information, e.g., to learn a mapping \(f: \mathbb{R}^d \rightarrow \mathbb{R}^k\) where \(k \ll d\). Common methods include Principal Component Analysis (PCA), t-SNE, and Autoencoders.
Clustering: Finding groups of similar features, e.g., assigning cluster \(c_i\) to each sample \(x_i\), where \(c_i \in \{1, 2, \ldots, K\}\). Common methods include K-means, Gaussian Mixture Models (GMM), and Hierarchical Clustering.
Density estimation: Estimating the probability distribution \(p(x)\) of the data. Common methods include Parametric models (e.g., Gaussian Mixture Models (GMM), Mixture of Experts (MoE)), Non-parametric models (e.g., Kernel Density Estimation (KDE), Histogram), and Variational Autoencoders (VAEs).
Parametric methods are the ones that assume the data follows a known distribution (e.g., Gaussian, MoG, etc.) and characterize by a fixed number of parameters that do not grow with the amount of data.
Non-parametric methods are the ones that do not make any assumptions about the distribution of the data. The number of parameters can grow with more data. It provides greater flexibility but requires more data/computational expense.
Gaussian Mixture Model (GMM) models the data as a weighted sum of \(K\) Gaussian distributions:
\[p(x) = \sum_{k=1}^{K} \alpha_k \mathcal{N}(x; \mu_k, \Sigma_k)\]where \(\alpha_k\) is the mixing coefficient, \(\mu_k\) is the mean, and \(\Sigma_k\) is the covariance matrix of the \(k\)-th Gaussian distribution. It can be learned using Expectation-Maximization (EM) algorithm, including the E-step and M-step:
E-step: compute the probability that each sample \(x_i\) belongs to each cluster \(k\):
\[p(c_i = k \mid x_i) = \frac{\alpha_k \mathcal{N}(x_i; \mu_k, \Sigma_k)}{\sum_{j=1}^{K} \alpha_j \mathcal{N}(x_i; \mu_j, \Sigma_j)}\]M-step: update the parameters of the Gaussian distributions to maximize the likelihood of the data:
\[\alpha_k = \frac{1}{N} \sum_{i=1}^{N} p(c_i = k \mid x_i)\] \[\mu_k = \frac{\sum_{i=1}^{N} p(c_i = k \mid x_i) x_i}{\sum_{i=1}^{N} p(c_i = k \mid x_i)}\] \[\Sigma_k = \frac{\sum_{i=1}^{N} p(c_i = k \mid x_i) (x_i - \mu_k)(x_i - \mu_k)^T}{\sum_{i=1}^{N} p(c_i = k \mid x_i)}\]And repeat the E-step and M-step until convergence.
Kernel Density Estimation (KDE) uses a kernel function to estimate the probability density function of the data.
\[p(x) = \frac{1}{Nh} \sum_{i=1}^{N} K \left( \frac{x - x_i}{h} \right)\]where \(K\) is the kernel function and \(h\) is the bandwidth to control the smoothness of the estimated density. Common kernel functions include Gaussian, Epanechnikov, and Uniform kernels.
Self-supervised learning
Clustering
Semi-supervised learning
Reinforcement learning
Machine Learning Settings
Representation learning
Continual learning
Meta-learning
Transfer learning
Multi-task learning
Domain adaptation
Unsupervised domain adaptation
Given a set of \(N \leq 1\) source domains \(\{ \mathcal{D}_{S_i} \}_{i=1}^{N}\) each of which is a collection of data-label pairs of domain \(S_i\), i.e., \(\mathcal{D}_{S_i} = \{ (x_{j}, y_{j}) \}_{j=1}^{N_{S_i}}\), \(y_i \in [K] := \{1, 2, \ldots, K\}\), (the set of classes \(K\) is the same for all domains), and one unlabeled target domain \(\mathcal{D}_T=\{x_j\}_{j=1}^{N_T}\), the goal of unsupervised domain adaptation is to learn a classifier \(f_{\theta}\) that can generalize well to the target domain \(\mathcal{D}_T\).
Example:
- Source domain: Images of faces from different countries, each country can be considered as a domain with different geographic features.
- Target domain: Images of faces from a specific country that does not have the same geographic features as the source domains and no labels. It can be a rare race or ethnicity.
Supervised domain adaptation
The setting is similar to unsupervised domain adaptation, but the target domain has labels.
Challenges
Domain generalization
Optimization
Gradient descent
Newton’s method
Fisher information
Hessian matrix
Stochastic gradient descent
Adam, RMSProp, AdaGrad
Bayesian Optimization
Bias-Variance
Bias – Error due to overly simplistic assumptions in the model.
- High bias models underfit the data because they fail to capture important patterns.
- Example: A linear regression model trying to fit a complex, nonlinear dataset.
Variance – Error due to excessive sensitivity to training data.
- High variance models overfit the data by learning noise along with patterns.
- Example: A deep neural network memorizing training data instead of generalizing.
It is a worth noting that bias or variance is measured on the validation set, not the training set.
\[\text{Bias} = \mathbb{E}[\hat{f}(x)] - f(x)\]- high bias means large errors due to incorrect assumptions or model is too simple
- low bias means small errors, and close to the ground truth
- high variance means the model makes different predictions each time after training on different datasets.
- low variance means similar predictions on different datasets
Tradeoff
- A model with high bias and low variance is simple but inaccurate (underfitting).
- A model with low bias and high variance is flexible but unreliable (overfitting).
- The goal is to find a balance—an optimal point where bias and variance are minimized to achieve good generalization.
How to Control Bias-Variance Tradeoff?
- Increase model complexity to reduce bias (e.g., moving from linear to polynomial models).
- Reduce complexity to lower variance (e.g., regularization, pruning in decision trees).
- Use more training data to help models generalize better.
- Use ensemble methods like bagging and boosting to balance bias and variance.
Bagging and Boosting
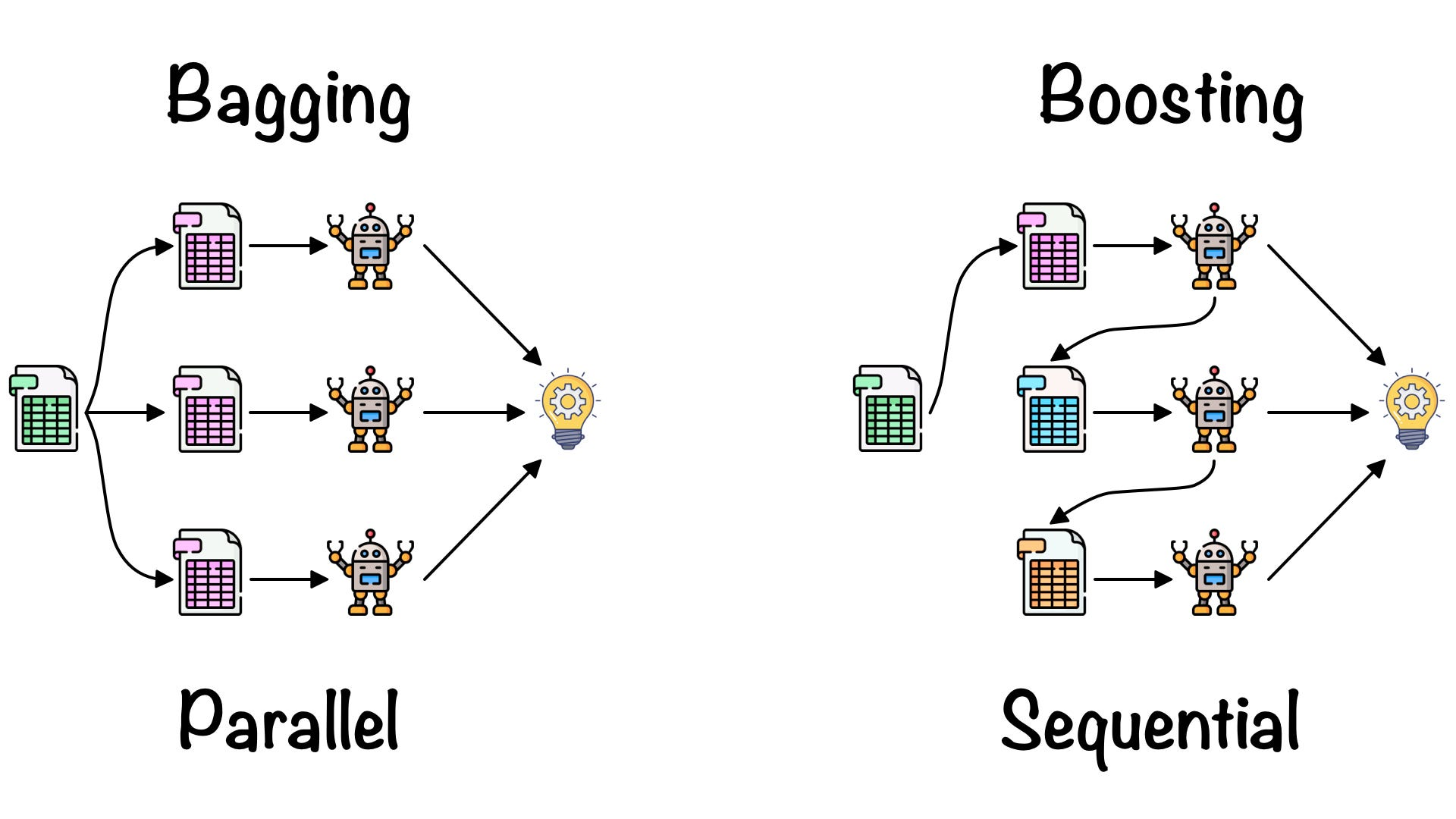
Reference: https://towardsdatascience.com/ensemble-learning-bagging-boosting-3098079e5422
Bagging (Bootstrap Aggregating)
💡 Goal: Reduce variance and prevent overfitting by training multiple models in parallel and averaging their predictions.
How it works?
- Bootstrap Sampling: Random subsets of training data (with replacement) are drawn.
- Train Weak Learners: Independent models (often decision trees) are trained on these subsets.
- Aggregate Predictions:
- For regression: Take the average of predictions.
- For classification: Use majority voting.
Boosting
💡 Goal: Reduce bias and improve weak models by training them sequentially, where each new model focuses on the errors of the previous one.
How it works?
- Train a Weak Model (e.g., a shallow decision tree).
- Identify Errors: Assign higher weights to misclassified instances.
- Train the Next Model: Focus more on difficult cases.
- Repeat: Continue training models sequentially, combining them for the final prediction.
Popular Boosting Algorithms
🔥 AdaBoost (Adaptive Boosting)
- Adjusts sample weights to focus on hard-to-classify instances.
- Final prediction is a weighted sum of weak models.
🔥 Gradient Boosting (e.g., XGBoost, LightGBM, CatBoost)
- Models are trained sequentially to minimize the residual errors of previous models.
- Uses gradient descent to optimize performance.
🔥 Boosted Trees (e.g., XGBoost)
- A more efficient version of gradient boosting that includes regularization.
- Popular for Kaggle competitions and real-world ML tasks.
XGBoost
K-Nearest Neighbors (KNN)
1️⃣ Choose a value for K (number of neighbors). 2️⃣ Compute the distance between the new data point and all existing points in the dataset (e.g., Euclidean distance). 3️⃣ Select the K closest neighbors. 4️⃣ Make a prediction:
- Classification: Assign the most common class among neighbors (majority voting).
- Regression: Take the average of the target values of the K neighbors.
Choose K:
- Small K (e.g., K=1 or 3):
- ✅ Captures details but can overfit (high variance).
- Large K (e.g., K=10 or 20):
- ✅ More generalization but may underfit (high bias).
- Common practice: Choose K using cross-validation (often √N, where N is the dataset size).
K-Means Clustering
K-means clustering is a popular unsupervised machine learning algorithm that is used to partition a dataset into k clusters. The algorithm works by iteratively assigning instances to the nearest cluster center and updating the cluster centers based on the mean of the instances in each cluster. The goal of k-means clustering is to minimize the sum of squared distances between instances and their respective cluster centers.
Pseudocode for k-means clustering:
- Initialize k cluster centers randomly or using a heuristic.
- Assign each instance to the nearest cluster center.
- Update the cluster centers based on the mean of the instances in each cluster.
- Repeat steps 2 and 3 until convergence.
- Return the final cluster assignments and cluster centers.
K-means clustering is sensitive to the initial cluster centers and can converge to a local minimum. To mitigate this issue, the algorithm is often run multiple times with different initializations, and the best clustering is selected based on a predefined criterion.
Applications of k-means clustering include customer segmentation, image compression, and anomaly detection.
Logistic regression
Sigmoid function:
\[\sigma(z) = \frac{1}{1 + e^{-z}}\]where \(z = wX + b\) is the linear combination of the input features and the model parameters. The nice thing about the sigmoid function is that it maps any real-valued number to the range [0, 1], which is very useful for binary classification.
Cost function:
\[\mathcal{L}(\theta) = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log \hat{y}_i + (1 - y_i) \log (1 - \hat{y}_i) \right]\]where \(\hat{y}_i = \sigma(z_i)\) is the predicted probability of the \(i\)-th sample.
Gradient descent:
\[\nabla_{\theta} \mathcal{L}(\theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)X_i\]Bayesian theorem
Bayesian theorem:
\[P(A \mid B) = \frac{P(B \mid A)P(A)}{P(B)}\]Where \(A\) and \(B\) are events, e.g., A: having a cancer, B: having a positive test result, and \(P(A \mid B)\) is the probability of \(A\) given \(B\). Bayesian theorem can be used to update our belief based on new evidence (given \(B\))
- \(P(A \mid B)\) is the posterior probability of \(A\) given \(B\).
- \(P(B \mid A)\) is the likelihood of \(B\) given \(A\). How likely a patient with cancer (\(A\)) has a positive test result (\(B\)).
- \(P(A)\) is the prior probability of \(A\). The probability of having cancer over all the population.
- \(P(B)\) is the marginal probability of \(B\). The probability of having a positive test result over all the population, including patients with and without cancer.
The marginal probability \(P(B)\) can be computed by summing over all the possible values of \(A\) and usually very expensive to compute because it requires summing over all the possible values of \(A\).
\[P(B) = \sum_{A} P(B \mid A)P(A)\]What is the Naive Bayes classifier?
The Naive Bayes classifier is a simple and efficient machine learning algorithm that is based on Bayes’ theorem and the assumption of conditional independence between features. Despite its simplicity, the Naive Bayes classifier is often used as a baseline model for text classification and other tasks.
The Naive Bayes classifier is particularly well-suited for text classification tasks, such as spam detection and sentiment analysis, where the input features are typically word frequencies or presence/absence of words.
Mathematically, the Naive Bayes classifier predicts the class label of an instance based on the maximum a posteriori (MAP) estimation:
\[\hat{y} = \underset{y \in \mathcal{Y}}{\text{argmax}} P(y|X)\]Where:
- \(\hat{y}\) is the predicted class label.
- \(\mathcal{Y}\) is the set of possible class labels.
- \(X\) is the input features.
- \(P(y \mid X)\) is the posterior probability of class label y given the input features X. The posterior probability \(P(y \mid X)\) is calculated using Bayes’ theorem and the assumption of conditional independence, i.e., \(P(y \mid X) = \frac{P(X \mid y)P(y)}{P(X)}\). The denominator \(P(X)\) is constant for all class labels and can be ignored for the purpose of classification.
-
Curse of dimensionality
The curse of dimensionality refers to the challenges and problems that arise when working with high-dimensional data. As the number of features (dimensions) increases, data becomes sparse, distances become less meaningful, and models struggle to generalize well.
And because distance becomes less meaningful, algorithms that rely on distance such as KNN, SVN, or K-means become less effective.
And because data becomes sparse (but the true pattern is still in lower dimensions), machine learning models need more data to fill in the space, otherwise they will overfit the data.
Overcoming overfitting
L1 vs L2 regularization
Regularization helps prevent overfitting by adding a penalty to the loss function, discouraging overly complex models (large weights or many features used).
L1 regularization:
\[\mathcal{L}(\theta) + \lambda \sum_{i=1}^{n} |\theta_i|\]L2 regularization:
\[\mathcal{L}(\theta) + \lambda \sum_{i=1}^{n} \theta_i^2\]L1 regularization encourages sparsity in the model’s weights (some weights will be exactly 0), while L2 regularization **encourages small weights **(no weight will be exactly 0 but very small).
Because L1 regularization encourages sparsity, it can be used for feature selection (eliminate some features that are not important - set their weights to 0). But it can lead to unstable solutions when features are highly correlated/entangled.
Elastic net regularization is a combination of L1 and L2 regularization.
\[\mathcal{L}(\theta) + \lambda_1 \sum_{i=1}^{n} |\theta_i| + \lambda_2 \sum_{i=1}^{n} \theta_i^2\]Dropout
Dropout is a regularization technique used in neural networks to prevent overfitting by randomly “dropping” (deactivating) neurons during training. This forces the network to learn more robust and generalizable features rather than relying on specific neurons.
🔹 Why? In deep networks, some neurons may become too dependent on others, leading to overfitting. Works well in fully connected layers, less useful in convolutional layers (which have spatial dependencies and less neurons than fully connected layers).
🔹 How? During training, for each mini-batch, some neurons are randomly dropped out with a probability \(p\) (e.g., 0.5). Important thing that most people forget: the remaining neurons need to be scaled up by \(\frac{1}{1-p}\) to keep the expected output the same.
Early stopping
Early stopping is a regularization technique that stops training when the model’s performance on the validation set starts to degrade (model starts to overfit or memorize the training data - therefore, the performance on the validation set starts to decrease).
Batch normalization/layer normalization
Batch Normalization
Batch Normalization normalizes activations across the batch dimension for each feature.
\[\mu = \frac{1}{m} \sum_{i=1}^{m} x_i\] \[\sigma = \sqrt{\frac{1}{m} \sum_{i=1}^{m} (x_i - \mu)^2}\] \[\hat{x}_i = \frac{x_i - \mu}{\sigma}\] \[x_i = \hat{x}_i \cdot \sigma + \mu\]This transformation ensures stable activations, reducing internal covariate shift.
However, batch statistics vary across mini-batches, making it problematic for small batch sizes or RNNs. Therefore, batch normalization is commonly used in CNNs and Fully Connected Networks (FCNs). In inference, we use the running mean and variance to normalize the activations.
Internal Covariate Shift
Internal Covariate Shift occurs when the distribution of activations (features) changes during training due to updates in previous layers. This makes optimization harder because each layer must constantly adapt to new distributions of inputs. It causes slow convergence and unstable training.
It differs from the covariate shift problem, which is the change in the distribution of the input features (e.g., training on sunny images but testing on rainy ones). Internal Covariate Shift happens inside a deep network during training.
Layer Normalization
Layer Normalization normalizes activations across features for each individual data point (sample-wise normalization).
Key Properties:
- Works sample-wise (statistics are computed for each input independently).
- Works well for RNNs and small batch sizes, unlike BatchNorm.
- More stable training in NLP and reinforcement learning tasks.
- Less effective than BatchNorm for CNNs, where spatial dependencies are important.
Data augmentation
Cross-validation
Generalization
Out-of-distribution generalization
Adversarial generalization/training
Sharpness-aware minimization
Evaluation
Metrics
Type I and Type II error
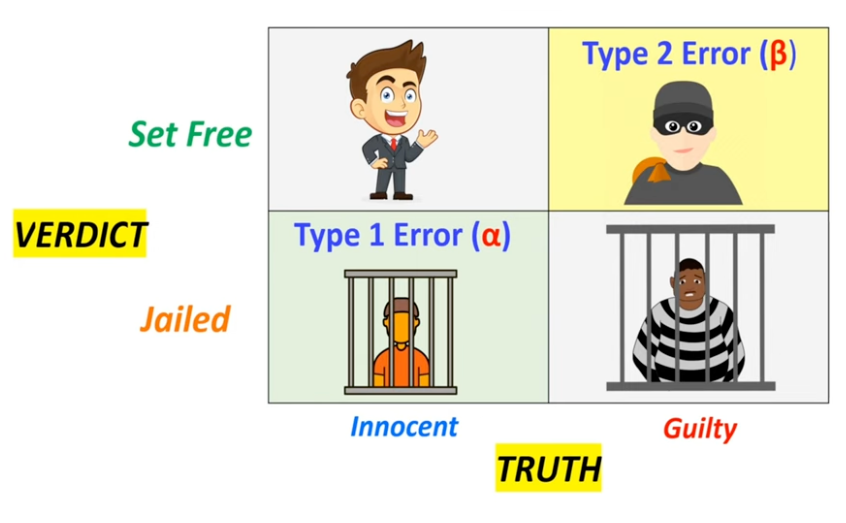
Null hypothesis (H0) is a statement that there is no relationship between two measured phenomena, or no association among groups. It is the default assumption that there is no effect or no difference. The alternative hypothesis (H1) is the statement that there is a relationship between two measured phenomena, or an association among groups. It is the opposite of the null hypothesis.
In the example of Innocent and Guilty, the null hypothesis is “Innocent” and the alternative hypothesis is “Guilty”. Type I error is the incorrect rejection of the null hypothesis (false positive), while Type II error is the failure to reject the null hypothesis when it is false (false negative).
ROC curve
Precision-recall curve
F1 score
AUC
Enjoy Reading This Article?
Here are some more articles you might like to read next: