Erasing Undesirable Concepts in Diffusion Models with Adversarial Preservation

(Shameless plug ) Our other papers on Concept Erasing/Unlearning:

Fantastic Targets for Concept Erasure in Diffusion Models and Where to Find Them,
Tuan-Anh Bui, Trang Vu, Long Vuong, Trung Le, Paul Montague, Tamas Abraham, Dinh Phung
Under Review (Dropbox)

Erasing Undesirable Concepts in Diffusion Models with Adversarial Preservation,
Tuan-Anh Bui, Long Vuong, Khanh Doan, Trung Le, Paul Montague, Tamas Abraham, Dinh Phung
NeurIPS 2024 (arXiv 2410.15618)

Removing Undesirable Concepts in Text-to-Image Generative Models with Learnable Prompts,
Tuan-Anh Bui, Khanh Doan, Trung Le, Paul Montague, Tamas Abraham, Dinh Phung
Preprint (arXiv 2403.12326)

Abstract

Diffusion models excel at generating visually striking content from text but can inadvertently produce undesirable or harmful content when trained on unfiltered internet data. A practical solution is to selectively removing target concepts from the model, but this may impact the remaining concepts. Prior approaches have tried to balance this by introducing a loss term to preserve neutral content or a regularization term to minimize changes in the model parameters, yet resolving this trade-off remains challenging. In this work, we propose to identify and preserving concepts most affected by parameter changes, termed as adversarial concepts. This approach ensures stable erasure with minimal impact on the other concepts. We demonstrate the effectiveness of our method using the Stable Diffusion model, showing that it outperforms state-of-the-art erasure methods in eliminating unwanted content while maintaining the integrity of other unrelated elements.

Key Observations and Motivations

(1) Erasing different target concepts from text-to-image diffusion models leads to varying impacts on the remaining concepts. For instance, removing ‘nudity’ significantly affects related concepts like ‘women’ and ‘men’ but has minimal impact on unrelated concepts like ‘garbage truck.’ (2) Neutral concepts lie in the middle of the sensitivity spectrum, suggesting that they do not adequately represent the model’s capability to be preserved. (3) Furthermore, the choice of concept to be preserved during erasure significantly impacts the model’s generative capability; relying on neutral concepts, as in previous work, is not an optimal solution. (4) This highlights the need for adaptive methods to identify and preserve the most sensitive concepts related to the target concept being erased, rather than relying on fixed neutral/generic concepts.

Naive Concept Erasure

There are two main tasks in concept erasure: (1) removing unwanted concepts and (2) preserving the remaining concepts so that the model’s generative capability is not impaired. The first task can be achieved by simply mapping the unwanted concept to a neutral concept such as “a photo” or empty string, which can be formulated as the following optimization problem:

where \(\epsilon_{\theta}\) and \(\epsilon_{\theta^{'}}\) are the denoising diffusion models with the original foundation model \(\theta\) and the sanitized model \(\theta^{'}\), respectively. \(c_e\) and \(c_n\) are the unwanted and neutral concepts.

Therefore, most existing methods focus on the second task, either by introducing a loss term to preserve neutral content [1,2]

or a regularization term to minimize changes in the model parameters [3,4] \(\begin{equation} L = \left\| \theta^{'} - \theta \right\|_2^2 \end{equation}\).

However, there is a lack of understanding on how the removal of a concept affects the model’s generative capability.

Impact of Concept Removal on the Model Performance

We here approach the problem more carefully via a study on the impact of erasing a specific concept on model performance on the remaining ones. More importantly, we are concerned with the most sensitive concepts to erasure.

For example, when removing the concept of “nudity”, we are curious to know which concepts change the most in the model’s output, so that we can preserve these concepts specifically to ensure the model’s capability is maintained, at least with respect to these concepts.

We observe the following phenomenons:

(1) The Removal of Different Target Concepts Leads to Different Side-Effects.

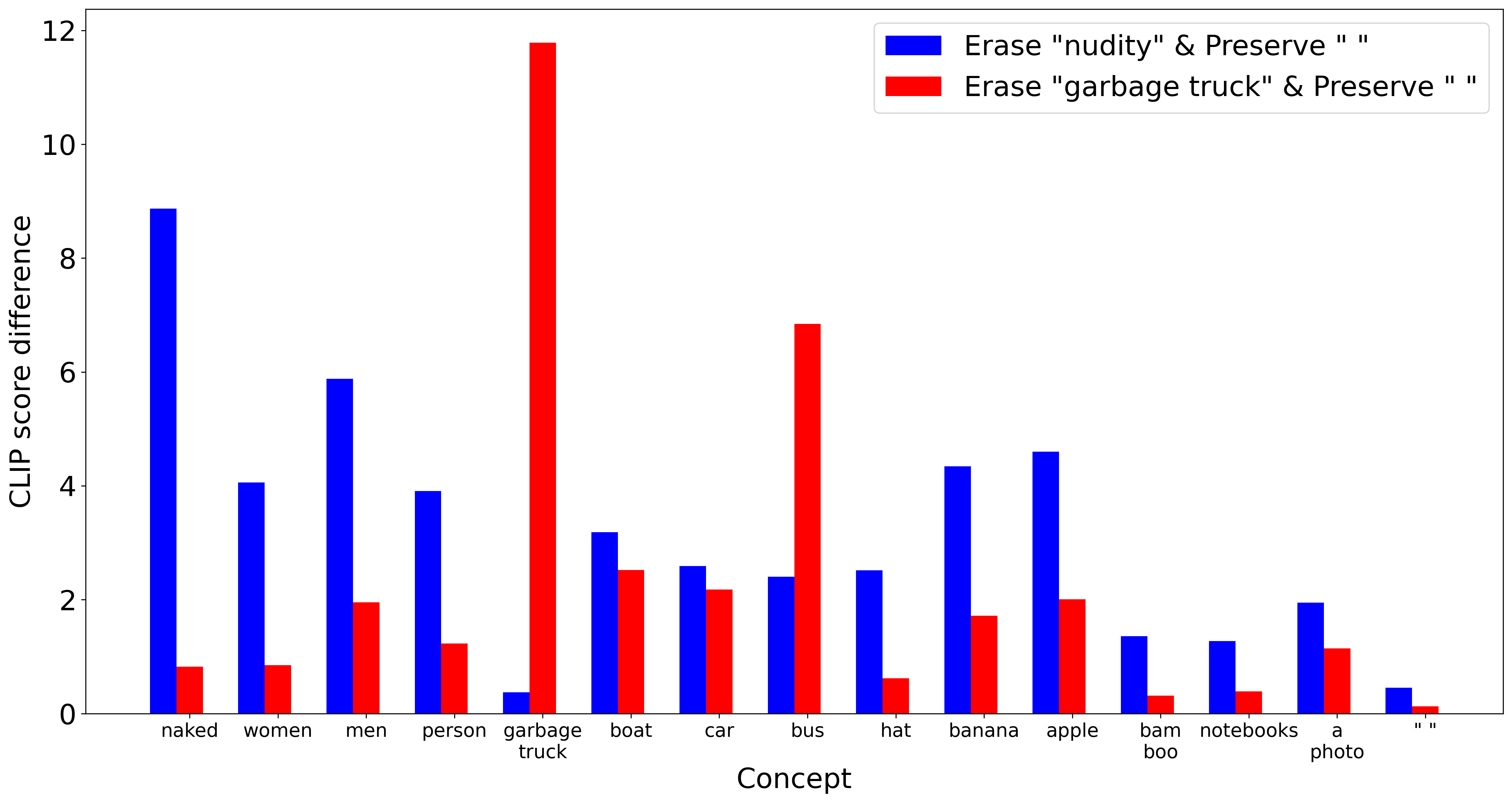
Figure above shows the impact of the removal of two distinct concepts, “nudity” and “garbage truck”, on other concepts, measured by the difference of the CLIP score, \(\delta_{\text{'nudity'}}(c), \delta_{\text{'garbage truck'}}(c)\). A larger \(\delta(c)\) indicates a greater negative impact on the model’s ability to generate concept \(c\).

It can be seen that removing the “nudity” concept significantly affects highly related concepts such as “naked”, “men”, “women”, and “person”, while having minimal impact on unrelated concepts such as “garbage truck”, ‘bamboo’ or neutral concepts such as “a photo” or the null “ “ concept.

Similarly, removing the “garbage truck” concept significantly reduces the model’s capability on concepts like “boat”, “car”, “bus”, while also having little impact on other unrelated concepts such as “naked”, “women” or neutral concepts.

These results suggest that removing different target concepts leads to varying impacts on other concepts. This indicates the need for an adaptive method to identify the most sensitive concepts relative to a particular target concept, rather than relying on random or fixed concepts for preservation. Moreover, in both cases, neutral concepts like “a photo” or the null concept show resilience and independence from changes in the model’s parameters, suggesting that they do not adequately represent the model’s capability to be preserved.

(2) Neutral Concepts lie in the Middle of the Sensitivity Spectrum.

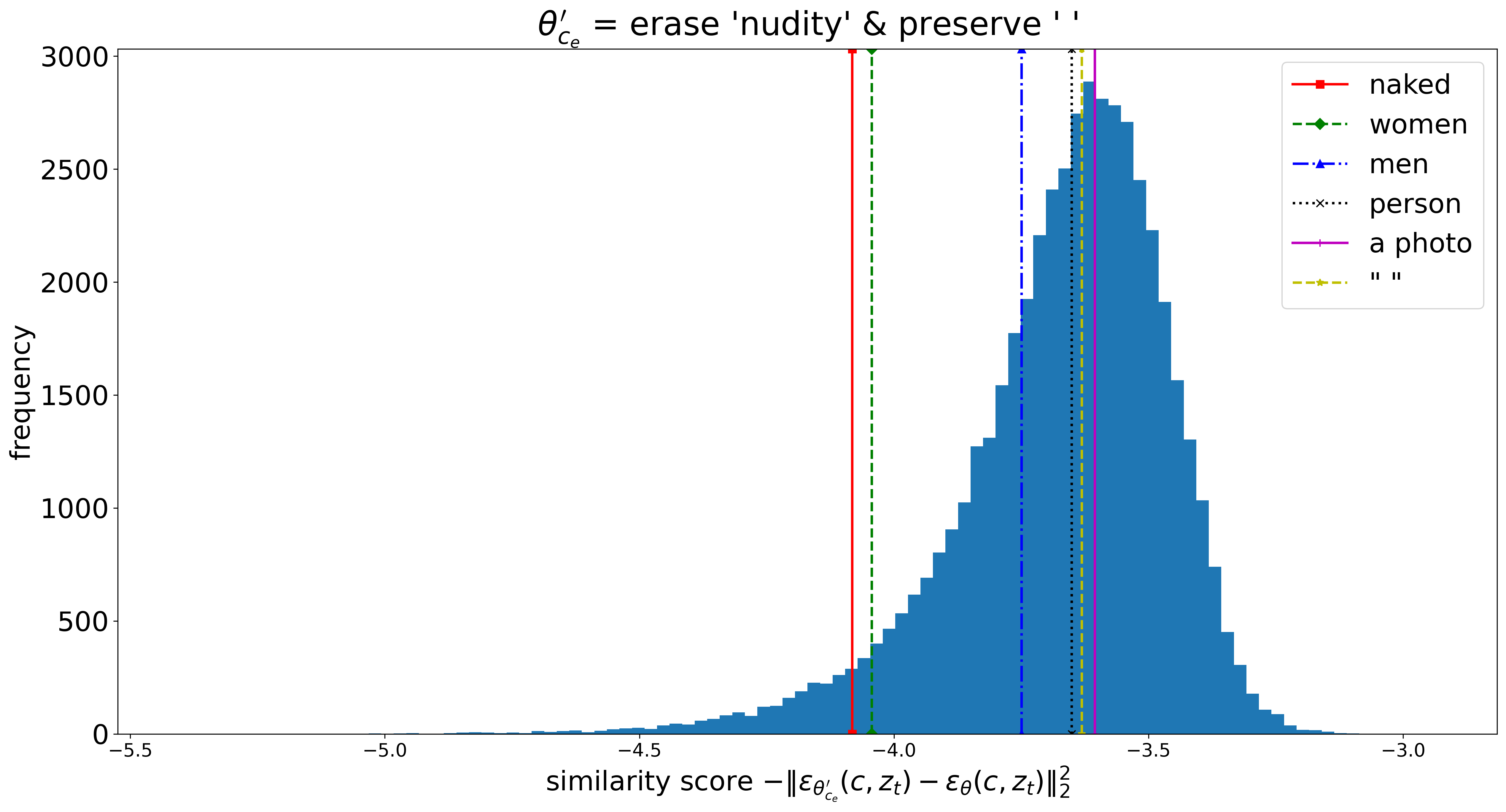
Figure above shows the distribution of similarity scores between the outputs of the original model \(\theta\) and the sanitized model \(\theta_{c_e}'\) for each concept \(c\) from the CLIP tokenizer vocabulary.

The histogram reveals that the similarity scores span a wide range, indicating that the impact of unlearning the target concept on generating other concepts varies significantly. The lower the similarity score, the more different the outputs of the two models are, and the more sensitive the concept is to the target concept. Notably, the more related concepts like “women” or “men” are more sensitive to the removal of “nudity” than many neutral concepts that lie in the middle of the sensitivity spectrum.

(3)What Concept should be Kept to Maintain Model Performance?

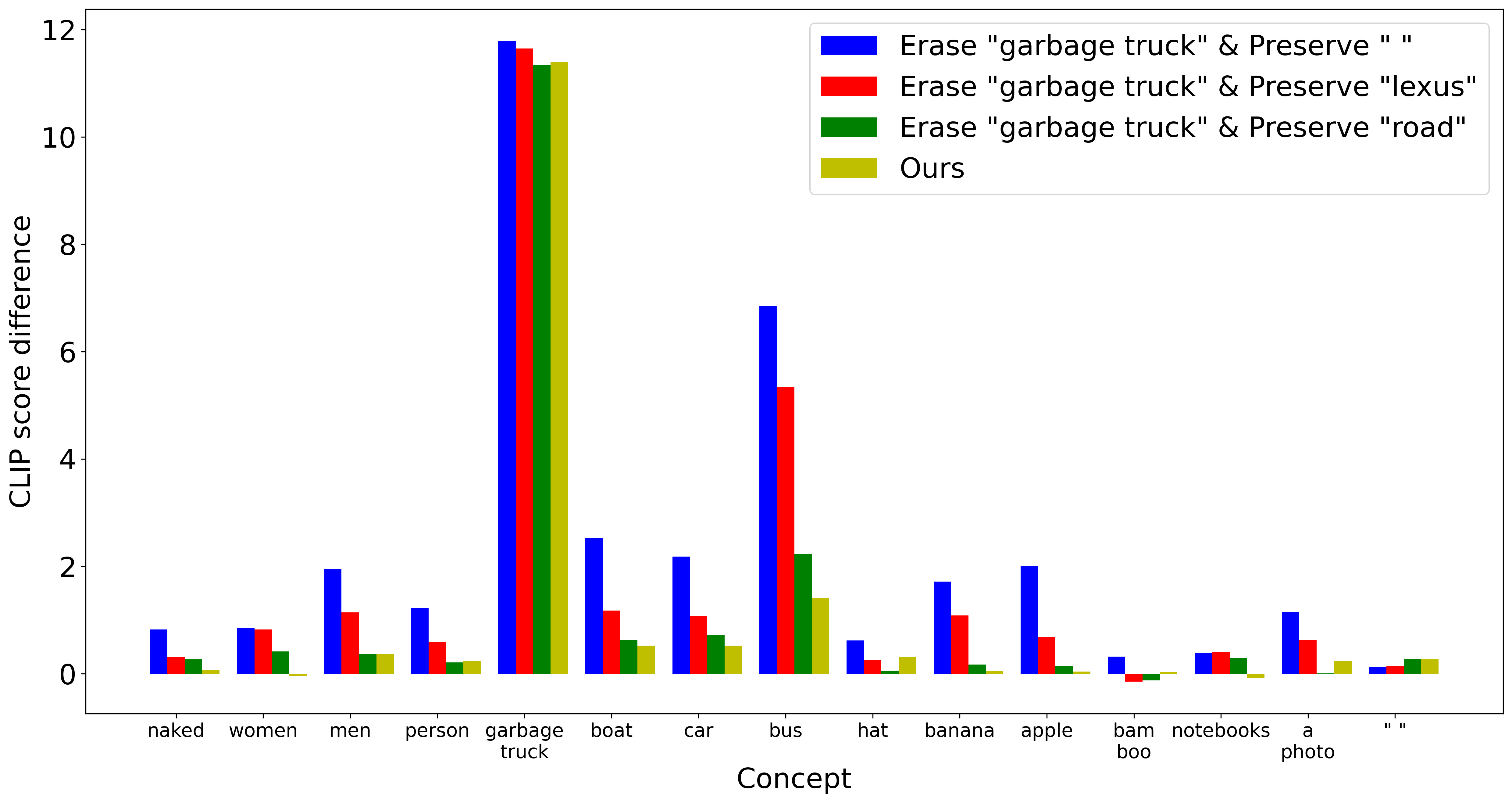
Figure above presents the results of an experiment similar to the previous one, with one key difference: we utilize the prior knowledge gained from the previous experiment. Specifically, when erasing the “garbage truck”, we apply different preservation strategies, including preserving a fixed concept such as “ “, “lexus”, or “road”, and adaptively preserving the most sensitive concept found by our method.

The results show that with simple preservation strategies such as preserving a fixed but related concept like “road”, the model’s capability on other concepts is better maintained compared to preserving a neutral concept. However, the results of adaptively preserving the most sensitive concept show the best performance, with the least side effects on other concepts.

Our Approach - Adversarial Preservation

Motivated by the observations in the previous section, our approach involves identifying the most sensitive concepts related to a specific target concept. For example, when removing the concept of nudity, we identify which concepts are most affected in the model’s output so that we can specifically preserve these concepts to ensure the model’s capability is maintained.

In each iteration, before updating the model parameters, we first identify the concept \(c_a\) that is most sensitive to changes in the model parameters as we work to remove the target concepts.

where \(\lambda >0\) is a parameter and \(\mathcal{R}=\mathcal{C}\setminus\mathbf{E}\) denotes the remaining concepts.

Objective loss \(L_1\) is the same as in the naive approach, aiming to erase the target concept \(c_e\) by forcing its output to match that of a neutral concept. Our main contribution lies in the introduction of the adversarial preservation loss \(L_2\), which aims to identify the most sensitive concept \(c_a\) that is most affected by changes in the model parameters when removing the target concepts.

Challenges of Searching in Continuous Space for Adversarial Concepts

Since the concepts exist in a discrete space, the straightforward approach would involve revisiting all concepts in \(\mathcal{R}\), resulting in significant computational complexity. Another naive approach is to consider the concepts as lying in a continuous space and use the Projected Gradient Descent (PGD) method [5] to search within the local region of the continuous space of the concepts.

More specifically, we initialize the adversarial prompt with the text embedding of the to-be-erased concept, e.g., \(c_{a,0}=c_e=\tau({\text{"Garbage Truck"}})\), and then update the adversarial concept with gradient \(\nabla_{c_a} L_2\).

Interestingly, while this approach provides an efficient computational method, we find that the adversarial concept quickly collapses from the initial concept to a background concept with the color information of the object as shown in the first row of Figure below.

This can be explained by the fact that while the concepts lie in a discrete space, their embeddings lie in a continuous space \(R^d\) and the gradient of the loss function \(L_2\) is computed in this continuous space. Therefore, the update step \(c_{a,t+1} = c_{a,t} + \eta \nabla_{c_a} L_2\) moves the embedding of \(c_a\) towards the direction of the gradient, which is unlikely to be one of the discrete concepts.

To combine the benefits of both approaches—making the process continuous and differentiable for efficient training while achieving meaningful concepts that are related to the target concept (second row of above Figure)— we first define a distribution over the discrete concept embedding vector space as \(\mathbb{P}_{\mathcal{R},\pi}=\sum_{i=1}^{\left | \mathcal{R} \right |}\pi_{i}\delta_{e_{i}}\) with the Dirac delta function \(\delta\) and the weights \(\pi\in\Delta_{\mathcal{R}}= \{\pi'\geq \boldsymbol{0}: \Vert \pi'\Vert_1 =1\}\). Instead of directly searching for the most sensitive concept \(c_a\) in the discrete concept embedding vector space \(\mathcal{R}\), we switch to searching for the embedding distribution \(\pi\) on the simplex \(\Delta_{\mathcal{R}}\) and subsequently transform it back into a discrete space using the temperature-dependent GumbelSoftmax trick [6] as follows:

where \(\lambda >0\) is a parameter, \(\mathbf{G}\) is Gumbel-Softmax operator and \(\odot\) is element wise multiplication operator. The pseudo-algorithm involves a two-step optimization process, outlined in Algorithm 1,2 in the paper.

Experiments

We conducted comprehensive experiments on three erasure tasks to demonstrate the effectiveness of our method. Please refer to the paper for more details.

Beside the experiments that support the superiority of our method (of course as all other papers :D), in this blog post (with more relaxed style), we would like to emphasize some interesting observations that has been discussed in Appendix B of our paper that we think are worthy of future research.

Collapsed Concepts

As discussed in Appendix B.4, we provide intermediate results of the adversarial concept search process. More specifically, we visualize the images generated by \(c_a\) and \(c_e\) at different steps of the search process.

As shown in the even rows, we observe that the model gradually removes the to-be-erased objects from the generated images as the fine-tuning steps increase. Interestingly, these to-be-erased concepts tend to collapse into the same concept, even though they started from different concepts.

For example, the “Garbage truck” and “Cassette player” in the \(2^\text{nd}\) and \(4^\text{th}\) rows eventually transform into a background-like image in the last column. This can be explained by the fact that in the objective function, the erasing loss uses the same null concept \(c_n\) for all to-be-erased concepts, which encourages the model to remove them simultaneously, eventually leading to the collapse of these concepts into the same form.

Our follow-up work [6] has investigated the phenomenon of collapsed concepts and proposes a method to address it. Please check it out for more details.

Difficulties in Searching for Adversarial Concepts

As discussed in Appendix B.5, we we provide empirical examples to show that finding the most sensitive concept \(c_a\) is not always straightforward when using heuristic methods, which further emphasizes the advantage of our method.

Can we use the similarity in the textual embedding space to find the most sensitive concept?

Large pretrained multimodal models like CLIP have been widely used for zero-shot learning because their textual embedding space is highly correlated with the visual space. Intuitively, one might think that the similarity between the target concept \(c_e\) and other concepts in the textual embedding space can help identify the most sensitive concept \(c_a\). For example, the closer a concept \(c_i\) is to the target concept \(c_e\) in the textual embedding space, the more likely it is to be the most sensitive concept \(c_a\). However, we demonstrate that this heuristic method is not always effective.

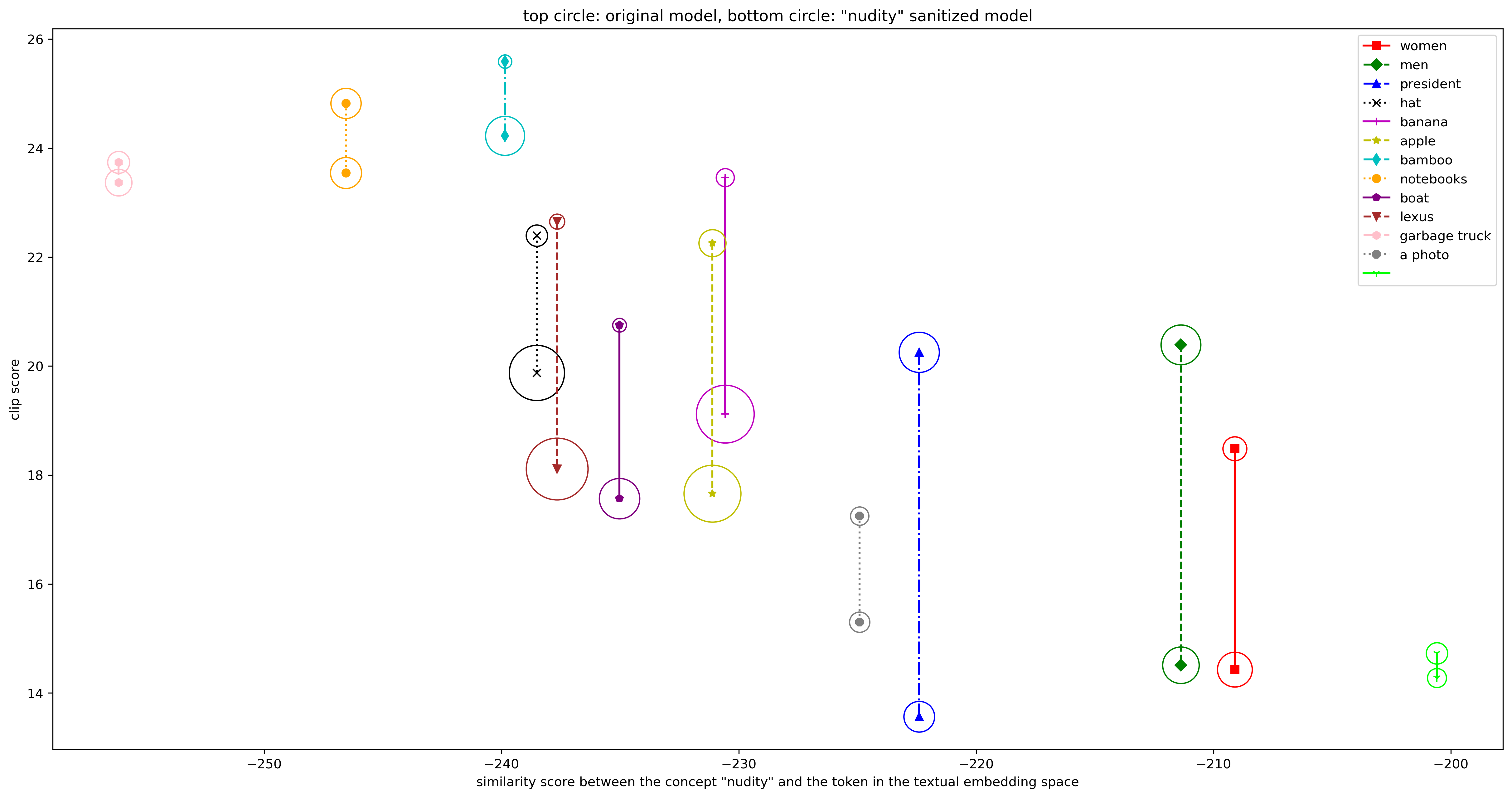
Figure below shows the correlation between the drop in the CLIP scores between the base/original model and the sanitized model (i.e., after removing the target concept “nudity”) and the similarity score between the target concept “nudity” and other concepts in the textual embedding space.

It can be seen that the above intuition does not always hold, as the similarity score does not correlate with the drop in the CLIP scores. For example, except for the concept “naked”, the null concept is the most similar to “nudity” in the textual embedding space, but it experiences the lowest drop in CLIP scores. On the other hand, two concepts, “a photo” and “president”, are close in the textual embedding space but are affected differently during the erasing process. This demonstrates that similarity in the textual embedding space is not an appropriate metric for identifying the most sensitive concept in this context.

Discussion on Metrics to Measure the Erasure Performance

One of the main challenges in developing erasure methods is the lack of a proper metric to measure erasure performance. Specifically, performance is evaluated by how well the model forgets the target concept while retaining other concepts. This raises a critical question: how can we validate whether a concept is present in a generated image? Although this may seem like a simple task, it is quite challenging due to the vast number of concepts that generative models can produce. It is infeasible to have a classification model capable of detecting all possible concepts.

While the FID score is a commonly used metric to assess the generative quality of models, it may not be sufficient for evaluating erasure performance. To the best of our knowledge, the CLIP alignment score is the most suitable existing metric for measuring concept inclusion. However, it is not without limitations. For example, CLIP’s training set does not include NSFW content, making it less reliable for detecting such concepts. We believe that a more comprehensive evaluation metric is still lacking and that developing one would be a valuable direction for future research.

Limitations

• A crucial aspect of our method is the concept space \(\mathcal{R}\), where we search for the most sensitive concept \(c_a\). In our experiments, we use two vocabularies: the CLIP token vocabulary, which includes 49,408 tokens, and the Oxford 3000 word list, comprising the 3000 most common English words. While the CLIP token vocabulary is more comprehensive, it presents challenges due to the large number of nonsensical tokens. Therefore, we use the Oxford 3000-word list to demonstrate the effectiveness of our method in all experiments. However, as revealed later in our follow-up work, the better well-curated concept space can further improve the performance of our method.

• To search for the adversarial concept \(c_a\) effectively, we employ the Gumbel-Softmax trick to sample from the categorical distribution in the concept space \(\mathcal{R}\). This approach requires feeding the model with the embeddings of the entire concept space \(\mathcal{R}\), which exponentially increases the computational cost as the size of the concept space grows. To mitigate this, we use a subset of the \(K\) most similar concepts to the target concept \(c_e\) to reduce computational costs. The similarity between concepts is calculated using cosine similarity between their embeddings.

Citation

If you find this work useful in your research, please consider citing our paper (or our other papers ):

@article{bui2024erasing,
  title={Erasing Undesirable Concepts in Diffusion Models with Adversarial Preservation},
  author={Bui, Anh and Vuong, Long and Doan, Khanh and Le, Trung and Montague, Paul and Abraham, Tamas and Phung, Dinh},
  booktitle={NeurIPS},
  year={2024}
}

@article{bui2024adaptive,
  title={Fantastic Targets for Concept Erasure in Diffusion Models and Where to Find Them},
  author={Bui, Anh and Vu, Trang and Vuong, Long and Le, Trung and Montague, Paul and Abraham, Tamas and Phung, Dinh},
  journal={Preprint},
  year={2024}
}

@article{bui2024removing,
  title={Removing Undesirable Concepts in Text-to-Image Generative Models with Learnable Prompts},
  author={Bui, Anh and Doan, Khanh and Le, Trung and Montague, Paul and Abraham, Tamas and Phung, Dinh},
  journal={arXiv preprint arXiv:2403.12326},
  year={2024}
}

References

[1] Rohit Gandikota et al. Erasing concepts from diffusion models. ICCV, 2023.

[2] Bui, Anh, et al. Removing Undesirable Concepts in Text-to-Image Generative Models with Learnable Prompts. arXiv preprint arXiv:2403.12326, 2024.

[3] Eric Zhang et al. Forget-me-not: Learning to forget in text-to-image diffusion models. arXiv preprint arXiv:2303.17591, 2023.

[4] Hadas Orgad, Bahjat Kawar, and Yonatan Belinkov. Editing implicit assumptions in text-to-image diffusion models. In IEEE International Conference on Computer Vision, ICCV 2023.

[5] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083, 2017.

[6] Bui, Anh, et al. Fantastic Targets for Concept Erasure in Diffusion Models and Where To Find Them. Under review.