DNA Series - Part 2 - Array
- 1. Two Sum
- 121. Best Time to Buy and Sell Stock
- 217. Contains Duplicate
- 238. Product of Array Except Self
- 53. Maximum Subarray
- 152. Maximum Product Subarray
- 153. Find Minimum in Rotated Sorted Array
- 33. Search in Rotated Sorted Array
- 15. 3Sum
- 11. Container With Most Water
- 70. Climbing Stairs
- 322. Coin Change
- 300. Longest Increasing Subsequence
- 139. Word Break
- 377. Combination Sum IV
- 198. House Robber
- 213. House Robber II
- 62. Unique Paths
- 55. Jump Game
- 133. Clone Graph
- 207. Course Schedule
- 417. Pacific Atlantic Water Flow
- 200. Number of Islands
- 212. Word Search II
- 73. Set Matrix Zeroes
- 54. Spiral Matrix
- 392. Is Subsequence
- 338. Counting Bits
- 746. Min Cost Climbing Stairs
- 191. Number of 1 Bits
- 268. Missing Number
- 1143. Longest Common Subsequence
- 91. Decode Ways
- 39. Combination Sum
- 90. Subsets II
- 46. Permutations
- 257. Binary Tree Paths
- 51. N-Queens
- 17. Letter Combinations of a Phone Number
- 77. Combinations
- 22. Generate Parentheses
- 79. Word Search
- 120. Triangle
- 64. Minimum Path Sum
- 63. Unique Paths II
- 5. Longest Palindromic Substring
- Reflection
In this project, I will try to solve 75 Leetcode questions as listed in this link.
1. Two Sum
DescriptionGiven an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
Example 1:
Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Output: Because nums[0] + nums[1] == 9, we return [0, 1].
Example 2:
Input: nums = [3,2,4], target = 6
Output: [1,2]
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
dic = {}
for i, num in enumerate(nums):
if num in dic:
return [dic[num], i]
else:
dic[target - num] = i
121. Best Time to Buy and Sell Stock
DescriptionYou are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
Example 1:
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
Example 2:
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.
Two pointers starting from both ends (i.e., move left or right pointer based on which side has a better profit)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
l, r = 0, len(prices)-1
minL = prices[l]
maxR = prices[r]
while l<r:
if prices[l] < minL:
minL = prices[l]
if prices[r] > maxR:
maxR = prices[r]
if prices[r-1] - minL > maxR - prices[l+1]:
r -= 1
else:
l += 1
return maxR - minL if maxR >= minL else 0
Two pointers starting from right (i.e., find highest price and then find the lowest price before it, fastest solution)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
max_profit = 0
max_price = 0
for i in range(len(prices)-1, -1, -1):
if prices[i] > max_price:
max_price = prices[i]
else:
max_profit = max(max_profit, max_price - prices[i])
return max_profit
Two pointers starting from left (i.e., find lowest price and then find the highest price after it)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
min_price = float('inf')
max_profit = 0
for i in range(len(prices)):
if prices[i] < min_price:
min_price = prices[i]
else:
max_profit = max(max_profit, prices[i] - min_price)
return max_profit
217. Contains Duplicate
DescriptionGiven an integer array nums, return true if any value appears at least twice in the array, and return false if every element is distinct.
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
dic = {}
for num in nums:
if num in dic:
return True
else:
dic[num] = 1
238. Product of Array Except Self
DescriptionGiven an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].
The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
You must write an algorithm that runs in O(n) time and without using the division operation.
Example 1:
Input: nums = [1,2,3,4]
Output: [24,12,8,6]
Example 2:
Input: nums = [-1,1,0,-3,3]
Output: [0,0,9,0,0]
We will use two arrays to store the product of all elements to the left and right of each element. Then, we will multiply the two arrays to get the final result.
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
left = [1] * len(nums)
right = [1] * len(nums)
for i in range(1, len(nums)):
left[i] = left[i-1] * nums[i-1]
right[len(nums)-1-i] = right[len(nums)-i] * nums[len(nums)-i]
return [left[i] * right[i] for i in range(len(nums))]
53. Maximum Subarray
DescriptionGiven an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
A subarray is a contiguous part of an array.
Example 1:
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Example 2:
Input: nums = [1]
Output: 1
Example 3:
Input: nums = [5,4,-1,7,8]
Output: 23
Use Kadane’s algorithm to find the maximum subarray sum. The idea is to keep track of the maximum sum of subarrays ending at each index. If the sum is negative, we reset it to 0. Refer to this video and https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/ article for more details.
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
res = nums[0]
accsum = nums[0]
for n in nums[1:]:
accsum += n
if accsum <= n:
accsum = n
if accsum >= res:
res = accsum
return res
Dynamic programming solution (from greeksforgeeks)
Observation: DP[i] = max(DP[i-1] + nums[i], nums[i])
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
DP = [0] * len(nums)
DP[0] = nums[0]
for i in range(1, len(nums)):
DP[i] = max(DP[i-1] + nums[i], nums[i])
return max(DP)
152. Maximum Product Subarray
DescriptionGiven an integer array nums, find a contiguous non-empty subarray within the array that has the largest product, and return the product.
It is guaranteed that the answer will fit in a 32-bit integer.
Example 1:
Input: nums = [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
Example 2:
Input: nums = [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.
Example 3:
Input: nums = [-2,3,-4]
Output: 24
Explanation: The result is 24 because (-2)*3*(-4) = 24.
Observation:
- It is not the same as the maximum subarray sum. It is because the product of two negative numbers is positive.
- We need to keep track of the maximum and minimum product so far.
- cumMax = max(cumMax * n, cumMin * n, n)
- cumMin = min(cumMax * n, cumMin * n, n)
- res = max(res, cumMax)
- We need to reset cumMax and cumMin when we encounter a 0.
class Solution:
def maxProduct(self, nums: List[int]) -> int:
dp_max = [1] * len(nums)
dp_min = [1] * len(nums)
dp_max[0] = nums[0]
dp_min[0] = nums[0]
for i in range(1, len(nums)):
if nums[i] == 0:
dp_max[i] = 0
dp_min[i] = 0
continue
cur = [dp_max[i-1] * nums[i], dp_min[i-1] * nums[i], nums[i]]
dp_max[i] = max(cur)
dp_min[i] = min(cur)
return max(dp_max)
class Solution:
def maxProduct(self, nums: List[int]) -> int:
res = max(nums)
cumMax = 1
cumMin = 1
for n in nums:
if n == 0:
cumMax = 1
cumMin = 1
continue
temp = max(cumMax * n, cumMin * n, n)
cumMin = min(cumMax * n, cumMin * n, n)
cumMax = temp
res = max(res, cumMax)
return res
153. Find Minimum in Rotated Sorted Array
DescriptionSuppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
-
[4,5,6,7,0,1,2]if it was rotated4times. -
[0,1,2,4,5,6,7]if it was rotated7times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this array.
You must write an algorithm that runs in O(log n) time.
Example 1:
Input: nums = [3,4,5,1,2]
Output: 1
Explanation: The original array was [1,2,3,4,5] rotated 3 times.
Example 2:
Input: nums = [4,5,6,7,0,1,2]
Output: 0
Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times.
Example 3:
Input: nums = [11,13,15,17]
Output: 11
Explanation: The original array was [11,13,15,17] and it was rotated 4 times.
We can use binary search to find the minimum element.
- if nums[left] < nums[right], then nums[left] is the minimum element.
- if nums[mid] > nums[right], then the minimum element is in the right half.
- if nums[mid] < nums[right], then the minimum element is in the left half.
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums)-1
if nums[left] < nums[right]:
return nums[left]
while left < right:
mid = (left + right) // 2
if nums[mid] > nums[right]:
left = mid + 1
else:
right = mid
return nums[left]
33. Search in Rotated Sorted Array
DescriptionThere is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums after the rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums)-1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] >= nums[left]:
if nums[left] <= target < nums[mid]:
right = mid -1
else:
left = mid + 1
else:
if nums[mid] < target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
15. 3Sum
DescriptionGiven an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
Example 1:
Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
Example 2:
Input: nums = [0,1,1]
Output: []
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
if len(nums) == 3:
return [nums] if sum(nums) == 0 else []
nums.sort()
n = len(nums)
res = []
for i in range(n):
if i > 0 and nums[i] == nums[i-1]:
continue
left, right = i+1, n-1
while left < right:
sum3 = nums[i] + nums[left] + nums[right]
if sum3 == 0:
res.append([nums[i], nums[left], nums[right]])
left += 1
right -= 1
while left < right and nums[left] == nums[left-1]:
left += 1
while left < right and nums[right] == nums[right+1]:
right -= 1
elif sum3 < 0:
left += 1
else:
right -= 1
return res
11. Container With Most Water
DescriptionGiven n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.
Notice that you may not slant the container.
Example 1:
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1]
Output: 1
class Solution:
def maxArea(self, height: List[int]) -> int:
left, right = 0, len(height)-1
res = 0
while left < right:
res = max(res, min(height[left], height[right]) * (right - left))
if height[left] < height[right]:
left += 1
else:
right -= 1
return res
70. Climbing Stairs
DescriptionYou are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
Key Observation: DP[i] = DP[i-1] + DP[i-2] which means the number of ways to reach the i-th step is the sum of the number of ways to reach the (i-1)-th step and the number of ways to reach the (i-2)-th step.
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
a, b = 1, 2
for _ in range(2, n):
a, b = b, a+b
return b
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
dp = [0] * (n+1)
dp[0] = 1
dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
322. Coin Change
DescriptionYou are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
Example 1:
Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1
Key Observation: DP[i] = min(DP[i-c1], DP[i-c2], ...) + 1 which means the minimum number of coins to make up the amount i is the minimum number of coins to make up the amount i-c1, i-c2, … plus 1.
This problem can be visualized as a tree with the root node as the amount and the children nodes as the amount - coin values. The problem is to find the shortest path from the root to the target amount.
def coinChange(self, coins: List[int], amount: int) -> int:
BIG_NUM = amount + 1
dp = [BIG_NUM] * (amount+1)
if amount == 0:
return 0
dp[0] = 0
for i in range(0,amount+1):
for c in coins:
if i + c <= amount:
dp[i+c] = min(dp[i] + 1,dp[i+c])
if dp[amount] == BIG_NUM:
return -1
else:
return dp[amount]
300. Longest Increasing Subsequence
Given an integer array nums, return the length of the longest strictly increasing subsequence.
A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].
Example 1:
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Example 2:
Input: nums = [0,1,0,3,2,3]
Output: 4
Key Observation:
- When considering the i-th element, we need to find the longest increasing subsequence that ends with
nums[i]. - Straightforward case is when nums[i] is the largest element, then the longest `dp[i] = dp[i-1] + 1
- The addition of nums[i] to the subsequence causes the change of all previous
dp[j]wherenums[j] < nums[i].
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
dp = [1] * n
for i in range(n-2,-1,-1):
for j in range(i+1,n,1):
if nums[i] < nums[j]:
dp[i] = max(dp[i], dp[j]+1)
return max(dp)
139. Word Break
Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.
Note that the same word in the dictionary may be reused multiple times in the segmentation.
Example 1:
Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Example 2:
Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Example 3:
Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
n = len(s)
dp = [False] * (n + 1)
dp[-1] = True
for i in range(n-1, -1, -1):
for w in wordDict:
# check whether the word w in the head of the sub string s
if len(w) <= len(s[i:]):
if w == s[i:i+len(w)]:
dp[i] = any([dp[i+len(w)], dp[i]])
return dp[0]
377. Combination Sum IV
Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.
The test cases are generated so that the answer can fit in a 32-bit integer.
Example 1:
Input: nums = [1,2,3], target = 4
Output: 7
Explanation:
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3, 1)
(2, 1, 1)
(2, 2, 1)
(3, 1, 1)
Example 2:
Input: nums = [9], target = 3
Output: 0
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1)
dp[0] = 1
for i in range(target+1):
for num in nums:
if i + num <= target:
dp[i+num] = dp[i+num] + dp[i]
return dp[-1]
198. House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 2:
Input: nums = [2,7,9,3,1]
Output: 12
Observation:
- We can either rob the current house or not.
- If we rob the current house, we cannot rob the previous house.
- If we do not rob the current house, we can rob the previous house.
- dp[i] = max(dp[i-1], dp[i-2] + nums[i])
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) <= 2:
return max(nums)
dp = [0] * len(nums)
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, len(nums)):
dp[i] = max(dp[i-1], dp[i-2] + nums[i])
return dp[-1]
def rob(self, nums: List[int]) -> int:
cur, pre = 0, 0
# [pre, cur, n, n+1, ...]
for n in nums:
temp = max(pre + n, cur)
pre = cur
cur = temp
return cur
213. House Robber II
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
Observation:
- We can apply the same solution as the previous problem, and compare between two cases: - rob the first house, not the last house - not rob the first house, rob the last house
class Solution:
def rob(self, nums: List[int]) -> int:
def _rob(nums):
dp = [0] * len(nums)
if len(nums) <= 2:
return max(nums)
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, len(nums)):
dp[i] = max(dp[i-1], dp[i-2] + nums[i])
return dp[-1]
if len(nums)== 1:
return nums[0]
return max(_rob(nums[:-1]), _rob(nums[1:]))
def rob(self, nums: List[int]) -> int:
def _rob(nums):
cur, pre = 0, 0
# [pre, cur, n, n+1, ...]
for n in nums:
temp = max(pre + n, cur)
pre = cur
cur = temp
return cur
if len(nums)== 1:
return nums[0]
return max(_rob(nums[:-1]), _rob(nums[1:]))
62. Unique Paths
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m-1][n-1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
Example 1:
Input: m = 3, n = 7
Output: 28
def uniquePaths(self, m: int, n: int) -> int:
grid = [[0 for _ in range(n)] for _ in range(m)]
# set the last row and last col to be 1
for i in range(n):
grid[m-1][i] = 1
for i in range(m):
grid[i][n-1] = 1
for row in range(m-2, -1, -1):
for col in range(n-2, -1, -1):
grid[row][col] = grid[row][col+1] + grid[row+1][col]
return grid[0][0]
55. Jump Game
You are given an integer array nums. You are initially positioned at the array’s first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
Example 1:
Input: nums = [2,3,1,1,4]
Output: true
def canJump(self, nums: List[int]) -> bool:
dp = [False] * len(nums)
dp[-1] = True
for i in range(len(nums)-2,-1,-1): # start at len(nums)-2, stop at 0
# any(dp[i + 0], dp[i + 1], ..., dp[i + nums[i]])
furthest = min(i + nums[i], len(nums)) + 1
dp[i] = any(dp[i:furthest])
return dp[0]
133. Clone Graph
Given a reference of a node in a connected undirected graph, return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case:
- An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
Example 1:
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
207. Course Schedule
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
def canFinish(numCourses: int, prerequisites: List[List[int]]) -> bool:
mapPre = {c:[] for c in range(numCourses)}
for c, p in prerequisites:
mapPre[c].append(p)
visited = {}
def dfs(c):
res = []
if mapPre[c] == []:
return True
visited[c] = True
for p in mapPre[c]:
if p in visited:
return False
else:
res.append(dfs(p))
mapPre[c] = []
del visited[c]
return all(res)
res = [dfs(c) for c,p in prerequisites]
return all(res)
417. Pacific Atlantic Water Flow
There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island’s left and top edges, and the Atlantic Ocean touches the island’s right and bottom edges.
The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).
The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell’s height is less than or equal to the current cell’s height. Water can flow from any cell adjacent to an ocean into the ocean.
Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.
Example 1:
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
class Solution:
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
m = len(heights)
n = len(heights[0])
po_map = [[0 for _ in range(n)] for _ in range(m)]
ao_map = [[0 for _ in range(n)] for _ in range(m)]
po_map[0] = [1 for _ in range(n)]
ao_map[-1] = [1 for _ in range(n)]
for i in range(m):
po_map[i][0] = 1
ao_map[i][-1] = 1
def valid(r, c):
if r < 0 or r >= m:
return False
if c < 0 or c >= n:
return False
return True
def reverse_flow(r,c, flow_map):
# going reverse flow
# if lower --> stop
# if higher --> mark as 1, mark as visited
# directions [up, down, left, right]
ds = [[-1,0], [1,0], [0,-1], [0,1]]
for d in ds:
r_, c_ = r + d[0], c + d[1]
if not valid(r_, c_):
continue
if flow_map[r_][c_] == 1:
continue
if heights[r_][c_] >= heights[r][c]:
flow_map[r_][c_] = 1
flow_map = reverse_flow(r_, c_, flow_map)
return flow_map
for i in range(n):
po_map = reverse_flow(0, i, po_map)
ao_map = reverse_flow(m-1,i, ao_map)
for i in range(m):
po_map = reverse_flow(i, 0, po_map)
ao_map = reverse_flow(i, n-1, ao_map)
# merge two map
res = []
for r in range(m):
for c in range(n):
if po_map[r][c] == 1 and ao_map[r][c] == 1:
res.append([r,c])
return res
200. Number of Islands
Given an m x n 2D binary grid grid which represents a map of ‘1’s (land) and ‘0’s (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1
- Use visited to track the visited cells.
- Use DFS to explore the grid. if the cell is not visited and the cell is “1” and not connected to other islands, then it is a new island.
def numIslands(self, grid: List[List[str]]) -> int:
m = len(grid)
n = len(grid[0])
visited = [[0 for _ in range(n)] for _ in range(m)]
def valid(r, c):
if r < 0 or r >= m:
return False
if c < 0 or c >= n:
return False
return True
def dfs(r,c,ni):
# directions [up, down, left, right]
ds = [[-1,0], [1,0], [0,-1], [0,1]]
if grid[r][c] == "0":
return 0
if visited[r][c] == 1:
return 0
visited[r][c] = 1
ni += 1
for d in ds:
r_, c_ = r + d[0], c + d[1]
if not valid(r_, c_):
continue
if grid[r_][c_] == "0":
continue
if visited[r_][c_] == 1:
continue
# grid[r_][c_] == "1" and not visited
# print(r, c, r_, c_, ni, visited)
ni = dfs(r_, c_, ni)
return ni
num_islands = 0
for r in range(m):
for c in range(n):
num_islands += 1 if dfs(r,c,0) > 0 else 0
return num_islands
212. Word Search II
Given an m x n board of characters board and a list of strings words, return all words on the board.
Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example 1:
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
m, n = len(board), len(board[0])
used = [[False for _ in range(n)] for _ in range(m)]
def findWord(board, word):
# backtrack
def backtrack(row, col, i):
# boundary
if row < 0 or row > m - 1 or col < 0 or col > n - 1:
return False
if i == len(word) - 1:
# last letter
return board[row][col] == word[i] if not used[row][col] else False
if board[row][col] == word[i] and not used[row][col]:
used[row][col] = True
a = backtrack(row-1, col, i+1)
b = backtrack(row+1, col, i+1)
c = backtrack(row, col-1, i+1)
d = backtrack(row, col+1, i+1)
used[row][col] = False
return any([a, b, c, d])
else:
return False
# search first word
is_found = [False]
for row in range(m):
for col in range(n):
if board[row][col] == word[0]:
is_found.append(backtrack(row, col, 0))
return any(is_found)
output = [word for word in words if findWord(board, word)]
return output
The backtracking solution is not efficient because it is not pruning the invalid paths. We can use Trie to improve the efficiency. The idea is to build a Trie from the words and then use the Trie to search the board.
Strategy to search the board:
- Scan the board and for each cell, backtrack from the root of the Trie, i.e., backtrack(row, col, root)
- If the current character is in node.children, we set the node to the current character, and search in four directions for the next character.
class TrieNode:
def __init__(self):
self.children = dict()
self.word = None # to store the word if it is the last letter
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
node = self.root
for l in word:
if l not in node.children:
# add l as a node.children
node.children[l] = TrieNode()
node = node.children[l]
node.word = word # last letter
def search(self, word):
node = self.root
for l in word:
if l not in node.children:
return False
node = node.children[l]
return True
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
m, n = len(board), len(board[0])
result = []
trie = Trie()
for word in words:
trie.insert(word)
def backtrack(row, col, node):
# boundary
if row < 0 or col < 0 or row >= m or col >= n:
return
# reach the last character
if node.word is not None:
result.append(node.word)
node.word = None # delete to avoid duplicate
if board[row][col] in node.children:
# mark visited
c = board[row][col]
board[row][col] = '#'
backtrack(row-1, col, node.children[c])
backtrack(row+1, col, node.children[c])
backtrack(row, col-1, node.children[c])
backtrack(row, col+1, node.children[c])
board[row][col] = c
for row in range(m):
for col in range(n):
backtrack(row, col, trie.root)
return result
73. Set Matrix Zeroes
Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0’s.
You must do it in place.
Example 1:
Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]
Key idea is to use the first row and first column as the marker to indicate if the row or column should be set to 0. However, we need to be careful when the first row itself contains a 0.
- To handle this case, we need a flag
rowZEROto indicate if the first row itself contains a 0. - We iterate columns from right to left to avoid overwriting the marker.
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
ROWS = len(matrix)
COLS = len(matrix[0])
rowZERO = False
for r in range(ROWS):
for c in range(COLS):
if matrix[r][c] == 0:
if r > 0:
matrix[0][c] = 0
matrix[r][0] = 0
else:
rowZERO = True
matrix[0][c] = 0
for r in range(1,ROWS):
for c in range(COLS-1,-1,-1):
if matrix[0][c] == 0:
matrix[r][c] = 0
if matrix[r][0] == 0:
matrix[r][c] = 0
if rowZERO:
for c in range(COLS):
matrix[0][c] = 0
54. Spiral Matrix
Given an m x n matrix, return all elements of the matrix in spiral order.
Example 1:
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
def move_right(r, c):
return r, c+1
def move_left(r, c):
return r, c-1
def move_up(r, c):
return r-1, c
def move_down(r, c):
return r+1, c
def move(r, c, direction):
if direction == 'move_right':
return move_right(r, c)
elif direction == 'move_down':
return move_down(r, c)
elif direction == 'move_up':
return move_up(r, c)
elif direction == 'move_left':
return move_left(r, c)
else:
raise ValueError
def valid(r, c, left_col, right_col, top_row, bot_row):
if r < top_row or r > bot_row:
return False
if c < left_col or c > right_col:
return False
return True
def change_direction(direction, left_col, right_col, top_row, bot_row):
if direction == 'move_right':
return 'move_down', left_col, right_col, top_row + 1, bot_row
elif direction == 'move_down':
return 'move_left', left_col, right_col - 1, top_row, bot_row
elif direction == 'move_left':
return 'move_up', left_col, right_col, top_row, bot_row - 1
elif direction == 'move_up':
return 'move_right', left_col + 1, right_col, top_row, bot_row
else:
raise ValueError
def next_move(r, c, direction, left_col, right_col, top_row, bot_row):
temp_r, temp_c = move(r, c, direction)
if valid(temp_r, temp_c, left_col, right_col, top_row, bot_row):
return direction, left_col, right_col, top_row, bot_row
else:
return change_direction(direction, left_col, right_col, top_row, bot_row)
output = []
direction = 'move_right'
r, c = 0, 0
ROWS = len(matrix)
COLS = len(matrix[0])
left_col = 0
right_col = COLS - 1
top_row = 0
bot_row = ROWS - 1
while len(output) < ROWS * COLS:
output.append(matrix[r][c])
direction, left_col, right_col, top_row, bot_row = next_move(r, c, direction, left_col, right_col, top_row, bot_row)
r, c = move(r, c, direction)
return output
392. Is Subsequence
Given two strings s and t, return true if s is a subsequence of t, or false otherwise.
A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
def helper(s, t):
if len(s) == 0:
return True
if len(t) == 0:
return False
if s[0] == t[0]:
return helper(s[1:], t[1:])
else:
return helper(s, t[1:])
return helper(s, t)
338. Counting Bits
Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] is the number of 1’s in the binary representation of i.
- The largest number of 1’s can be at most
log2(n) + 1. - When adding
0to the end of the number, the value of the number is doubled, but the number of 1’s is the same. i.e.,1010= 2 *101. dp[i] = dp[i/2]. if i is even - When adding
1to the end of the number, the number of 1’s is the number of 1’s in the previous number plus 1. i.e.,1011= 2 *101+ 1. dp[i] = dp[(i-1)/2] + 1. if i is odd
class Solution:
def countBits(self, n: int) -> List[int]:
dp = [0] * (n+1)
dp[0] = 0
for i in range(1, n+1):
if i % 2 == 0:
dp[i] = dp[i//2]
else:
dp[i] = dp[(i-1)//2] + 1
return dp
746. Min Cost Climbing Stairs
You are given an integer array cost where cost[i] is the cost of the i-th step on a staircase. Once you pay the cost, you can either climb one or two steps.
You can either start from the step with index 0, or the step with index 1.
Return the minimum cost to reach the top of the floor.
Example 1:
Input: cost = [10,15,20]
Output: 15
It is because there only three steps [start, 10, 15, 20, top], and we can climb one or two steps at a time. Therefore, the best way is from start -> 15 -> top.
SolutionObservation:
- [start] + cost + [top]: add two dummy nodes at the beginning and end of the array.
- dp[top] = 0
- dp[top-1] = cost[-1]
- dp[top-2] = cost[-2]
- dp[top-3] = min(dp[top-1] + cost[top-3], dp[top-2] + cost[top-2]). It is because we can either climb one or two steps at a time. So from the current step, we will climb to the one that is cheaper.
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
dp = [0] * (n+1)
cost = cost + [0]
dp[n] = cost[n] # 0
dp[n-1] = cost[n-1] #
for i in range(n-2,-1,-1):
dp[i] = min(cost[i] + dp[i+1], cost[i] + dp[i+2])
return min(dp[0], dp[1])
191. Number of 1 Bits
Write a function that takes an unsigned integer and returns the number of 1’s bits it has (also known as the Hamming weight).
Example 1:
Input: n = 11 (00000000000000000000000000001011)
Output: 3
class Solution:
def hammingWeight(self, n: int) -> int:
count = 0
while n:
if n % 2 == 1:
count += 1
n = n // 2
return count
268. Missing Number
Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
Example 1:
Input: nums = [3,0,1]
Output: 2
class Solution:
def missingNumber(self, nums: List[int]) -> int:
return sum(range(len(nums)+1)) - sum(nums)
1143. Longest Common Subsequence
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
For example, “ace” is a subsequence of “abcde”.
Example 1:
Input: text1 = "abcde", text2 = "ace"
Output: 3
Observation:
- We need a 2D dp array to store the longest common subsequence. dp[]
- if text1[i] == text2[j], then dp[i][j] = dp[i-1][j-1] + 1
- if text1[i] != text2[j], then dp[i][j] = max(dp[i-1][j], dp[i][j-1])
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
l1 = len(text1) # num columns
l2 = len(text2) # num rows
dp = [[0 for _ in range(l1+1)] for _ in range(l2+1)]
for i2 in range(1, l2+1):
for i1 in range(1, l1+1):
i1m1 = i1 - 1
i2m1 = i2 - 1
if text1[i1m1] == text2[i2m1]:
dp[i2][i1] = dp[i2m1][i1m1] + 1
else:
dp[i2][i1] = max(dp[i2m1][i1], dp[i2][i1m1])
return dp[-1][-1]
91. Decode Ways
You have intercepted a secret message encoded as a string of numbers. The message is encoded using the following mapping:
'1' -> 'A'
'2' -> 'B'
...
'26' -> 'Z'
However, while decoding the message, you realize that there are many different ways you can decode the message because some codes are contained in other codes (“2” and “5” vs “25”).
For example, the message “11106” can be decoded as “AAJF” with the grouping (1 1 10 6) or “KJF” with the grouping (11 10 6).
Note: there may be strings that are impossible to decode.
Given a string s containing only digits, return the number of ways to decode it. If the entire string cannot be decoded in any valid way, return 0.
Example 1:
Input: s = "12"
Output: 2
Example 2:
Input: s = "226"
Output: 3
class Solution:
def numDecodings(self, s: str) -> int:
dp = [0] * (len(s)+1)
dp[0] = 1
dp[1] = 1 if s[0] != '0' else 0
for i in range(2, len(s)+1):
if s[i-1] != '0':
dp[i] = dp[i-1]
if 10 <= int(s[i-2:i]) <= 26:
dp[i] += dp[i-2]
return dp[-1]
39. Combination Sum
Given a set of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
The same number may be chosen from candidates an unlimited number of times.
Example 1:
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Observations:
- Backtracking:
- dp[7] = [2 + dp[5] if dp[5] is valid, 3 + dp[4] if dp[4] is valid, 6 + dp[1] if dp[1] is valid, 7 + dp[0] if dp[0] is valid]
- Similarly, dp[5] = [2 + dp[3] if dp[3] is valid, 3 + dp[2] if dp[2] is valid, 6 + dp[-1] if dp[-1] is valid, 7 + dp[-2] if dp[-2] is valid]
- All dp[i] with i < 0 are invalid.
- We can build a tree to visualize the process. With the root being the current number t, and children being t - candidates[i]. valid children are the ones that are >= 0.
- How to form the results?
- We can use a list to store the current path, i.e., dp[0] = [], dp[1] = [], dp[2] = [[2]], dp[3] = [[3]], dp[4] = [[2, 2]] = [dp[2] + [2]], dp[5] = [[2, 3]] = [dp[3] + [2]], dp[6] = [dp[3] + [3], dp[4] + [2]], etc.
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
dp = [[]] * (target + 1)
dp[0] = [] # format of each dp[i]
for t in range(1, target+1):
for c in candidates:
print(t, c, dp)
if t - c < 0:
continue
elif t - c == 0:
# add [c] to the current list
if dp[t] == []:
dp[t] = [[c]]
else:
dp[t].append([c])
else:
if dp[t-c] == []:
# empty []
continue
else:
# add c to the current list
# e.g., dp[2] before [], after [[2]]
# e.g., dp[4] before [], after adding dp[2], [[2, 2]]
# e.g., dp[6] before [], after adding dp[3]=[[3]] is [[3, 3]], after adding dp[4]=[[2,2]] is [[3,3], [2,2,2]]
assert len(dp[t-c]) >= 1, dp[t-c]
assert len(dp[t-c][0]) >= 1, dp[t-c]
assert type(dp[t-c][0]) is list, dp[t-c]
assert type(dp[t-c][0][0]) is int, dp[t-c]
new = [l + [c] for l in dp[t-c]]
if dp[t] == []:
dp[t] = new
else:
dp[t].extend(new)
assert type(dp[t]) is list, dp[t]
assert type(dp[t][0]) is list, dp[t]
assert type(dp[t][0][0]) is int, dp[t]
return dp[target]
The above solution does not work because it does not consider the duplicate solutions like [2,2,3] and [2,3,2]. To address this issue, we need to sort the candidates and only add a number to the current list if it is greater than the last number in the current list.
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort() # Sorting helps maintain order
dp = [[] for _ in range(target + 1)]
dp[0] = [[]] # Base case: one way to sum to 0 (empty set)
for c in candidates: # Iterate candidates first
for t in range(c, target + 1): # Build up DP array
for comb in dp[t - c]:
if not comb or c >= comb[-1]: # Ensure non-decreasing order
dp[t].append(comb + [c]) # Append new valid combination
return dp[target]
The backtracking solution is as follows:
def combinationSum(candidates, target):
result = []
def backtrack(start, path, remaining):
# Base cases
if remaining == 0: # Found a valid combination
result.append(list(path)) # Create a new list to avoid reference issues
return
if remaining < 0: # Invalid path, sum exceeded target
return
# Try each candidate from the current starting position
for i in range(start, len(candidates)):
# Make choice
path.append(candidates[i])
# Explore further with this choice
# Keep start as i to allow reusing the same number
backtrack(i, path, remaining - candidates[i])
# Undo choice (backtrack) to try next candidate
path.pop()
backtrack(0, [], target)
return result
Let’s visualize how this works with candidates = [2,3,6,7] and target = 7:
7
/ | | \
2(5) 3(4) 6(1) 7(0)✓
/ | \ | \ |
2(3) 3(2) 6(-) 3(1) 6(-) 6(-)
/ | | |
2(1) 3(0)✓ 6(-) 3(-)
/
2(-)
Numbers in parentheses show remaining value after each choice
✓ indicates a valid combination found
- indicates an invalid path (remaining < 0)
Key points about this solution:
-
The
startparameter ensures we don’t use numbers before the current position, preventing duplicates like [2,3] and [3,2] -
We can reuse numbers by passing
iinstead ofi+1in the recursive call -
The
pathlist tracks our current combination being built -
The
remainingparameter helps us track how much more we need to sum to reach target
This approach has several advantages:
- Memory efficient as it only stores valid combinations
- Naturally avoids duplicates by maintaining order
- Can handle unlimited reuse of numbers
90. Subsets II
Given a collection of integers that might contain duplicates, return all possible subsets (the power set).
Example 1:
Input: [1,2,2]
Output:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
Observations:
- The subsets can be found by removing one element at a time from the original list and find the subsets of the remaining list.
- It is a backtracking problem.
- We can use a set to store the subsets to avoid duplicates. For example, [1,2] and [2,1] are the same.
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
results = []
nums.sort()
def backtrack(start, path):
results.append(path[:])
for i in range(start, len(nums)):
if i > start and nums[i] == nums[i-1]:
continue
path.append(nums[i])
backtrack(i + 1, path)
path.pop()
backtrack(0, [])
return results
Very important point:
-
pathis a mutable object (list) that gets modified throughout the recursion -
path[:]creates a new copy of the list at that point in time - When you use
results.append(path), all entries inresultspoint to the same list object - When you backtrack and modify
path, it changes all previous references to that list
Therefore:
-
results.append(path)- all sublists inresultswill end up being the same (empty after all backtracking is done) -
results.append(path[:])- each sublist is an independent copy representing the state ofpathat that moment
This is why path[:] (or path.copy() or list(path)) is necessary for backtracking problems where you need to store the intermediate states of your path.
46. Permutations
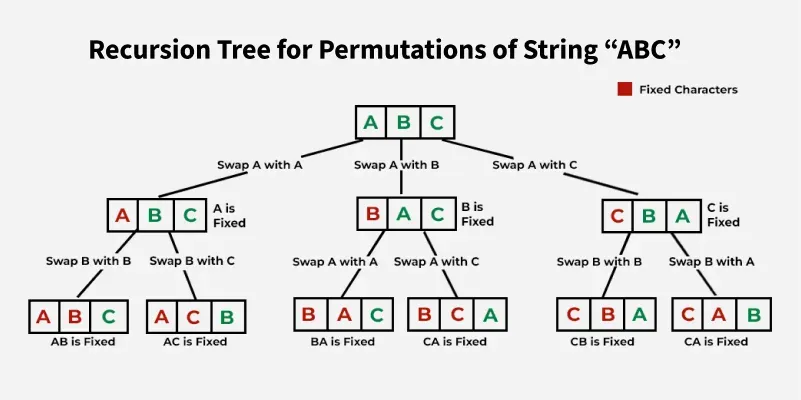
Given a collection of distinct integers, return all possible permutations.
Example 1:
Input: [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Observations:
- A permutation can be found by adding one number at a time until the length of the permutation is equal to the length of the original list.
- We need
usedto track the numbers that have been used. - The greedy approach is O(N^N) because we need to try all possible combinations.
- The backtracking approach is O(N!)
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
results = []
nums.sort()
used = [False] * len(nums)
def backtrack(path):
if len(path) == len(nums):
results.append(list(path))
return
for i in range(len(nums)):
if used[i]:
continue
if i > 0 and nums[i] == nums[i-1] and not used[i-1]:
continue
used[i] = True
path.append(nums[i])
backtrack(path)
path.pop()
used[i] = False
backtrack([])
return results
257. Binary Tree Paths
Given a binary tree, return all root-to-leaf paths.
Example 1:
Input:
1
/ \
2 3
\
5
Output: ["1->2->5", "1->3"]
Observations:
- A path can be found by adding one node at a time until the node is a leaf node.
- Need to check if the node is a leaf node.
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
result = []
def dfs(node, path):
if not node:
return
path.append(node.val)
if node.left is None and node.right is None:
# leaf node
result.append("->".join(map(str, path)))
else:
if node.left is not None:
dfs(node.left, path)
if node.right is not None:
dfs(node.right, path)
path.pop()
dfs(root, [])
return result
51. N-Queens
Reference from Geeksforgeeks: https://www.geeksforgeeks.org/n-queen-problem-backtracking-3/
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Observations:
- A queen can be placed in a row, column, or diagonal.
- We need to check if the queen is in the same row, column, or diagonal as any other queen.
- Same row:
row[i] == row[j] - Same column:
col[i] == col[j] - left diagonal:
row[i] + col[i] == row[j] + col[j] - right diagonal:
row[i] - col[i] == row[j] - col[j]
- Same row:
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
results = []
CELL_EMPTY = '.'
CELL_QUEEN = 'Q'
CELL_NA = 'NA'
board = [[CELL_EMPTY for _ in range(n)] for _ in range(n)]
def convert_array_to_string_board(board):
# remove the NA cells
return ["".join(row).replace(CELL_NA, CELL_EMPTY) for row in board]
def fill_board_with_a_queen(board, row, col):
# Given a board and a position (row, col), fill the board with a queen - row, col, left diagonal, right diagonal
assert len(board) == n
assert len(board[0]) == n
board[row][col] = CELL_QUEEN
for i in range(n):
board[i][col] = CELL_NA
board[row][i] = CELL_NA
row_plus_i = min(row + i, n - 1)
row_minus_i = max(row - i, 0)
col_plus_i = min(col + i, n - 1)
col_minus_i = max(col - i, 0)
# left diagonal, [row_minus_i, col_plus_i] and [row_plus_i, col_minus_i]
board[row_minus_i][col_plus_i] = CELL_NA
board[row_plus_i][col_minus_i] = CELL_NA
# right diagonal, [row_minus_i, col_minus_i] and [row_plus_i, col_plus_i]
board[row_minus_i][col_minus_i] = CELL_NA
board[row_plus_i][col_plus_i] = CELL_NA
return board
def remove_queen_from_board(board, row, col):
board[row][col] = CELL_EMPTY
for i in range(n):
board[i][col] = CELL_EMPTY
board[row][i] = CELL_EMPTY
row_plus_i = min(row + i, n - 1)
row_minus_i = max(row - i, 0)
col_plus_i = min(col + i, n - 1)
col_minus_i = max(col - i, 0)
# left diagonal, [row_minus_i, col_plus_i] and [row_plus_i, col_minus_i]
board[row_minus_i][col_plus_i] = CELL_EMPTY
board[row_plus_i][col_minus_i] = CELL_EMPTY
# right diagonal, [row_minus_i, col_minus_i] and [row_plus_i, col_plus_i]
board[row_minus_i][col_minus_i] = CELL_EMPTY
board[row_plus_i][col_plus_i] = CELL_EMPTY
return board
def is_valid_position(board, row, col):
# check if the position is valid
return board[row][col] == CELL_EMPTY
def backtrack(board, prev_rows, prev_cols):
if len(prev_rows) == n:
results.append(convert_array_to_string_board(board))
return
for col in range(n):
if col in prev_cols:
continue
for row in range(n):
if row in prev_rows:
continue
if not is_valid_position(board, row, col):
continue
prev_rows.append(row)
prev_cols.append(col)
fill_board_with_a_queen(board, row, col)
backtrack(board, prev_rows, prev_cols)
remove_queen_from_board(board, row, col)
prev_rows.pop()
prev_cols.pop()
backtrack(board, [], [])
return results
Turn out the above solution is not correct. The board has been modified in the process of backtracking.
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
results = []
board = [["."] * n for _ in range(n)]
cols = set()
pos_diagonals = set()
neg_diagonals = set()
def backtrack(row):
if row == n:
results.append(["".join(row) for row in board])
return
for col in range(n):
if col in cols or (row + col) in pos_diagonals or (row - col) in neg_diagonals:
continue
cols.add(col)
pos_diagonals.add(row + col)
neg_diagonals.add(row - col)
board[row][col] = 'Q'
backtrack(row + 1)
# remove the queen
cols.remove(col)
pos_diagonals.remove(row + col)
neg_diagonals.remove(row - col)
board[row][col] = '.'
backtrack(0)
return results
17. Letter Combinations of a Phone Number
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
Example 1:
Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if len(digits) == 0:
return []
map_letter = {
'2': ['a', 'b', 'c'],
'3': ['d', 'e', 'f'],
'4': ['g', 'h', 'i'],
'5': ['j', 'k', 'l'],
'6': ['m', 'n', 'o'],
'7': ['p', 'q', 'r', 's'],
'8': ['t', 'u', 'v'],
'9': ['w', 'x', 'y', 'z']
}
results = []
def backtrack(start, path):
if len(path) == len(digits):
results.append("".join(path))
return
for i in range(start, len(digits)):
d = digits[i]
for j in range(len(map_letter[d])):
path.append(map_letter[d][j])
backtrack(i+1, path)
path.pop()
backtrack(0, [])
return results
77. Combinations
Given two integers n and k, return all possible combinations of k numbers out of the range [1, n].
You may return the answer in any order.
Example 1:
Input: n = 4, k = 2
Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
results = []
used = [False] * (n+1)
def backtrack(start, path):
if len(path) == k:
results.append(list(path))
return
for i in range(start, n+1):
if used[i]:
continue
used[i] = True
path.append(i)
backtrack(i, path)
path.pop()
used[i] = False
backtrack(1, [])
return results
22. Generate Parentheses
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
Example 1:
Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]
Observations:
- The number of left parentheses must be equal to the number of right parentheses.
- We can count the number of open and close parentheses. If close > open means invalid path
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
results = []
data = ['('] * n + [')'] * n
used = [False] * 2 * n
def count_open(path):
count = 0
for s in path:
if s == '(':
count += 1
return count
def count_close(path):
count = 0
for s in path:
if s == ')':
count += 1
return count
def backtrack(path):
if len(path) == 2*n and count_open(path) == count_close(path):
t = "".join(path)
if t not in results:
results.append(t)
return
if count_open(path) < count_close(path):
# invalid
return
for i in range(2*n):
if used[i]:
continue
used[i] = True
path.append(data[i])
backtrack(path)
path.pop()
used[i] = False
backtrack([])
return results
The above solution is not optimal.
- Checking validity using
count_openandcount_closeis not efficient. We can use two counters to track the number of open and close parentheses.
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
results = []
def backtrack(path, openP, closeP):
if openP == closeP == n:
results.append("".join(path))
return
if openP < n:
path.append("(")
backtrack(path, openP+1, closeP)
path.pop()
if closeP < openP:
path.append(")")
backtrack(path, openP, closeP+1)
path.pop()
backtrack([], 0, 0)
return results
79. Word Search
Given a m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Observations:
- We can use backtracking to solve this problem.
- We need to scan the board to find the first character of the word.
- If found, we can mark the cell as visited and
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
m, n = len(board), len(board[0])
def backtrack(row, col, idx):
if idx == len(word):
return True # Found the word
if row < 0 or row >= m or col < 0 or col >= n: # Out of bounds
return False
if board[row][col] != word[idx]: # Mismatch
return False
temp = board[row][col] # Mark as visited
board[row][col] = "#"
# Explore all 4 directions
found = (backtrack(row + 1, col, idx + 1) or
backtrack(row - 1, col, idx + 1) or
backtrack(row, col + 1, idx + 1) or
backtrack(row, col - 1, idx + 1))
board[row][col] = temp # Restore the cell
return found
# Start backtracking from any matching cell
for i in range(m):
for j in range(n):
if board[i][j] == word[0] and backtrack(i, j, 0):
return True
return False
120. Triangle
Given a triangle array, return the minimum path sum from top to bottom.
For each step, you may move to an adjacent number of the row below. More formally, if you are on index i on the current row, you may move to either index i or index i + 1 on the next row.
Example 1:
Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
Output: 11
Backtrack solution:
- Return case: when the row is the last row.
- Recursive case: for each [row][col], we can move to [row+1][col] or [row+1][col+1].
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
min_path_sum = float("inf")
def backtrack(row, col, path_sum):
nonlocal min_path_sum
path_sum += triangle[row][col]
if row == n - 1:
min_path_sum = min(min_path_sum, path_sum)
return
backtrack(row+1, col, path_sum)
backtrack(row+1, col+1, path_sum)
backtrack(0,0,0)
return min_path_sum
However, the backtrack solution is not efficient because it explores all possible paths, including paths that have been computed. Complexity is O(2^n).
Dynamic programming solution:
- Use a 2D array to store the minimum path sum for each cell.
- The value of each cell is the sum of the value of the cell and the minimum of the values of the two cells directly below it.
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
dp = [[float("inf") for _ in range(n)] for _ in range(n)]
dp[0][0] = triangle[0][0]
for row in range(1, n):
for col in range(len(triangle[row])):
if col == 0:
dp[row][col] = dp[row-1][col] + triangle[row][col]
else:
dp[row][col] = min(dp[row-1][col], dp[row-1][col-1]) + triangle[row][col]
return min(dp[-1])
64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
Example 1:
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
dp = [[float("inf") for _ in range(n)] for _ in range(m)]
for row in range(m):
for col in range(n):
if row == 0 and col == 0:
dp[row][col] = grid[0][0]
elif row == 0:
dp[row][col] = dp[row][col-1] + grid[row][col]
elif col == 0:
dp[row][col] = dp[row-1][col] + grid[row][col]
else:
dp[row][col] = min(dp[row][col-1], dp[row-1][col]) + grid[row][col]
return dp[-1][-1]
63. Unique Paths II
You are given an m x n integer array obstacleGrid. An obstacle and space are marked as 1 or 0 respectively in the grid.
A path that the robot takes cannot include any square that is an obstacle.
Return the number of unique paths that the robot can take to reach the bottom-right corner.
Example 1:
Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [[0 for _ in range(n)] for _ in range(m)]
for row in range(m):
for col in range(n):
if row == 0 and col == 0:
dp[row][col] = 1 if obstacleGrid[row][col] == 0 else 0
elif row == 0:
dp[row][col] = dp[row][col-1] if obstacleGrid[row][col-1] == 0 else 0 # else 0
elif col == 0:
dp[row][col] = dp[row-1][col] if obstacleGrid[row-1][col] == 0 else 0 # else 0
else:
dp[row][col] = dp[row][col-1] * (1 - obstacleGrid[row][col-1]) + dp[row-1][col] * (1 - obstacleGrid[row-1][col])
return dp[-1][-1] if obstacleGrid[-1][-1] == 0 else 0
5. Longest Palindromic Substring
Given a string s, return the longest palindromic substring in s.
Example 1:
Input: s = "babad"
Output: "bab"
Observations:
- We can use DP 2D to solve this problem.
- dp[i][i] = True because a single character is a palindrome.
- dp[i][j] = True if dp[i+1][j-1] = True and s[i] == s[j]
- max_length = max(max_length, j-i+1)
- start = i that has the max_length. We need max_length and start to return the result.
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
dp = [[False for _ in range(n)] for _ in range(n)]
start = 0
max_length = 0
if len(s) == 1:
return s
for i in range(n):
dp[i][i] = True
start = i
max_length = 1
for length in range(2, n+1):
for l in range(0, n - length + 1):
r = l + length - 1
if s[l] == s[r]:
if length == 2 or dp[l+1][r-1]:
dp[l][r] = True
if length > max_length:
max_length = length
start = l
return s[start:start+max_length]
Reflection
Backtracking
Backtracking is a recursive algorithm used for solving problems that require exploring all possible solutions and pruning incorrect paths. It is particularly useful for combinatorial problems such as Combination Sum, or finding all possible path from root to leaf in a tree.
- Technique: Recursive exploration with pruning.
- Complexity: O(2ⁿ) for subsets, O(N!) for permutations
If a problem involves:
- Generating all possible solutions → Use backtracking
- Making choices with constraints → Use backtracking
- Exploring all paths in a grid, tree, or graph → Use backtracking
Key Concept:
- Make a choice
- Recur with that choice
- Undo the choice (backtrack)
- In some cases, we need to sort the input array first.
- In some cases, we need to use a
usedarray to track the used elements, e.g., 77. Combinations
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
nums.sort()
def backtracking(start, path):
result.append(list(path))
for i in range(start, len(nums)):
if i > start and nums[i] == nums[i-1]:
continue
path.append(nums[i])
backtracking(i+1, path)
path.pop()
backtracking(0, [])
return result
def FIND_SOLUTIONS(parameters):
if (valid_solution):
store_the_solution()
return
for choice in all_choices:
if valid_choice(choice):
APPLY(choice)
FIND_SOLUTIONS(parameters)
BACKTRACK(remove_choice)
Two-pointer
In-place operations
In-place operations modify the array without using extra space for another data structure. This is useful for optimizing space complexity. However, in-place operations require careful handling to avoid overwriting important data.
Key Advantages of In-Place Operations:
- Saves Space → Avoids creating extra arrays, reducing memory usage from O(n) to O(1).
- Efficient in Practice → Less memory access and allocation make the program faster.
- Useful for Large Datasets → Ideal for problems with constraints on space.
Combine with Two-pointer:
left, right = 0, len(nums) - 1
while left < right:
# do something
s[left], s[right] = s[right], s[left]
# update left and right
left += 1
right -= 1
Enjoy Reading This Article?
Here are some more articles you might like to read next: