Lesson Learned from NeurIPS 2023 Machine Unlearning Challenge
About the challenge
- Challenge page: https://www.kaggle.com/competitions/neurips-2023-machine-unlearning/overview, https://unlearning-challenge.github.io/
- Motivation of machine unlearning:
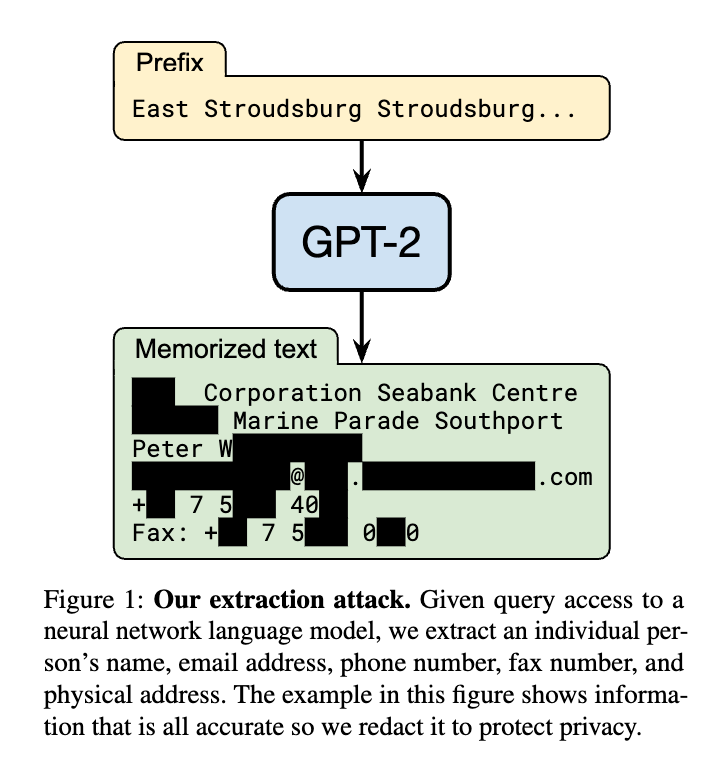
- Large models tend to memorize details of their training set and can be exploited to recover private information about individuals, i.e., by using membership inference attacks (Shokri et al., 2017) or model inversion attacks (Fredrikson et al., 2015).
- \(\rightarrow\) Privacy concerns arise when big tech companies collect and store large amounts of data about individuals (e.g., face images, voice recordings, search history, etc.) and train machine learning models on this data then release these models to the public, for example, StabilityAI’s Stable Diffusion models, Google’s Gemma, etc.
- \(\rightarrow\) Goverments and organizations (e.g., the European Union) have introduced regulations to protect individuals’ privacy rights (e.g., individuals have the “right to be forgotten” under the EU’s General Data Protection Regulation (Mantelero, 2013) or Canada’s Personal Information Protection and Electronic Documents Act)
- \(\rightarrow\) Machine learning developers like Google, OpenAI must ensure their models meet these requirements, i.e., they must be able to “unlearn” certain data from their models to comply with these regulations. These removal requests can be made by individuals or organizations and can be made at any time after the model has been trained and deployed.
- \(\rightarrow\) Retraining the model from scratch is very expensive and sometimes infeasible due to the entanglement of the data in the vast training set, for example, finding all Harry Potter references in a trillion tokens.
\(\rightarrow\) The need for machine unlearning algorithms that can remove specific data from a model without significantly affecting its performance on the remaining data


Task and Data
The challenge centers on the scenario in which an age predictor is built from face image data and, after training, a certain number of images must be forgotten to protect the privacy or rights of the individuals concerned.

Some teminologies/settings in the challenge (More details can be found in the challenge whitepaper)
- Original Model: A pre-trained model that predicts the age of a person from a face image. This is a discriminator/classifier model that takes an image as input and outputs a probability distribution over age classes.
- Train set \(D\): A set of face images with associated age labels used to train the model.
- Forget set \(S \subseteq D\): A set of face images with associated age labels that must be forgotten.
- Retain set: The set of face images with associated age labels that must be retained. This is the train set exclude the forget set \(D \ S\).
- Secret Model: The model that is trained on the retain set only. This is the model that the unlearning algorithm must produce/match.
- Goal: The unlearning algorithm must produce a model that is indistinguishable from the model trained without the forget set.
Define Machine Unlearning
For a fixed dataset \(D\), forget set \(S \subseteq D\), and a randomized learning algorithm \(A\), an unlearning algorithm \(U\) is \((\epsilon, \delta)\)-unlearning with respect to \((D, S, A)\) if for all regions \(R \subseteq \mathcal{R}\), we have that
\[Pr[A(D \setminus S) \in R] \leq e^{\epsilon} Pr[U(A(D),S,D) \in R] + \delta\]and
\[Pr[U(A(D),S,D) \in R] \leq e^{\epsilon} Pr[A(D \setminus S) \in R] + \delta\]where \(\mathcal{R}\) is the output space of the learning algorithm \(A\), for example, if using a neural network, \(\mathcal{R}\) is the space of all possible weight configurations of the network, and \(R\) is a region in this space.
\(A(D), A(D \setminus S)\) are the outputs of the learning algorithm \(A\) on the datasets \(D\) and \(D \setminus S\) (the “retain set”), respectively. \(U(A(D), S, D)\) is the output of the unlearning algorithm \(U\) on the model trained on \(D\), given access to the forget set \(S\) and the train set \(D\).
Intuitively, when \(\epsilon\) and \(\delta\) are small (i.e., \(e^{\epsilon} \approx 1 + \epsilon\) and \(\delta \approx 0\)), the unlearning algorithm \(U\) is indistinguishable from the learning algorithm \(A\) when the forget set \(S\) is removed from the train set \(D\).
Side note: The above definition is a bit different from the standard definition of differential privacy (DP). Please refer to the challenge whitepaper for more details.
Define the Evaluation Metric
The advantage of the above definition is that it is agnostic the output space of the learning algorithm \(A\) while not specifying the type of learning algorithm. This allows the definition to be applied to a wide range of learning algorithms, including discriminative models, generative models. However, this also makes it difficult to define a specific evaluation metric for the unlearning algorithm. For example, in the case of neural network, it is nearly impossible to compare the weights of the neural network before and after unlearning directly. In Differential Privacy literature, to evaluate the effectiveness of a DP algorithm, we make use of a membership inference attack, which can inspect the model output and determine whether a specific sample (i.e., \(S\)) was used in the training set or not. As defined above, the DP’s performance can be quantified by the \(\epsilon\) and \(\delta\) parameters, i.e., the smaller the \(\epsilon\) and \(\delta\), the better the DP algorithm.
DP can be interpreted as a hypothesis test with the null hypothesis that \(A\) was trained on \(D\) and the alternative hypothesis that A was trained on \(D \setminus S\). False positives (type-I errors) occur when the null hypothesis is true, but is rejected, while false negatives (type-II errors) occur when the alternative hypothesis is true, but is rejected. In Kairouz et al. (2015), the authors proposed an estimation of \(\epsilon\) at a fixed \(\delta\) as follows:
\[\hat{\epsilon} = \max \left\{ \log \frac{1 - \delta - \hat{\text{FPR}}}{\hat{\text{FNR}}}, \log \frac{1 - \delta - \hat{\text{FNR}}}{\hat{\text{FPR}}} \right\}\]where \(\hat{\text{FPR}}\) and \(\hat{\text{FNR}}\) are the false positive rate and false negative rate of the membership inference attack, respectively. The FPR and FNR can be estimated by
The final evaluation metric as follow:
\[\mathcal{F}(\hat{\epsilon}) \times \frac{\text{RA}^{U}}{\text{RA}^{R}} \times \frac{\text{TA}^{U}}{\text{TA}^{R}}\]where \(\mathcal{F}(\hat{\epsilon})\) is a function of \(\hat{\epsilon}\) that rewards small values of \(\hat{\epsilon}\), \(\text{RA}, \text{TA}\) are the accuracy of the model on the retain set and holdout test set, respectively. The superscripts \(U, R\) denote the model produced by the unlearning algorithm and the secret model trained on the retain set, respectively. Intuitively, the above formula adjusts the forgetting quality F based on utility, by penalizing an unlearning algorithm if either its retain or test (average) accuracy is smaller than the corresponding average accuracy of retraining.
Winning solutions
to be updated
References
Enjoy Reading This Article?
Here are some more articles you might like to read next: