Less is More - Recursive Reasoning with Tiny Networks
About the paper
Implementation
Data preparation
Main process
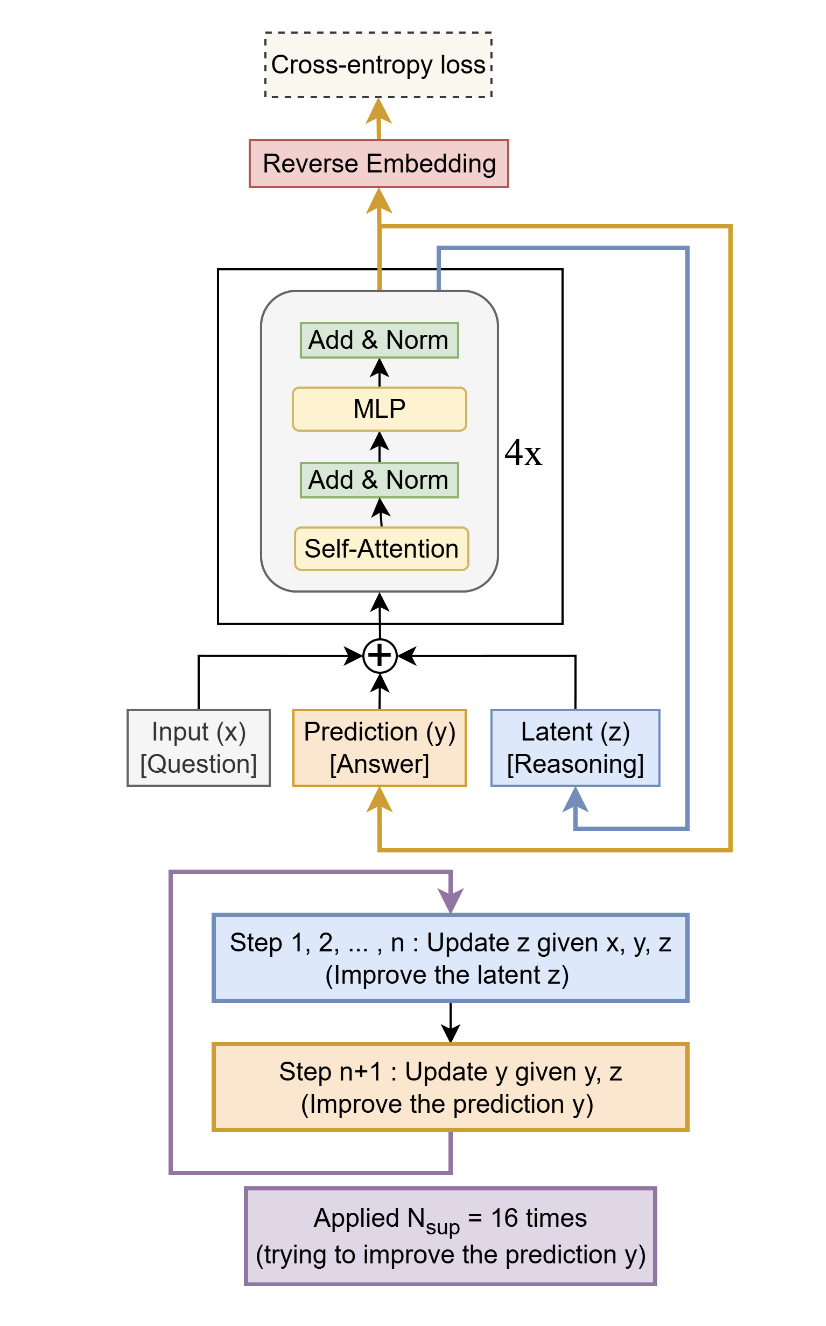
The model is fascinating and quite complex. It’s a recursive reasoning architecture with adaptive computation time (ACT), two interacting hidden states \(z_L\) and \(z_H\) and halting logic via Q-learning.
Data Flow
The model maintains two levels of latent states:
- \(z_H\): High-level state with shape
[batch_size, seq_len + puzzle_emb_len, hidden_size](i.e., the output \(y\) in this paper) - \(z_L\): Low-level state with the same shape as \(z_H\) (i.e., the output \(z\) in this paper)
┌─────────────────────────────────────────────────────────────┐
│ Forward Pass │
└─────────────────────────────────────────────────────────────┘
Input: batch = {inputs, puzzle_identifiers, targets}
carry = {z_H, z_L, steps, halted, current_data}
↓
┌─────────────────────────┐
│ Reset carry if halted │
│ z_H = H_init │
│ z_L = L_init │
└─────────────────────────┘
↓
┌─────────────────────────┐
│ Input Embeddings │
│ tokens + puzzle + pos │
└─────────────────────────┘
↓
┌─────────────────────────────────────┐
│ Recursive Reasoning (no grad) │
│ ┌─────────────────────────────┐ │
│ │ For h in range(H_cycles-1): │ │
│ │ For l in range(L_cycles): │ │
│ │ z_L ← L(z_L, z_H + x) │ │
│ │ z_H ← L(z_H, z_L) │ │
│ └─────────────────────────────┘ │
└─────────────────────────────────────┘
↓
┌─────────────────────────────────────┐
│ Final Reasoning Cycle (with grad) │
│ For l in range(L_cycles): │
│ z_L ← L(z_L, z_H + x) │
│ z_H ← L(z_H, z_L) │
└─────────────────────────────────────┘
↓
┌─────────────────────────┐
│ Output Generation │
│ logits = lm_head(z_H) │
│ q_halt = q_head(z_H₀) │
└─────────────────────────┘
↓
┌─────────────────────────┐
│ Halting Decision │
│ (ACT mechanism) │
└─────────────────────────┘
↓
Output: new_carry = {z_H', z_L', steps+1, halted', current_data}
outputs = {logits, q_halt_logits, q_continue_logits}
Q-Learning
Q-Learning is a reinforcement learning algorithm that learns to make decisions by estimating the quality Q-value of taking specific actions in specific states.
More specifically, if \(Q(state, action)\) is the expected future reward for taking action in state, then the Q-value of the optimal policy can be iteratively updated by the following Bellman equation:
\(Q(s, a) = Q(s, a) + \alpha [r + \gamma \max_{a'} Q(s', a') - Q(s, a)]\) where \(r\) is the reward for taking action \(a\) in state \(s\), \(\gamma\) is the discount factor, \(\alpha\) is the learning rate, \(s'\) is the next state, and \(a'\) is the next action.
The Q-value of the optimal policy is the maximum Q-value of all possible actions in all possible states.
\[Q^*(s, a) = \max_{a'} Q(s, a')\]Q-Learning in TRM
In TRM, the Q-learning is used to learn the halting policy, i.e., when to stop the reasoning process. More specifically, there are two actions need to be considered:
- Halt: Stop reasoning and return the output answer.
- Continue: perform one more reasoning cycle.
In the implementation, the Q-value is the output of the q_head of the model.
self.q_head = CastedLinear(self.config.hidden_size, 2, bias=True) # 2 actions: halt and continue
q_logits = self.q_head(z_H[:, 0]) # Using the first token of the high-level state as the state representation
q_halt_logits = q_logits[:, 0] # Q(state, halt)
q_continue_logits = q_logits[:, 1] # Q(state, continue)
The halting logic is implemented as follows:
if self.config.no_ACT_continue:
halted = (q_halt_logits > 0) # Halt if Q(halt) is positive
else:
halted = (q_halt_logits > q_continue_logits) # Halt if Q(halt) is greater than Q(continue)
Q-Learning Loss
The Q-learning loss is defined in the ACTLossHead class as below:
q_halt_loss = F.binary_cross_entropy_with_logits(
outputs["q_halt_logits"], # Predicted: should we halt?
seq_is_correct.to(...), # Target: 1 if sequence is correct, 0 otherwise
reduction="sum"
)
Where seq_is_correct is the target for the Q-learning loss, 1 if the model’s prediction is completely correct (all tokens match), 0 otherwise.
As noted, seq_is_correct is binary, either all tokens are correct or the sequence is wrong.
# Token-level correctness
mask = (labels != IGNORE_LABEL_ID) # Valid positions
is_correct = mask & (torch.argmax(outputs["logits"], dim=-1) == labels)
# Sequence-level correctness (ALL tokens must be correct)
loss_counts = mask.sum(-1) # Number of valid tokens per sequence
seq_is_correct = is_correct.sum(-1) == loss_counts # Boolean: all tokens correct?
Continue Loss
In addition, the authors also proposed to use the Q-Continue Loss (bootstrapped Q-values) (The question Should we continue? instead of Should we halt?).
However, as noted by the authors, while the Q-continue loss fits Q-learning, but seems totally unnecessary as the Q-halt loss is enough to learn the halting policy.
if "target_q_continue" in outputs:
q_continue_loss = F.binary_cross_entropy_with_logits(
outputs["q_continue_logits"], # Predicted: should we continue?
outputs["target_q_continue"], # Target: bootstrapped Q-value from next state
reduction="sum"
)
where target_q_continue is the bootstrapped Q-value from the next state.
target_q_continue = sigmoid(max(next_q_halt, next_q_continue))
Total loss
total_loss = lm_loss + 0.5 * (q_halt_loss + q_continue_loss)
where lm_loss is the standard cross-entropy on token predictions.
Training Dynamics of Q-Learning
Early phase: Init Q-head
The Q-head is initialized to (almost) zero for faster learning during bootstrapping, i.e., never halts early (always uses max steps). This forces the model to learn basic language understanding before adapting to the reasoning task.
# Q head special init
# Init Q to (almost) zero for faster learning during bootstrapping
with torch.no_grad():
self.q_head.weight.zero_()
self.q_head.bias.fill_(-5) # type: ignore
Phase 2: Learning to halt
As language understanding improves, seq_is_correct becomes more frequent and reliable, Q-head starts to learn correlation between reasoning state and correctness,
resulting in the model learning to halt early.
Phase 3: Exploration Refinement
# Force trying different step counts
min_halt_steps = random_int(2, halt_max_steps) with probability ε
The model exploration prevents the model always halts at the same step, thus leading to overfitting. This helps to discover optimal reasoning depth for different problems.
Applying to Relation Extraction problem
Relation Extraction (RE)
Relation Extraction (RE) is a core task in Natural Language Processing (NLP) that involves identifying and classifying semantic relationships between entities mentioned in text.
For example, given the sentence "John Smith is a patient of Dr. Emily Johnson", an RE system should detect the relationship between John Smith and Dr. Emily Johnson as "patient of".
Similarly, in the sentence "Aspirin is used to treat headache", the identified relationship is "used to treat" between two entities Aspirin and headache.
The set of possible relationships is typically predefined and fixed for a given task.
Importantly, the label "no relation" is also a valid category, indicating that no meaningful semantic link exists between the mentioned entities.
Traditional approaches to RE include rule-based methods, feature-based classifiers, and neural architectures leveraging contextual embeddings such as BERT. Recent advances, however, have explored formulating RE as a question answering (QA) problem, giving rise to methods such as QA4RE.
BioRED Dataset
The dataset used in this demo is the BioRED dataset. BioRED is a first-of-its-kind biomedical RE corpus with multiple entity types (e.g., gene/protein, disease, chemical) and relation pairs (e.g., gene-disease; chemical-chemical) at the document level, on a set of 600 PubMed abstracts. The data, pretrained models (for the RE task) and annotation guidelines are provided in the link: https://ftp.ncbi.nlm.nih.gov/pub/lu/BioRED/.
Data Format
The BioRED dataset adopts the PubTator format, a structured, plain-text representation commonly used for biomedical text annotations. Each document—typically a PubMed abstract—contains both text and text-bound annotations describing entities and relations. The format includes the following components:
- PMID: The PubMed identifier, followed by the document title and abstract text.
-
Entity annotations: Each entity is represented as
PMID \t start-index \t end-index \t text-span \t entity_type \t normalized_id. -
Relation annotations: Each relation is encoded as
PMID \t relation-type \t normalized_id1 \t normalized_id2 \t novelty.
An example of the PubTator-formatted document is shown below:
Example of PubTator-formatted document
15485686|t|A novel SCN5A mutation manifests as a ...
15485686|a|OBJECTIVE: Congenital long QT syndrome (LQTS) ...
15485686 8 13 SCN5A GeneOrGeneProduct 6331
15485686 56 72 long QT syndrome DiseaseOrPhenotypicFeature D008133
15485686 Association D001919 6331 Novel
15485686 Positive_Correlation D001919 p|SUB|V|1763|M Novel
Each document \(S\) may contain multiple entities \(E_i\) and relations \(R_{ij}\) between them. Importantly, no entity pair \((E_i, E_j)\) has more than one relation in the dataset—each pair is associated with at most a single relation \(R_{ij}\).
Thus, the task in BioRED can be defined as: given a document \(S\) and a set of entities \(E\), extract all relations \(R_{ij}\) that hold between entity pairs \((E_i, E_j)\) within the text.
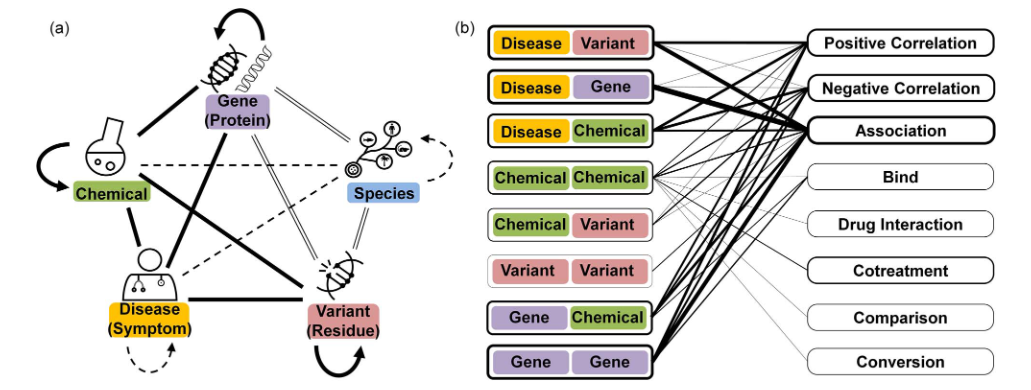
Entity Types
BioRED defines six entity types (five major biomedical categories and one infrequent type, Cell Line), each normalized to an external biomedical knowledge base. The entity taxonomy is summarized in the table below.
| Entity Type | Examples | Normalization Source |
|---|---|---|
| Gene (Protein) | ABCA1, CYP2D6, BMP | NCBI Gene |
| Variant (Residue) | S276T, rs2234671, c.435C>G | dbSNP |
| Species | Homo sapiens, E. coli | NCBI Taxonomy |
| Disease (Symptom) | Hypertension, Alzheimer’s disease | MEDIC (MeSH + OMIM) |
| Chemical | Terbutaline, Acetaminophen | MeSH: Chemicals and Drugs |
| Cell Line | MCF7/AdrR | Cellosaurus |
Entity types in BioRED and their corresponding normalization sources.
Relation Types
BioRED defines a comprehensive set of pairwise relations between concept types. Each relation is explicitly typed—either directional or non-directional—and falls into one of three major semantic categories: Positive Correlation, Negative Correlation, or Association. In addition to these, several specialized relation types capture more specific biomedical interactions, including Bind, Co-treatment, Comparison, Drug Interaction, and Conversion.
During dataset preprocessing, a special category labeled None is added to represent negative examples, denoting entity pairs with no annotated relationship.
Data Processing
In order to apply the TRM to the RE task, we need to convert the BioRED dataset into the format that can be used by the TRM. However, there are three main challenges making it is not straightforward:
- Variable Text Length. The current TRM expects a fixed length input (i.e., for the Sudoku puzzle, the input is a 9x9 grid), but biomedical texts vary greatly in length. We need to set a larger sequence length and truncate/padding the texts if necessary.
- Classification vs Generation task. The TRM is designed for the generation task, while the original RE task is a classification task. One of the approaches can be used is to convert the RE task into a multiple-choice generation task, where the model needs to generate the relation type options for the given entity pairs.
- Entity awareness. Unlike the Sudoku puzzle, the input in RE task contains the full text of the document and the entity pairs. In the dataset, one document may contain multiple entity pairs with multiple relations between them. Therefore, in order to answer specific relation type for a specific entity pair, the model needs to be aware of that entity pair, distinguish it from other entity pairs. Some potential solutions can be: adding special marker tokens around entities, use entity type embedding or create position-aware prompts. In this demon, we use the simplest solution, that is, adding special marker tokens around entities and move the two entities to the beginning of the input sequence.
The input format is shown below:
Input sequence:
[CLS] <E1> entity1_text </E1> [SEP] <E2> entity2_text </E2> [SEP]
full_text [SEP]
Options: A) Association B) PositiveCorrelation C) ... [SEP]
Label sequence:
[-100, -100, ..., -100, A, -100, -100, ...]
↑
Only supervise answer token
References
[1] Jolicoeur-Martineau, Alexia. “Less is More: Recursive Reasoning with Tiny Networks.” arXiv preprint arXiv:2510.04871 (2025).
[2] Luo, Ling, et al. “BioRED: a rich biomedical relation extraction dataset.” Briefings in Bioinformatics 23.5 (2022): bbac282.
Enjoy Reading This Article?
Here are some more articles you might like to read next: