Unlearning LLMs
- Introduction
- Motivation: Why Do We Need Unlearning?
- The Technical Setting
- Benchmarks: How to Evaluate Unlearning?
- Challenges in Unlearning LLMs
- Unlearning Methods
- Representation Misdirection for Unlearning (RMU)
- Adaptive RMU (On Effects of Steering Latent Representation for Large Language Model Unlearning - AAAI 2025)
- Negative Preference Optimization: From Catastrophic Collapse to Effective Unlearning (COLM 2023)
- LLM Unlearning via Loss Adjustment with Only Forget Data (ICLR 2025)
- A Closer Look at Machine Unlearning for Large Language Models (ICLR 2025)
- Large Language Models Unlearning
- References
Introduction
Machine unlearning is becoming a critical topic in the era of foundation models. As LLMs grow more powerful, they also become harder to control — and removing harmful, private, or outdated knowledge post‑training is increasingly important. In this post, we’ll take a deep dive into unlearning for LLMs: why it matters, how it’s measured, and the main approaches used in recent research.
We will cover:
- Motivation: Why unlearning is necessary and what risks it mitigates.
- Benchmarks & Metrics: Datasets and metrics that evaluate how well unlearning works.
- Methods: Key algorithmic approaches including gradient-based, optimization-based, and DPO‑based methods.
- Practical Challenges: Open problems, trade-offs, and future directions.
Motivation: Why Do We Need Unlearning?
Modern LLMs ingest massive datasets during pretraining, and as a result, they learn both desirable and undesirable information. There are several reasons to remove knowledge from an already‑trained model:
- Safety: Prevent the model from generating harmful or dangerous instructions (e.g., bomb-making guides).
- Privacy: Ensure memorized personal information (like phone numbers or medical records) can be erased upon request (GDPR “right to be forgotten”).
- Content moderation: Filter out toxic or biased outputs without fully retraining the model.
- Compliance: Adjust knowledge to match regulations or cultural norms across regions.
- Countering adversarial attacks: Current safeguards like refusal training [2] can be bypassed through adversarial attacks, and hazardous information can be reintroduced through finetuning. Similar to the case of enhancing inherent safety, unlearning especially when applied before model serving, can act as a countermeasure by removing the knowledge that these attacks or finetuning might exploit or reveal.
A naive approach would be to retrain from scratch without the sensitive data — but this is computationally infeasible for today’s LLMs. Instead, we seek unlearning: efficiently modifying the model so that it behaves as if it never saw the data we want to remove.
Refusal training:
Refusal training is a method that trains a model to decline or refuse to generate responses to prompts that are associated with malicious use cases.
This is typically achieved through (1) Supervised fine-tuning (SFT) with a dataset of pair harmful prompts with appropriate refusal responses, (2) RLHF with human preference data, (3) Adversarial training aiming to be more robust against adversarial prompts designed to bypass safety mechanisms. However, this method is still be circumvented by aversaries, such as posing harmful prompts in the past tense.
The Technical Setting
Before diving into methods, let’s define the core components used in a typical unlearning task. The process revolves around three key datasets:
- Forget set: \(\mathcal{D}_f\) (used in fine-tuning) This is a dataset of examples representing the knowledge that the unlearning process aims to remove from the language model, e.g., the WMDP benchmark [1] which contains hazardous knowledge in biosecurity and cybersecurity.
- Retain set: \(\mathcal{D}_r\) (used in fine-tuning) This is a dataset of examples representing general, benign knowledge that the unlearning process should aim to preserve. Recent works [3] try to remove the need of a retain set by using a “flat” loss adjustment approach which adjusts the loss function using only the forget data.
- Testing set: \(\mathcal{D}_t\) (used in evaluation) to evaluate two aspects: (1) unlearning performance - Question-Answering (QA) accuracy on WMDP benchmark, and (2) retaining performance - other benchmarks like MMLU and MT-Bench.
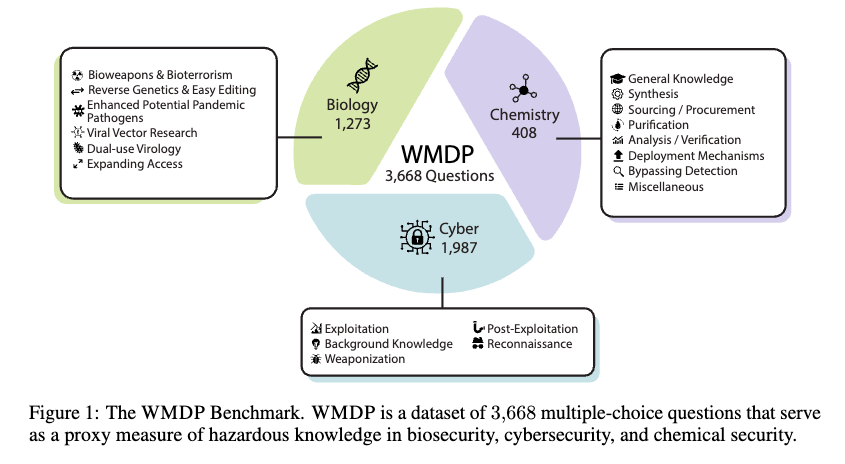
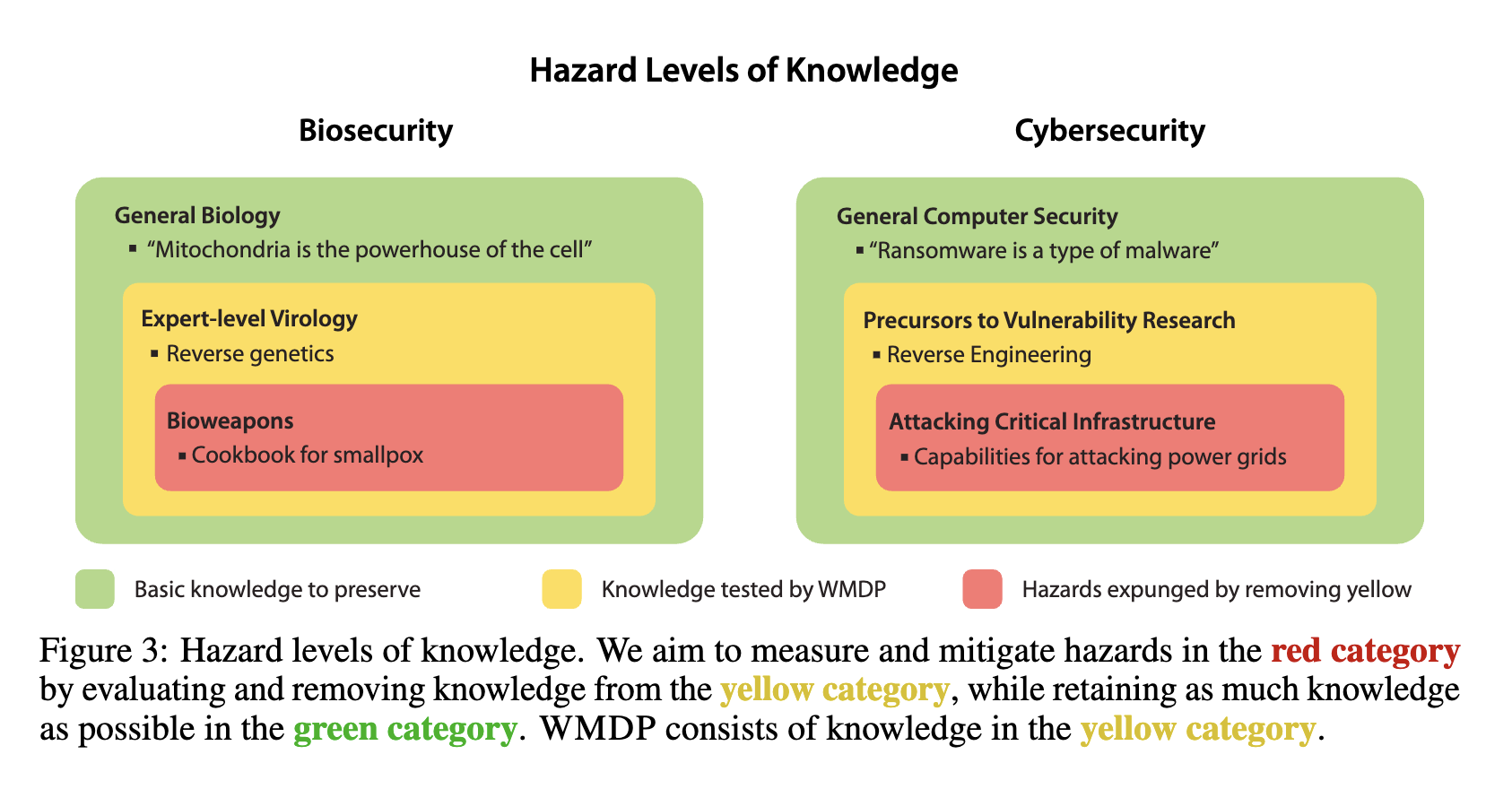
Benchmarks: How to Evaluate Unlearning?
To develop effective unlearning methods, we first need robust ways to measure unlearning success. There are three most common benchmarks: TOFU, MUSE and WMDP.
TOFU - A Task of Fictitious Unlearning for LLMs (COLM 2024)
Motivation
The TOFU benchmark introduces an interesting premise: unlearning fictitious, synthetic author profiles instead of real authors.
Why Fake/Fictitious Authors/Characters?
- How to know model after unlearning is equivalent to the model trained without that concept? \(\mathcal{U}(\mathcal{L}(\theta, \mathcal{D})) \stackrel{?}{=} \mathcal{L}(\theta, \mathcal{D} \setminus \mathcal{D}_F)\), where \(\mathcal{U}\) is the unlearning operator, \(\mathcal{L}\) is the learning operator that trains the model \(\theta\) on the dataset \(\mathcal{D}\).
- When unlearning real-world concepts, this question is impossible to answer because we can’t afford to retrain foundation models. With synthetic data, we can train a smaller model from scratch and compare.
This raises a key question: why should we care about this strict equality? This perspective comes from classical machine unlearning (often linked to differential privacy), where the goal is to provably forget a single data point. However, in the case of generative AI, I don’t think we should care the same. The goal is often functional (e.g., the model no longer outputs harmful information) rather than a perfect statistical match to a retrained model.
The dataset
Main features:
- 200 diverse synthetic author profiles, each consisting of 20 question-answer pairs. Subset of these profiles are used as the target forget set.
- Forget set: 2, 10 or 20 profiles depending on the setting.
- Retain set: Remaining fake profiles + Real authors (such as Shakespeare) + World Facts (such as the capital of France).
Examples:

Data Creation

Evaluation Metrics
-
Retain quality
- Probability Score Treat each question \(q\) as a multiple choice question with \(n\) options \(\{ a_1, a_2, ..., a_n \}\), the probability of the correct answer is \(p(a_i \mid q; \theta_u)\) should be the same as of the initial model \(p(a_i \mid q; \theta_o)\)
- ROUGE The model should be able to generate the same answer (with greedy sampling) as the initial model using the ROUGE-L recall score.
- Truth Ratio Can the model still provide the correct paraphrased answer? (e.g. “Paris is the capital of France” -> “France is the country with Paris as its capital”). What is the reason of having this metric? I guess it is because the most frequent/reasonable way to forget the target concept is not to provide a totally unrelated answer, but to phrasing the answer incorrectly.

-
Forget quality
- Challenge How to guarantee the model totally forget the target concept? Can “providing wrong answers about the target concept” be considered as good enough?
- In the paper, they use the Truth Ratio to measure the forget quality.
WMDP - Measuring and Reducing Malicious Use With Unlearning
Motivation:
- The Weapon Weapons of Mass Destruction Proxy Benchmark (WMDP),
MUSE - Machine Unlearning Six-Way Evaluation for Language Models (ICLR 2025)
While TOFU provides a solid foundation, its metrics don’t cover the full spectrum of real-world concerns like privacy and scalability. To address these limitations, the MUSE benchmark proposed a more comprehensive six-way evaluation.
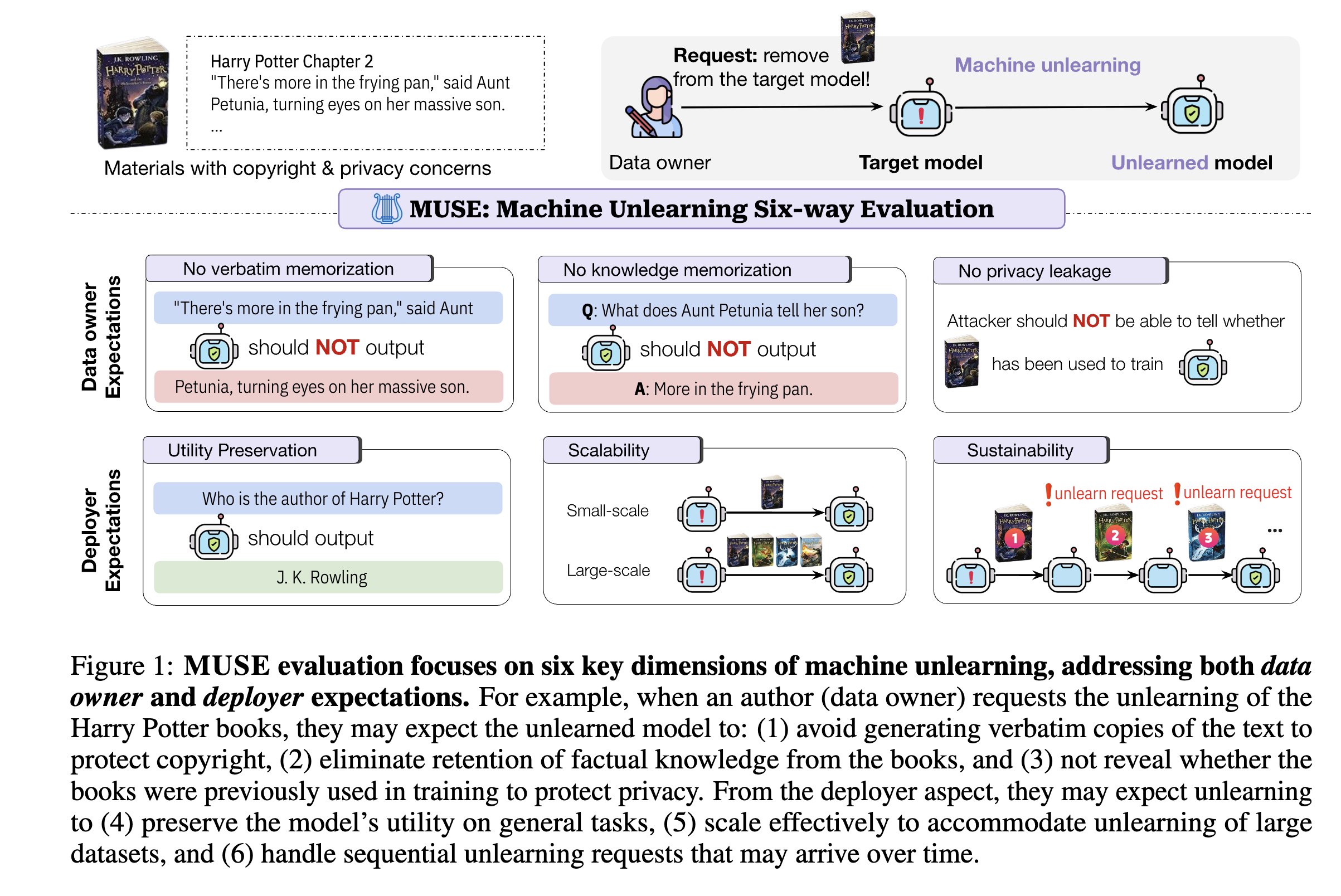

This paper present a new benchmark for evaluating the quality of machine unlearning, which considers six aspects:
- No verbatim memorization: The model should not exactly replicate any details from the forget set.
- No knowledge memorization: The model should be incapable of responding to questions about the forget set.
- No privacy leakage: It should be impossible to detect that the model was ever trained on the forget set.
- Utility preservation: The model should maintain high performance on the tasks it was trained for except for the forget set.
- Scalability: The method should be able to handle large forget set sizes.
- Substantiality: The method should be able to handle a large number of forget queries - continuous unlearning setting.
This benchmark highlights critical trade-offs: maintaining model utility, forgetting performance, and scalability.
Metrics for each aspect
Verbatim Memorization To measure verbatim memorization, the paper uses the ROUGE score between the model’s continuation and the actual continuation in the forget set:
\[\text{VerbMem}(f, \mathcal{D}) := \frac{1}{|\mathcal{D}_{\text{forget}}|} \sum_{x \in \mathcal{D}_{\text{forget}}} \text{ROUGE}(f(x_{[:l]}), x_{[l+1:]})\]ROUGE measures the overlap between the generated text (candidate) and one or more reference texts. It focuses on n-gram, sequence, and word-level similarity and is particularly recall-oriented, meaning it emphasizes how much of the reference text is captured by the generated text.
\[\text{ROUGE-N} = \frac{\sum_{r \in R} \sum_{\text{gram}_n \in r} \min \big( \text{Count}_{C}(\text{gram}_n), \text{Count}_{r}(\text{gram}_n) \big)}{\sum_{r \in R} \sum_{\text{gram}_n \in r} \text{Count}_{r}(\text{gram}_n)}\]- Numerator: number of overlapping (n)-grams between candidate and references
- Denominator: total number of (n)-grams in references
Special cases:
- ROUGE-1 → unigram overlap
- ROUGE-2 → bigram overlap
Knowledge Memorization
To measure knowledge memorization, the paper uses the ROUGE score between the model’s continuation and the actual continuation in the forget set:
\[\text{KnowMem}(f, \mathcal{D}_{\text{forget}}) := \frac{1}{|\mathcal{D}_{\text{forget}}|} \sum_{(q,a)\in\mathcal{D}_{\text{forget}}} \text{ROUGE}(f(q), a)\]Privacy Leakage
To measure privacy leakage, the paper uses (Min-K Prob) [6] a start-of-the-art MIA method to compute the standard AUC-ROC score of discriminating members \(\mathcal{D}_{\text{forget}}\) and non-members \(\mathcal{D}_{\text{holdout}}\) by using the logits of the last layer of the model.
\[\text{PrivLeak} := \frac{\text{AUC}(f_{\text{unlearn}}; \mathcal{D}_{\text{forget}}, \mathcal{D}_{\text{holdout}}) - \text{AUC}(f_{\text{retrain}}; \mathcal{D}_{\text{forget}}, \mathcal{D}_{\text{holdout}})}{\text{AUC}(f_{\text{retrain}}; \mathcal{D}_{\text{forget}}, \mathcal{D}_{\text{holdout}})}\]The good unlearning method should have \(\text{AUC}(f_{\text{unlearn}}; \mathcal{D}_{\text{forget}}, \mathcal{D}_{\text{holdout}}) \approx \text{AUC}(f_{\text{retrain}}; \mathcal{D}_{\text{forget}}, \mathcal{D}_{\text{holdout}})\) which means the unlearned model is indistinguishable from the original model. In contrast, the bad unlearning method will get a large positive or negative difference.
Min-K Prob [6]
The Min-K Prob is based on the hypothesis that a non-member example is more likely to include a few outlier words with low probability, while a member example is less likely to include such words.
Consider a sequence of tokens in a sentence, denoted as \(x = x_1, x_2, ..., x_N\), the log-likelihood of a token, \(x_i\), given its preceding tokens is calculated as \(\log p(x_i \mid x_1, ..., x_{i-1})\). We then select the \(k\%\) of tokens from \(x\) with the minimum token probability to form a set, Min-K%(x), and compute the average log-likelihood of the tokens in this set:
\[\text{MIN-K\% PROB}(x) = \frac{1}{E} \sum_{x_i \in \text{Min-K\%}(x)} \log p(x_i \mid x_1, ..., x_{i-1}).\]where \(E\) is the size of the Min-K%(x) set. We can detect if a piece of text was included in pretraining data simply by thresholding this MIN-K% PROB result.
Why this new benchmark is important?
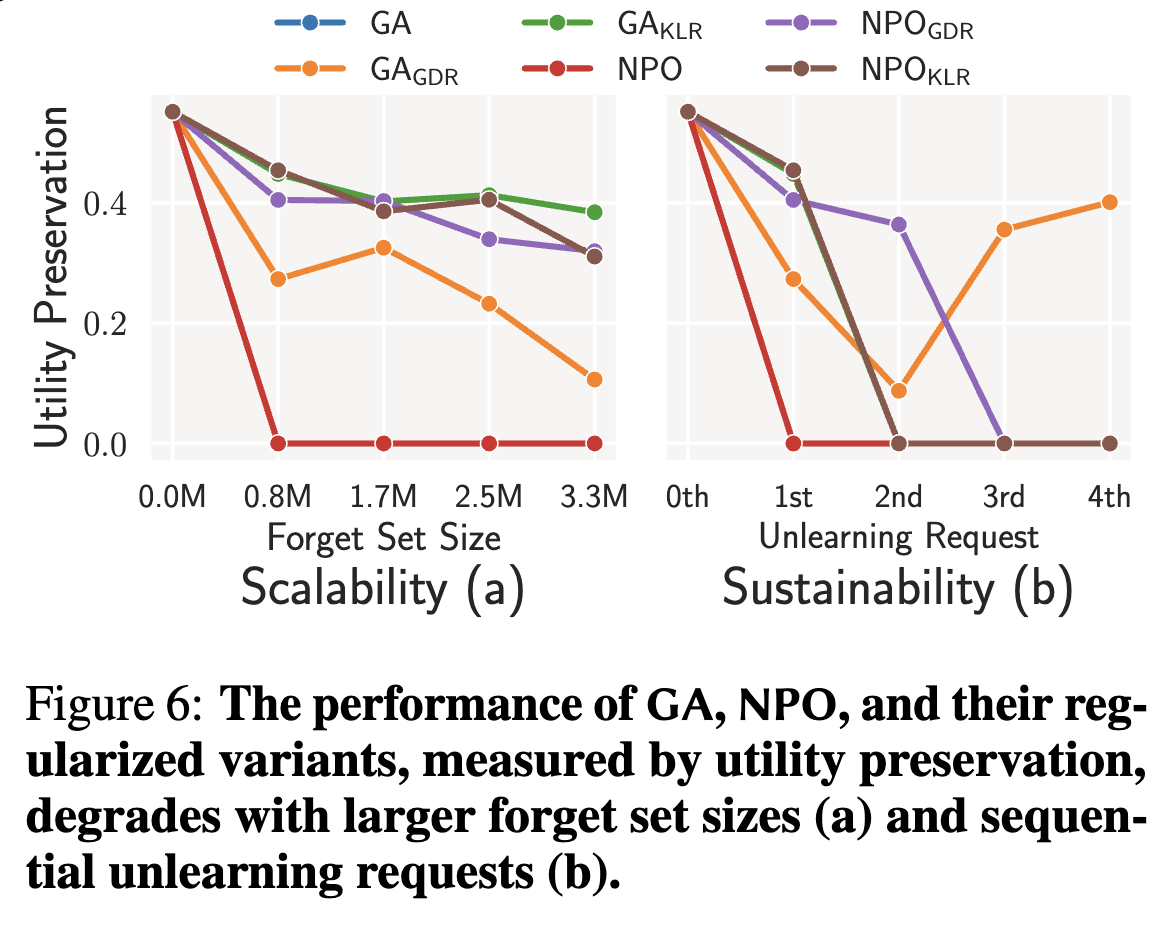
This benchmark provides another perspective - from model developer - who want to keep the model utility after unlearning. The current benchmark is more focused on the data owner’s expectation - forgetting the data - but not the model utility. With this benchmark, we can see that current unlearning methods are not good at these metrics:
- “Unlearning significantly degrades model utility”
- “Unlearning methods scale poorly with forget set sizes”
- “Unlearning methods cannot sustainably accommodate sequential unlearning requests”
Challenges in Unlearning LLMs
- Overlapping knowledge between the forget set and the retain set
- How to evaluate the unlearning performance How to know if the unlearning is successful?
Unlearning Methods
Now that we’ve seen how unlearning is measured, let’s explore some of the algorithmic approaches designed to achieve it.
A common formulation for unlearning is the following optimization problem:
\[\mathcal{L} = \min_{\theta} \underbrace{\mathbb{E}_{x^f \in \mathcal{D}_f} \ell(y^f|h_{\theta}^{(l)}(x^f))}_{\text{forget loss}} + \alpha \underbrace{\mathbb{E}_{x^r \in \mathcal{D}_r} \ell(y^r|h_{\theta}^{(l)}(x^r))}_{\text{retain loss}}\]where \(\theta\) is the model parameters of an autoregressive LLM \(f_{\theta}\), \(\ell\) is the loss function, \(y^f\) and \(y^r\) are the target representations (e.g., representations of next token) for the forget and retain sets, and \(\alpha\) is a hyperparameter.
It is worth noting that \(h_{\theta}^{(l)}\) is the average output hidden state of all tokens (with the size of sequence length) in forget-sample \(x^f \in \mathcal{D}_f\). Similarly, \(h_{\theta}^{(l)}\) is the average output hidden state of all tokens in retain-sample \(x^r \in \mathcal{D}_r\). Using this average representation to represent the entire forget-sample is one of current limitations that requires further investigation.
Intepretation: The goal is to maximize the loss on the forget set (encouraging the model to “unlearn” it, often by pushing its representations towards something random or nonsensical) while minimizing the loss on the retain set to keep its general knowledge intact.
Representation Misdirection for Unlearning (RMU)
Summary
This paper proposes a method to unlearn LLMs by steering the representation of forget samples towards a target random representation while keeping the representation of retain samples unchanged.
Approach
RMU [1] aims to steer model representation of forget samples (e.g., malicious use cases - that sampled from the forget set) in the intermediate layer towards a target random representation while keeping the representation of retain samples (e.g., benign use cases - that sampled from the retain set) unchanged.
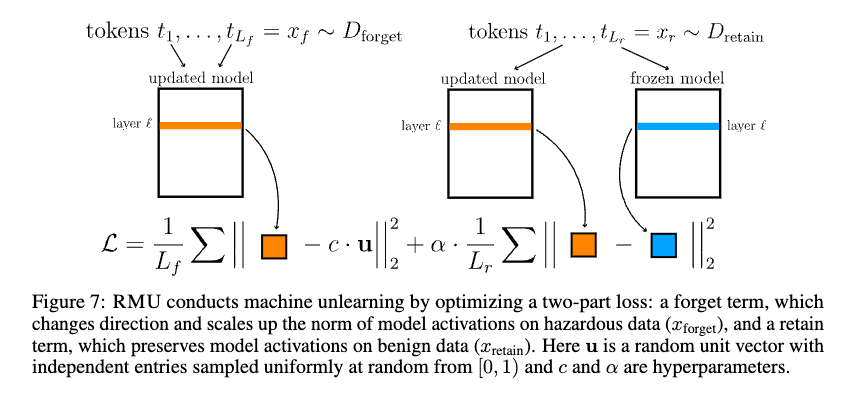
More specifically, given a forget set \(\mathcal{D}_f\) and a retain set \(\mathcal{D}_r\), and a frozen model \(h_{\theta^{\text{frozen}}}\) with parameters \(\theta^{\text{frozen}}\), RMU steers the latent representation of forget-tokens to a predetermined random representation \(y^f = cu\), where \(u\) is a random unit vector each element is sampled from Uniform distribution \(U(0,1)\), \(c \in \mathbb{R}^+\) is a coefficient, and regularizes the latent representation of retain-tokens back to the frozen model’s representation. The loss of RMU is
\[\mathcal{L} = \mathbb{E}_{x^f \in \mathcal{D}_f} \|h_{\theta^{\text{rm}}}^{(l)}(x^f) - cu\|^2 + \alpha\mathbb{E}_{x^r \in \mathcal{D}_r} \|h_{\theta^{\text{rm}}}^{(l)}(x^r) - h_{\theta^{\text{frozen}}}^{(l)}(x^r)\|^2,\]where \(\theta^{\text{rm}}\) is the parameters of the model to be optimized, and \(\alpha\) is a hyperparameter.
Implementation
- Official Github repo: https://github.com/centerforaisafety/wmdp
The minimal code of this project is as follows:
Control vector (\(u\)) generation. Each data point in the forget set is associated with a control vector:
control_vectors_list = []
for i in range(len(forget_data_list)):
random_vector = torch.rand(1,1, updated_model.config.hidden_size, dtype=updated_model.dtype, device=updated_model.device)
control_vec = random_vector / torch.norm(random_vector) * args.steering_coeff_list[i]
control_vectors_list.append(control_vec)
Get the forget and retain activations/losses:
unlearn_inputs = tokenizer(unlearn_batch, return_tensors="pt", padding=True, truncation=True, max_length=max_length)
updated_forget_activations = forward_with_cache(updated_model, unlearn_inputs, module=updated_module, no_grad=False)
unlearn_loss = torch.nn.functional.mse_loss(updated_forget_activations, control_vec)
# similar for retain
Forward with cache - to get the activations from updated model or frozen model. The module is the layer of the model that we want to get the activations from.
frozen_module = eval(args.module_str.format(model_name="frozen_model", layer_id=args.layer_id))
def forward_with_cache(model, inputs, module, no_grad=True):
# define a tensor with the size of our cached activations
cache = []
def hook(module, input, output):
if isinstance(output, tuple):
cache.append(output[0])
else:
cache.append(output)
return None
hook_handle = module.register_forward_hook(hook)
if no_grad:
with torch.no_grad():
_ = model(**inputs)
else:
_ = model(**inputs)
hook_handle.remove()
return cache[0]
Evaluation Implementation
The evaluation is done using the lm-eval-harness framework
!lm-eval --model hf \
--model_args pretrained="checkpoints/rmu/adaptive_HuggingFaceH4/zephyr-7b-beta_alpha-1200-1200_coeffs-6.5-6.5_batches-500_layer-7_scale-5" \
--tasks mmlu,wmdp \
--batch_size=16
Basically, it will load the pretrained unlearned model and evaluate it on the MMLU and WMDP tasks.
Adaptive RMU (On Effects of Steering Latent Representation for Large Language Model Unlearning - AAAI 2025)
Summary
This paper proposes a layer-adaptive RMU method, which uses a different \(c\) for each layer.
Key Observation
This paper points out an interesing phenomenon that the performance of RMU is sensitive to the choice of coefficient \(c\) in the above loss function.
More specifically, the random unit vector \(u\) and the representation of forget samples \(\hat{h}_{\theta^{\text{rm}}}^{(l)}(x^f)\) are more aligned as \(c\) increases, suggesting the better unlearning performance.
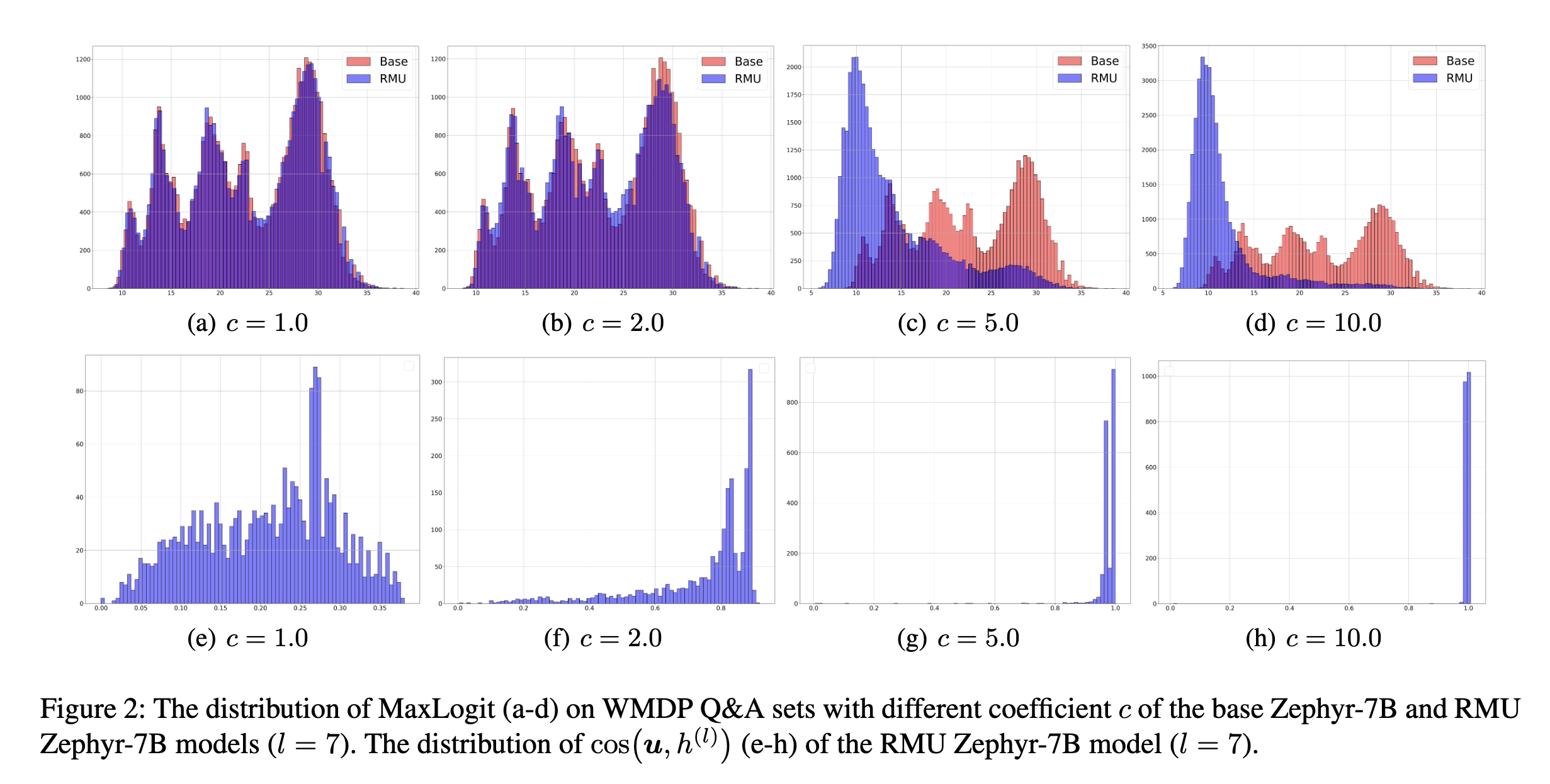
However, using a fixed \(c\) across all layers is not ideal, since the performance of RMU is observed to be layer-dependent. More specifically, as discussed in Section 4.3 in [4], within early layers, the \(l^2\) norm of the representation of forget samples is relatively smaller than the coefficient \(c\) and during the unlearning process, that norm exponentially grows and appproaches \(c\), thereby facilitating the convergence of the unlearning process. However, in later layer, the \(l^2\) norm of the representation of forget samples is initially larger than \(c\) and remains unchanged during unlearning, making the unlearning process less effective.
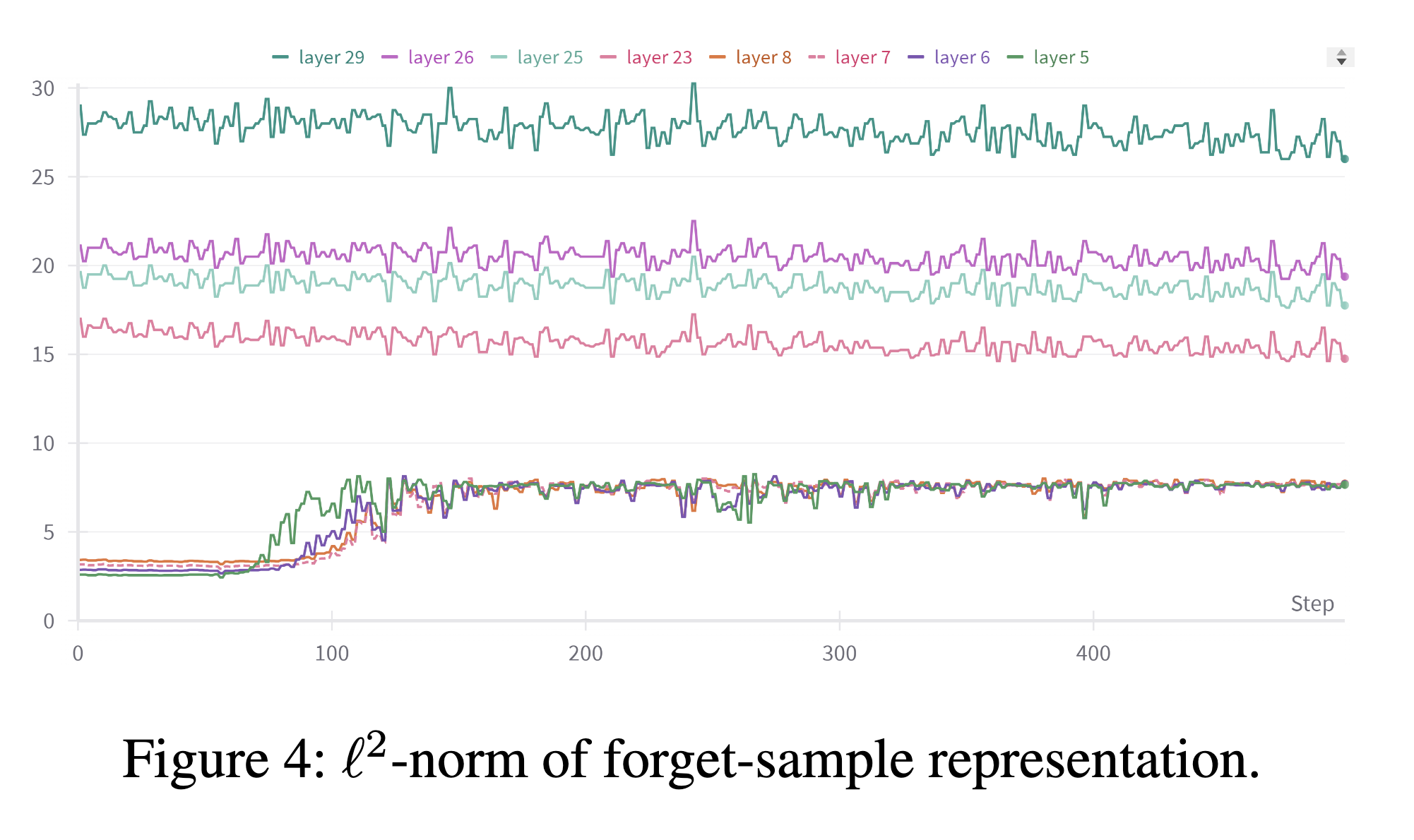
Inspired by the above observation, this paper proposes a layer-adaptive RMU method, which uses a different \(c\) for each layer.
\[\mathcal{L}^{\text{adaptive}} = \underbrace{\mathbb{E}_{x_F \in \mathcal{D}_{\text{forget}}} \|h_{\theta^{\text{unlearn}}}^{(l)}(x_F) - \beta\|h_{\theta^{\text{frozen}}}^{(l)}(x_F)\| \|u\|_2^2}_{\text{adaptive forget loss}} + \underbrace{\alpha \mathbb{E}_{x_R \in \mathcal{D}_{\text{retain}}} \|h_{\theta^{\text{unlearn}}}^{(l)}(x_R) - h_{\theta^{\text{frozen}}}^{(l)}(x_R)\|_2^2}_{\text{retain loss}}\]where \(\beta \|h_{\theta^{\text{frozen}}}^{(l)}(x_F)\|\) is the adaptive scaling coefficient for the forget loss which is computed by the norm of the representation of forget samples in the corresponding layer of the frozen model.
However, it is worth noting that intuitively, the higher \(c\) leads to a more alignment between forget representation and the random unit vector \(u\), which suggests the better unlearning performance - more randomness of the output with the forget prompt. However, it also leads to a worse retaining performance.
Implementation
- Official Github repo: https://github.com/RebelsNLU-jaist/llm-unlearning
Adaptive RMU is heavily adapted from the RMU codebase. Following is the minimal code of the adaptive RMU, which only differs in the loss function:
Recall the code from RMU:
unlearn_inputs = tokenizer(unlearn_batch, return_tensors="pt", padding=True, truncation=True, max_length=max_length)
updated_forget_activations = forward_with_cache(updated_model, unlearn_inputs, module=updated_module, no_grad=False)
unlearn_loss = torch.nn.functional.mse_loss(updated_forget_activations, control_vec)
# similar for retain
From Adaptive RMU:
updated_forget_activations = forward_with_cache(updated_model, unlearn_inputs, module=updated_module, no_grad=False)
if idx == 0:
coeffs["0"] = torch.mean(updated_forget_activations.norm(dim=-1).mean(dim=1), dim=0).item() * args.scale
elif idx == 1:
coeffs["1"] = torch.mean(updated_forget_activations.norm(dim=-1).mean(dim=1), dim=0).item() * args.scale
else:
pass
unlearn_loss = torch.nn.functional.mse_loss(updated_forget_activations, control_vec * coeffs[f"{topic_idx}"])
topic_idx is the index of the forget topic (either wmdp-bio or wmdp-cyber). The author’s code is not optimized yet :v.
Negative Preference Optimization: From Catastrophic Collapse to Effective Unlearning (COLM 2023)
Discussion about DPO can be found in my NLP foundation blog post.
Preference Optimization. In preference optimization (Ouyang et al., 2022; Bai et al., 2022; Stiennon et al., 2020; Rafailov et al., 2024), we are given a dataset with preference feedbacks \(\mathcal{D}_{\text{paired}} = \{(x_i, y_{i,w}, y_{i,l})\}_{i \in [n]}\), where \((y_{i,w}, y_{i,l})\) are two responses to \(x_i\) generated by a pre-trained model \(\pi_\theta\), and the preference \(y_{i,w} \succ y_{i,l}\) is obtained by human comparison (here “w” stands for “win” and “l” stands for “lose” in a comparison). The goal is to fine-tune \(\pi_\theta\) using \(\mathcal{D}_{\text{paired}}\) to better align it with human preferences. A popular method for preference optimization is Direct Preference Optimization (DPO) (Rafailov et al., 2024), which minimizes
\[\mathcal{L}_{\text{DPO},\beta}(\theta) = -\frac{1}{\beta}\mathbb{E}_{\mathcal{D}_{\text{paired}}} \left[ \log \sigma \left( \beta \log \frac{\pi_\theta(y_w \mid x)}{\pi_{\text{ref}}(y_w \mid x)} - \beta \log \frac{\pi_\theta(y_l \mid x)}{\pi_{\text{ref}}(y_l \mid x)} \right) \right]\]Here, \(\sigma(t) = 1/(1 + e^{-t})\) is the sigmoid function, \(\beta > 0\) is the inverse temperature, and \(\pi_{\text{ref}}\) is a reference model.
Unlearning as preference optimization. We observe that the unlearning problem can be cast into the preference optimization framework by treating each \((x_i, y_i) \in \mathcal{D}_{\text{FG}}\) as only providing a negative response \(y_{i,l} = y_i\) without any positive response \(y_{i,w}\). Therefore, we ignore the \(y_w\) term in DPO in Eq. (2) and obtain the Negative Preference Optimization (NPO) loss:
\[\mathcal{L}_{\text{NPO},\beta}(\theta) = -\frac{2}{\beta}\mathbb{E}_{\mathcal{D}_{\text{FG}}} \left[ \log \sigma \left( - \beta \log \frac{\pi_\theta(y \mid x)}{\pi_{\text{ref}}(y \mid x)} \right) \right] = -\frac{2}{\beta}\mathbb{E}_{\mathcal{D}_{\text{FG}}} \left[ \log \left( 1 + \left( \frac{\pi_\theta(y \mid x)}{\pi_{\text{ref}}(y \mid x)} \right)^\beta \right) \right]\]Minimizing \(\mathcal{L}_{\text{NPO},\beta}\) ensures that the prediction probability on the forget set \(\pi_\theta(y_i \mid x_i)\) is as small as possible, aligning with the goal of unlearning the forget set.
Implementation
- DPO official Github repo: https://github.com/eric-mitchell/direct-preference-optimization
- NPO official Github repo: https://github.com/licong-lin/negative-preference-optimization
Because of the similarity between DPO and NPO, in the following, I will only show the code for DPO.
In the train.py file, we create the policy and reference models, and call the trainer to train the policy model. Note that, we disable the dropout of the policy and reference models. In the trainer, we also set the reference model to eval mode.
The DPO loss. Note that, this code also support the IPO (Inverse Preference Optimization) loss.
def dpo_loss(self, policy_chosen_logps, policy_rejected_logps, reference_chosen_logps, reference_rejected_logps, beta, ipo, reference_free, label_smoothing):
pi_logratios = policy_chosen_logps - policy_rejected_logps
ref_logratios = reference_chosen_logps - reference_rejected_logps
if reference_free:
ref_logratios = 0
logits = pi_logratios - ref_logratios # also known as h_{\pi_\theta}^{y_w,y_l}
if ipo:
losses = (logits - 1/(2 * beta)) ** 2 # Eq. 17 of https://arxiv.org/pdf/2310.12036v2.pdf
else:
# Eq. 3 https://ericmitchell.ai/cdpo.pdf; label_smoothing=0 gives original DPO (Eq. 7 of https://arxiv.org/pdf/2305.18290.pdf)
losses = -F.logsigmoid(beta * logits) * (1 - label_smoothing) - F.logsigmoid(-beta * logits) * label_smoothing
chosen_rewards = beta * (policy_chosen_logps - reference_chosen_logps).detach()
rejected_rewards = beta * (policy_rejected_logps - reference_rejected_logps).detach()
The policy_chosen_logps and policy_rejected_logps are the log probabilities of the chosen and rejected responses of the policy model, respectively. Similar for the reference_chosen_logps and reference_rejected_logps, with one difference is that we don’t need to trace the gradients of the reference model.
policy_chosen_logps, policy_rejected_logps = self.concatenated_forward(self.policy, batch)
with torch.no_grad():
reference_chosen_logps, reference_rejected_logps = self.concatenated_forward(self.reference_model, batch)
The concatenated_forward function is to get the log probabilities of the chosen and rejected responses of the policy and reference models. To get the log probabilities, we need to use the attention mask because we want to ignore padding tokens when computing the log probability of a sequence. The attention mask ensures that:
- Padding tokens don’t contribute to the forward pass computation
- We only sum log probabilities over actual response tokens (not padding)
This is crucial because sequences are batched together and padded to the same length, but we only want to evaluate the model on real tokens, not padding.
def get_log_probs(logits, labels):
"""Get log probability of labels under the model's logits."""
# Shift: predict next token
logits = logits[:, :-1, :] # Remove last prediction
labels = labels[:, 1:] # Remove first label (no prediction for it)
# Mask out padding tokens (marked as -100)
mask = (labels != -100)
labels[labels == -100] = 0 # Replace -100 with valid index
# Get log prob for each token
log_probs = logits.log_softmax(-1)
token_log_probs = log_probs.gather(dim=2, index=labels.unsqueeze(2)).squeeze(2)
# Sum only over non-padding tokens
return (token_log_probs * mask).sum(-1)
LLM Unlearning via Loss Adjustment with Only Forget Data (ICLR 2025)
Summary
This paper proposes a method to unlearn LLMs by adjusting the loss function using only the forget data.
Motivation - Eliminating the need for a retain set
Previous unlearning methods typically require a retain set or a reference model to maintain the performance of the unlearned model on the retain set. The limitation of this requirement (as stated in [3]) is that it is may lead to a trade-off between model utility and forget performance (why?). Furthermore, fine-tuning using both retain data and forget data would require a careful design of a data mixing strategy to avoid information leakage from the retain set to the forget set.
Loss-Adjustments via f-divergence Maximization
For each learning batch, we assume that we only have access to a set of forget samples \((x_f, y_f) \in D_f\). Instead of directly adopting gradient ascent over these forget samples, we propose to maximize the divergence between exemplary and bad generations of forget data. Key steps are summarized as below.
Step 1: Equip example/template responses \(y_e\) for each forget sample \(x_f\). Together we denote the paired samples as \(D_e = \{(x_f^j, y_e^j)\}_{j\in[N]}\).
-
This could be done by leveraging open-source LLMs such as Llama 3.1 [25] or self-defining the responses according to our wish, etc. The designated unlearning response could be a reject-based answer such as “I don’t know” (denoted as “IDK”) or an irrelevant answer devoid of the unlearning target-related information.
-
Motivation: Step 1 generates example responses for LLM fine-tuning and provides better instructions on what LLM should respond given the forget data. Besides, certain existing methods make LLM generate hallucinated responses after unlearning, which further illustrates the importance of example responses for LLM unlearning.
Step 2: Loss adjustments w.r.t. the sample pairs \((x_f, y_e, y_f)\) through:
\[L(x_f, y_e, y_f; \theta) = \lambda_e \cdot L_e(x_f, y_e; \theta) - \lambda_f \cdot L_f(x_f, y_f; \theta),\]where \(L_e, L_f\) are losses designed for the data sample \((x_f, y_e)\) and \((x_f, y_f)\), respectively.
- Motivation: Step 2 encourages the LLM to forget the forget data with bad responses, meanwhile, learn to generate good responses on relevant forget data [such as template answers].
Step 3: How to decide on the values of \(\lambda_e\) and \(\lambda_f\)?
We leverage f-divergence to illustrate the appropriate balancing between \(L_e(x_f, y_e; \theta)\) and \(L_f(x_f, y_f; \theta)\). Assume \(x_f, y_e\) is generated by the random variable \(X_f, Y_e\) jointly following the distribution \(\mathcal{D}_e\). Similarly, \(x_f, y_f\) is given by \(X_f, Y_f\) and \((X_f, Y_f) \sim \mathcal{D}_f\). Step 2 shares similar insights as if we are maximizing the divergence between \(\mathcal{D}_e\) and \(\mathcal{D}_f\). Our theoretical purpose is to obtain the model that maximizes the f-divergence between \(\mathcal{D}_e\) and \(\mathcal{D}_f\), defined as \(f_{div}(\mathcal{D}_e\|\mathcal{D}_f)\).
The variational form f-divergence: Instead of optimizing the \(f_{div}\) term directly, we resolve to the variational form of it. Due to the Fenchel duality, we would have:
\[f_{div}(\mathcal{D}_e\|\mathcal{D}_f) = \sup_g [\mathbb{E}_{z_e\sim\mathcal{D}_e} [g(z_e)] - \mathbb{E}_{z_f\sim\mathcal{D}_f} [f^*(g(z_f))]] := \sup_g \text{VA}(\theta, g),\]we define \(f^*\) as the conjugate function of the f-divergence function. For simplicity, we define \(\text{VA}(\theta, g^*) := \sup_g \text{VA}(\theta, g)\), where \(g^*\) is the optimal variational function.
Connection with DPO
Direct Preference Optimization (DPO) is a method to align LLMs with human preferences, however, unlike PPO which uses a reward model, DPO simplifies PPO by directly optimizing the policy model to adhere to human preferences without the need for a reward model. In the context of unlearning, DPO can be used to unlearn the LLM by directly optimizing the original model to align forget prompt with the template response.
Given a dataset \(D = \{(x_f^j, y_e^j, y_f^j)\}_{j\in[N]}\), where \(y_e\) and \(y_f\) are preferred template and original forget responses to the forget prompt \(x_f\), DPO fine-tunes original model \(\theta_o\) using \(D\) to better align it with good answer preferences, which minimizes:
\[L_{\text{DPO},\beta}(\theta) = -\frac{2}{\beta}\mathbb{E}_D\left[\log \sigma\left(\beta\log \frac{\pi_\theta(y_e \mid x_f)}{\pi_{\text{ref}}(y_e \mid x_f)} - \beta\log \frac{\pi_\theta(y_f \mid x_f)}{\pi_{\text{ref}}(y_f \mid x_f)}\right)\right]\] \[= -\frac{2}{\beta}\mathbb{E}_D\left[\log \sigma\left(\beta(\log \prod_{i=1}^{\mid y_e \mid}h_\theta(x_f, y_e,_{<i}) - \log \prod_{i=1}^{\mid y_f \mid}h_\theta(x_f, y_f,_{<i}))-M_{\text{ref}}\right)\right],\]where, \(\sigma(t) = \frac{1}{1+e^{-t}}\) is the sigmoid function, \(\beta > 0\) is the inverse temperature, \(\pi_\theta := \prod_{i=1}^{\mid y \mid} h_\theta(x, y_{<i})\) is the predicted probability of the response \(y\) to prompt \(x\) given by LLM \(\theta\), \(\pi_{\text{ref}}\) is the predicted probability given by reference model, and \(M_{\text{ref}} := \beta(\log \prod_{i=1}^{\mid y_e \mid}h_{\theta_o}(x_f, y_{e,i}) - \log \prod_{i=1}^{\mid y_f \mid}h_{\theta_o}(x_f, y_{f,i}))\).
Intepretation: minimizing \(L_{\text{DPO},\beta}(\theta)\) is equivalent to maximizing \(\log \prod_{i=1}^{\mid y_e \mid}h_\theta(x_f, y_e,_{<i})\) - which is the log probability of the template response - while minimizing \(\log \prod_{i=1}^{\mid y_f \mid}h_\theta(x_f, y_f,_{<i})\) - that of the forget response. the \(M_{\text{ref}}\) term is a constant w.r.t. \(\theta\) which is the gap between two log probabilities of the template and forget responses given by the reference model - so that the optimal should maintain the same gap as the reference model (IMO: should add max-margin loss here).
FLAT
As for FLAT, we calculate the average probability of all correctly generated tokens and employ a novel re-weighting mechanism that assigns different importance to each term using distinct activate functions for both the example and forget loss terms, which minimizes:
\[L_{\text{FLAT}}(\theta) = -\mathbb{E}_D\left[g^*\left(\frac{1}{\mid y_e \mid} \sum_{i=1}^{\mid y_e \mid}h_\theta(x_f, y_{e,<i})\right) - f^*(g^*\left(\frac{1}{\mid y_f \mid} \sum_{i=1}^{\mid y_f \mid}h_\theta(x_f, y_{f,<i})\right))\right].\]Here, \(f^*(\cdot), g^*(f^*(\cdot))\) are the activate functions that assign appropriate weights to each loss term. The detailed derivation is in Appendix B.2 in the paper. Specifically, DPO relies on a reference model to guide the unlearning process, whereas FLAT only uses a sample pair dataset containing both exemplar and forget responses. Besides, FLAT differs from DPO in three critical aspects: the re-weighting activation function, whether to sum or average the token losses, and whether to apply the logarithm to the output probability.
An example (from Appendix B.2 in the paper) is as follows:
Here, \(v\) is the vocabulary size, \(y_{e,i,k}\) is the \(k\)-th element of vector representing the \(i\)-th token in the good response \(y_e\), \(y_{f,i,k}\) is the \(k\)-th element of vector representing the \(i\)-th token in the forget response \(y_f\). Additionally, \(h_\theta(x_f, y_{e,<i})_k\) and \(h_\theta(x_f, y_{f,<i})_k\) denote the \(k\)-th entry of the probability distribution for the correctly generated token.
For KL f-divergence, \(f^*(u) = e^{u-1}, g^*(v) = v\), hence, \(g^*(\mathbb{P}(x_f, y_e; \theta)) - f^*(g^*(\mathbb{P}(x_f, y_f; \theta))) = \mathbb{P}(x_f, y_e; \theta) - e^{\mathbb{P}(x_f, y_f; \theta)-1}\). We have:
\[L_{\text{FLAT}}(\theta) = -\mathbb{E}_D\left[\frac{\sum_{i=1}^{ \mid y_e \mid} h_\theta(x_f, y_{e,<i})}{\mid y_e \mid} - e^{\frac{\sum_{i=1}^{ \mid y_f \mid} h_\theta(x_f, y_{f,<i})}{\mid y_f \mid}-1}\right].\]Implementation
- Official Github repo: https://github.com/UCSC-REAL/FLAT
A Closer Look at Machine Unlearning for Large Language Models (ICLR 2025)
Summary
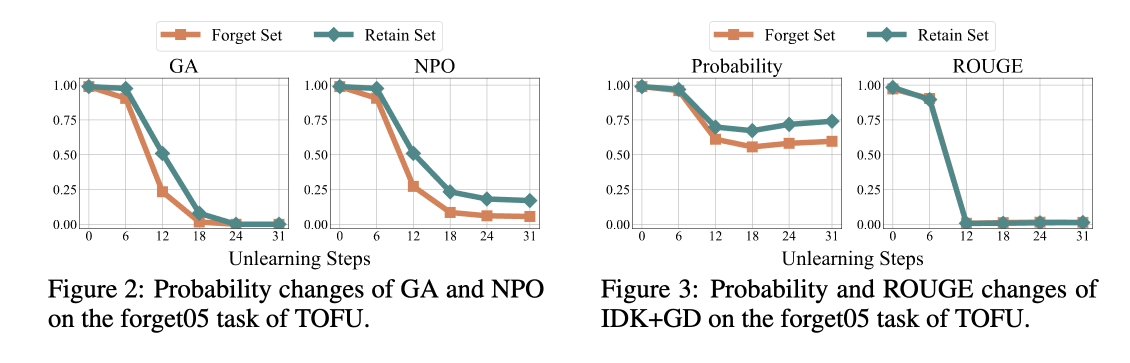
This paper investigates the effectiveness of unlearning LLMs for targeted and untargeted use cases. It proposes a Maximizing Entropy (ME) objective for untargeted unlearning and Answer-Preservation (AP) objective for targeted unlearning.
Untargeted vs Targeted Unlearning
Targeted unlearning hopes to make a specified template response to the questions in the forget set, while untargeted unlearning only requires not leaking the contents of the forget set. Mathematically, the loss function for untargeted unlearning is (borrowing the notation of DPOfrom [3])
\[= -\frac{2}{\beta}\mathbb{E}_D\left[\log \sigma\left(\beta(\log \prod_{i=1}^{\mid y_e \mid}h_\theta(x_f, y_e,_{<i}) - \log \prod_{i=1}^{\mid y_f \mid}h_\theta(x_f, y_f,_{<i}))-M_{\text{ref}}\right)\right],\]Where \(y_e\) is the template response and \(y_f\) is the forget response. Targeted unlearning aims to make the model response to the forget set to be close to the template response, hence, maximizing the probability of the template response. On the other hand, untargeted unlearning only requires the model response to the forget set to be far from the forget response, hence, minimizing the probability of the forget response.
Maximizing Entropy for Untargeted Unlearning
The paper states that “the core of most untargeted unlearning methods is to adapt a gradient ascent direction that maximizes the prediction loss over the forget set - may have several challenges”.
- The behavior of the ideal retain model is unpredictable: The cost to retrain the model from scratch is extremely expensive in the case of LLMs. More importantly, gradient ascent on the forget set when retraining may lead to unpredicatable behavior of the model.
- Potential hallucinations in the surrogate retain model: An alternative approach for the expensive retraining is to use a surrogate model - which is a base model such as Llama 2, fine-tuned on a small fictitious dataset \(\mathcal{D}^f = \{ \mathcal{D}^f_F, \mathcal{D}^f_R \}\), where \(\mathcal{D}^f_F\) and \(\mathcal{D}^f_R\) are the forget and retain sets, respectively. However, this approach may lead to hallucinations, where the model generates responses that are not present in the retain set.
Idea: Align the prediction behavior of the unlearned model on the forget set with that of a randomly initialized model.
- The randomly initialized model is data-independent and does not contain any knowledge about the forget set, avoids the leakage of relevant information.
- The behavior of the randomly initialized model is random guessing - maximizing the entropy of the output distribution.
where \(P_t = p(x'_t \mid x'_{<t}; \theta)\) is the predicted probability for the \(t\)-th token in \(x' = x \circ y\) and \(\mathcal{U}_{[K]}\) is a uniform distribution over the vocabulary of size \(K\), where each value is \(1/K\).
Minimizing above loss is equivalent to Maximizing Entropy (ME) of predicted distribution for each next token. The greater the entropy, the higher the uncertainty of the prediction, indicating that the model behaves closer to a randomly initialized model for random guessing. This objective also avoids catastrophic collapse caused by the unbounded forget loss (Zhang et al., 2024a; Ji et al., 2024).
Mitigate Excessive Ignorance of Targeted Unlearning
Over Ignorance Issue: Refuse to answer most questions in the retain set - False Positive. It is due to (based on their argument) that \((\mathcal{X}_F, \mathcal{Y}_F) \approxeq (\mathcal{X}_R, \mathcal{Y}_R)\), therefore, increasing \(P(\mathcal{Y}_{IDK} \mid \mathcal{X}_F)\) will also increase \(P(\mathcal{Y}_{IDK} \mid \mathcal{X}_R)\).
Their experiment to support the above argument is as follows:
Answer-Preservation (AP):
Intuitively, given a question in the retain set, the regularization loss for targeted unlearning should satisfy two objectives:
- Reduce the probability of the rejection template.
- Maintain the probability of the original answer.
Thus, the authors propose the Answer Preservation (AP) loss as follows:
\[\mathcal{L}_{\text{AP}}(\mathcal{D}_R, \mathcal{D}_{\text{IDK}}; \theta) = -\frac{1}{\beta}\mathbb{E}_{(x,y)\sim\mathcal{D}_R,y'\sim\mathcal{D}_{\text{IDK}}}\left[\log \sigma\left(-\beta\log \frac{p(y' \mid x; \theta)}{p(y \mid x; \theta)}\right)\right],\]where \(\sigma(\cdot)\) is the sigmoid function, \(\beta\) is a hyper-parameter.
The gradient of AP loss w.r.t. the model parameters is:
\[\nabla_\theta\mathcal{L}_{\text{AP}}(\theta) = \mathbb{E}_{\mathcal{D}_R,\mathcal{D}_{\text{IDK}}}[W_\theta(x, y, y')\nabla_\theta (\log p(y' \mid x; \theta) - \log p(y \mid x; \theta))].\]The \(W_\theta(x, y, y') = 1/(1 + (\frac{p(y \mid x; \theta)}{p(y' \mid x; \theta)})^\beta)\) can be regarded as an adaptive gradient weight.
Given a question \(x\) in \(\mathcal{D}_R\), in the early stage of unlearning process, where \(p(y \mid x; \theta) \gg p(y' \mid x; \theta)\), we have \(W_\theta(x, y, y') \ll 1\).
As the unlearning proceeds, either a decrease in \(p(y \mid x; \theta)\) or an increase in \(p(y' \mid x; \theta)\) will result in a larger \(W_\theta(x, y, y')\), thereby providing stronger regularization. The gradient of AP loss consists of two terms in addition to the adaptive weight. The first term is equivalent to GA on the rejection template, which satisfies the first objective. The second term is equivalent to GD on the original answer, which satisfies the second objective.
My interpretation of the above equation is as follows:
- Reminder that in gradient descent, we follow the negative gradient direction to update the model parameters, i.e., \(\theta \leftarrow \theta - \eta \nabla_\theta \mathcal{L}\)
- In the first term, we follow the negative direction of \(\nabla_\theta (\log p(y' \mid x; \theta)\) - which aims to reduce the probability of \(P(\mathcal{Y}_{IDK} \mid \mathcal{X}_R)\)
- In the second term, we follow the direction of \(\nabla_\theta (\log p(y \mid x; \theta)\) - which aims to increase the probability of original answer \(P(y \mid \mathcal{X}_R)\)
Large Language Models Unlearning
Proposed method: Machine Unlearning for LLMs.
- Requires negative examples only, which are easier to collect. (through user reporting or red teaming)
- It is less computationally expensive, the cost is comparable to fine-tuning. RLHF is slow due to the need of generating samples from the fine-tuned model at current step.
- It is more effective when we know which training samples cause the misbehavior.
Simple method - Gradient Ascent
\[\theta_{t+1} = \theta_t + \lambda \nabla_{\theta} \mathcal{L}(\theta_t)\]where $\mathcal{L}(\theta_t)$ is the loss function of the model at step $t$ and $\lambda$ is the unlearning rate. This changes the model parameters to not reduce but increase the loss function at the negative examples.
Proposed method
\[\theta_{t+1} = \theta_t - \epsilon_1 \nabla_{\theta} \mathcal{L}_{\text{fgt}} - \epsilon_2 \nabla_{\theta} \mathcal{L}_{\text{rdn}} - \epsilon_3 \nabla_{\theta} \text{KL}_{\text{nor}}\]More specifically:
- \(\mathcal{L}_{\text{fgt}} = - \sum_{(x,y) \in D^{\text{fgt}}} \mathcal{L}(x,y;\theta)\): forgetting loss, aiming to make the model forget the negative examples. \(D^{\text{fgt}}\) is the set of negative examples and \(\mathcal{L}\) represents the LLM loss function \(\mathcal{L}(x,y;\theta) = \sum_{i=1}^{\| y \|} l(h_{\theta}(x, y_{<i}), y_i)\). In the experiements, the authors made use of the harmful Q&A pairs from PKU-SafeRLHF dataset.
- \(\mathcal{L}_{\text{nor}} = \sum_{(x,y) \in D^{\text{nor}}} \sum_{i=1}^{\| y \|} \text{KL} (h_{\theta^o} (x, y_{<i}) \parallel h_{\theta} (x, y_{<i}))\): preserving loss, to make sure the model still performs well on the normal examples. \(D^{\text{nor}}\) is the set of normal examples. In the experiments, the authors used the TruthfulQA dataset as the normal set.
- \(\mathcal{L}_{\text{rdn}} = - \sum_{(x,.) \in D^{\text{fgt}}, y \in Y^{\text{rdn}}} \mathcal{L}(x,y;\theta)\): random matching loss, to force the model to generate random outputs \(y \in Y^{\text{rdn}}\) on the target queries \(x(x,.) \in D^{\text{fgt}}\).
The third term is a bit tricky that requires a further explaination to me. The authors mentioned in Section 4 that the random matching loss empirically helps both the forgetting and preserving tasks. It is also interesting to see that in preserving loss, the authors used the KL divergence instead of the cross-entropy loss. As explained in Section 3, performance on normal prompts deteriorates easily after unlearning and preserving performance on normal samples is generally harder to achieve than forgetting harmfulness. The KL divergence is a good choice to measure the difference between the fine-tuned model’s output and the original model’s output than the cross-entropy loss which is less sensitive to the difference.
How to evaluate
-
Unlearn performance: In terms of evaluating outputs on harmful prompts, the authors used harmful rate flagged by the PKU moderation model. They also used fluency (the perplexity of generated text tested on OPT-2.7B) and diversity (the number of unique tokens in the generated text) to evaluate the unlearned model. A low perplexity and high diversity are desired.
-
Preserve performance: In terms of evaluating outputs on normal prompts, the authors used the BLEURT score to measure the similarity between the outputs on the normal prompts generated by the unlearned model and the original model. They also evaluated the utility rewards on responses on the TruthfulQA test dataset.
References
Enjoy Reading This Article?
Here are some more articles you might like to read next: