In 2023, when the work on Controllable Diffusion Models was just starting its momentum, with the several key milestones papers Textual Inversion, Dreambooth and ControlNet, I had predicted that there will be an interesting research direction on Anti-Personalization in the future.

Not long after Dreambooth was released, there are several papers on Anti-Personalization had been published, including Anti-Dreambooth and Adversarial Diffusion papers.

In August 2023, when finishing my PhD and starting my postdoc, I had the chance to switch my research from Adversarial Machine Learning (attack and defense on traditional classification models) to a more modern and exciting field Trustworthy Generative AI. However, at that time, I piloted with Anti-Textual Inversion, because I believe in the potential of Textual Inversion over Dreambooth, but unfortunately, the personalization performance of TI was not as good as Dreambooth, making the problem of Anti-Personalization with the base model TI was not as interesting anymore.

Moreover, I have enough experience with Adversarial Machine Learning to understand that adding invisible noise to an image as a defense mechanism is not robust and easy to be bypassed by simple techniques such as image transformations, denoising autoencoders, etc. It likes if you are the defender, you are always one step behind the attacker.

I switched to Machine Unlearning for Generative Models and fortunately, got some successful on this direction with three papers: NeurIPS 2024, ICLR 2025 and ICLRW 2025.

Now, after 2 years, because of the needed of the project that I am working on (with Department of Defence Australia), I have to switch back to Anti-Personalization.

That is the context of this post. I will review the key papers on Anti-Personalization in the last 2 years, and also some thoughts on the future of this direction.

Background

Textual Inversion

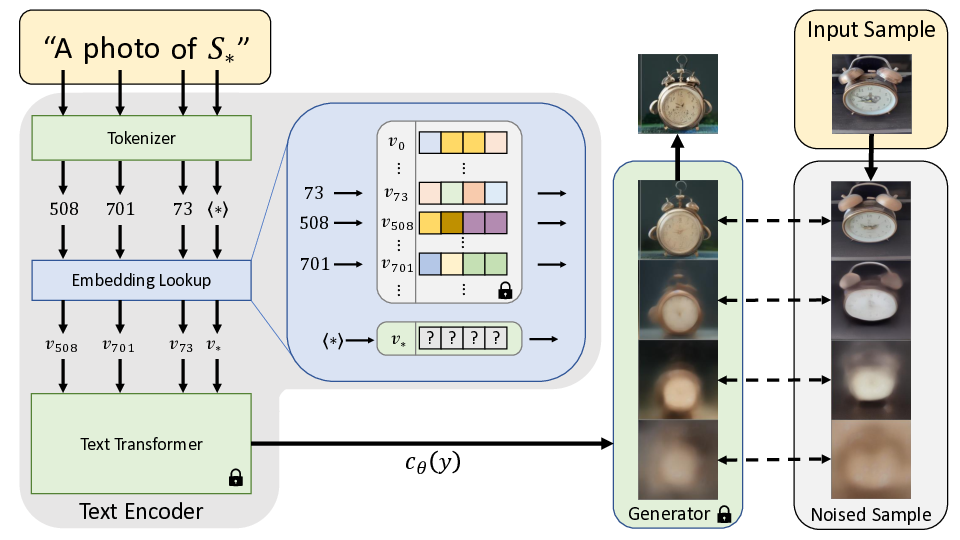
Textual Inversion [1]. A string S* containing our placeholder word is first converted into tokens. These tokens are converted to continuous vector representations (the "embeddings", v). Finally, the embedding vectors are transformed into a single conditioning code c_θ(y) which guides the generative model. We optimize the embedding vector v* associated with our pseudo-word S*, using a reconstruction objective.

The optimization objective is:

\[v_* = \text{argmin}_v \mathbb{E}_{z\sim\mathcal{E}(x), y, \epsilon \sim \mathcal{N}(0, 1), t }\Big[ \Vert \epsilon - \epsilon_\theta(z_{t},t, c_\theta(y)) \Vert_{2}^{2}\Big]\]

where v* is the embedding vector associated with the placeholder word S*.

Dreambooth

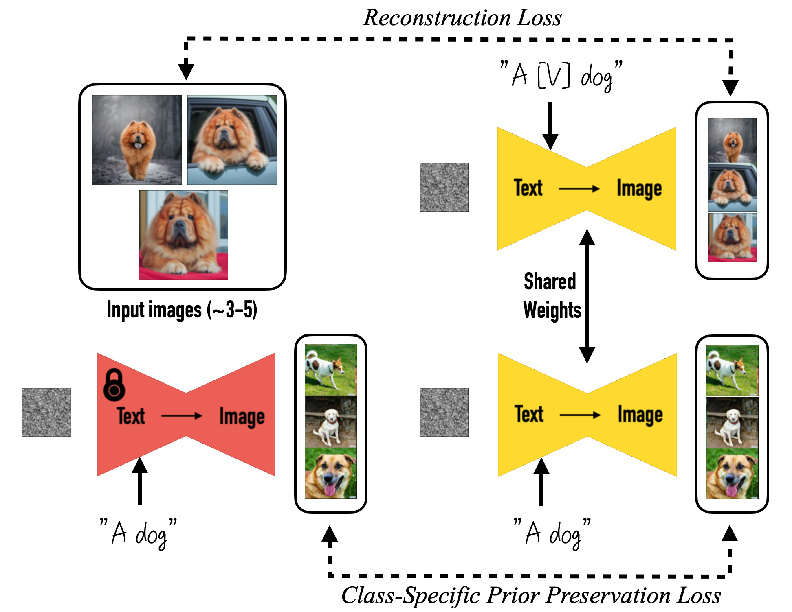
Dreambooth's Fine-tuning [1]. Given ~3-5 images of a subject we fine-tune a text-to-image diffusion model with the input images paired with a text prompt containing a unique identifier and the name of the class the subject belongs to (e.g., "A [V] dog"), in parallel, we apply a class-specific prior preservation loss, which leverages the semantic prior that the model has on the class and encourages it to generate diverse instances belong to the subject's class using the class name in a text prompt (e.g., "A dog").

The optimization objective of Dreambooth is:

\[\mathbb{E}_{\mathbf{x}, \mathbf{c}, \mathbf{\epsilon}, \mathbf{\epsilon}^{'},t} \left[ w_t \| \hat{\mathbf{x}}_\theta (\alpha_t \mathbf{x} + \sigma_t \mathbf{\epsilon}, \mathbf{c}) - \mathbf{x}\|_2^2 + \lambda w_{t^{'}} \| \hat{\mathbf{x}}_\theta(\alpha_{t^{'}} \mathbf{x}_\text{pr} + \sigma_{t^{'}} \mathbf{\epsilon}^{'}, \mathbf{c}_\text{pr}) - \mathbf{x}_\text{pr} \|_2^2 \right]\]

where \(c_\text{pr}\) is the conditioning vector of the prior class (e.g., “A dog”), \(c\) is the conditioning vector of the specific/keyword class (e.g., “A [V] dog”), \(\mathbf{x}_\text{pr}\) is the image of the prior class (e.g., a normal dog from Internet) \(\mathbf{x}\) is the image of the specific/keyword class (e.g., a target dog in the user’s dataset).

\(\alpha_t, \sigma_t, w_t\) are terms that control the noise schedule, sample quality, and are funetions of the diffusion process at time step \(t\).

PhotoGuard - Raising the Cost of Malicious AI-Powered Image Editing (ICML 2023)

At the same time with the AdvDM (or MIST) paper, this paper also proposed a

Adversarial Example Does Good: Preventing Painting Imitation from Diffusion Models via Adversarial Examples (ICML 2023)

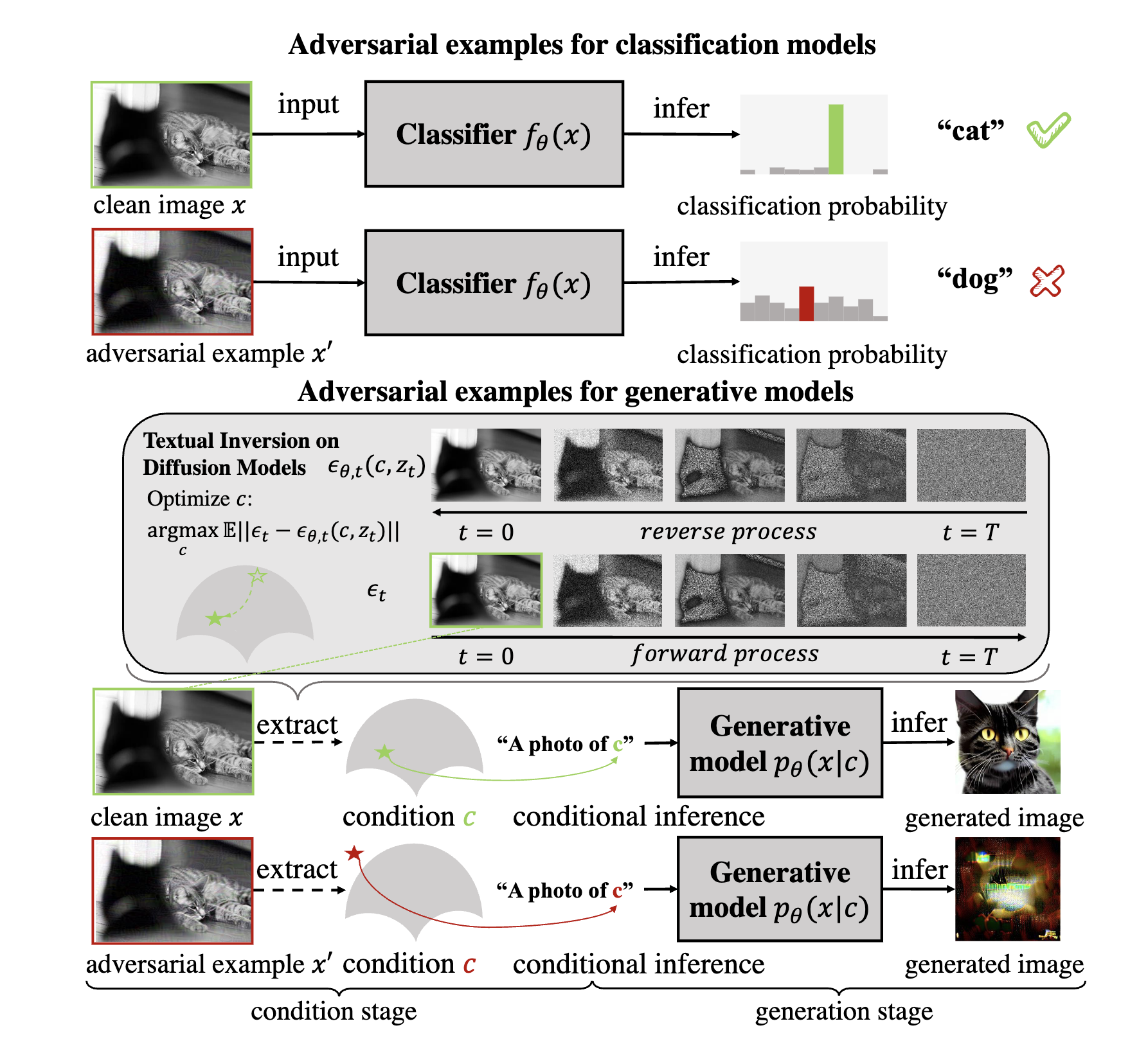
Comparison of workflows for adversarial examples in classification models and diffusion models. Adversarial examples in diffusion models prevent diffusion models from extracting image features as conditions by inducing out-of-distribution features. The feature extracting shown in the figure is textual inversion. Image from Liang et al. 2023

High level idea: Adversarial examples for Textual Inversion. It is just that simple. One month later, Anti-Dreambooth was published on Arxiv. The two low hanging fruits were picked.

In the paper, the authors described the optimization objective as follows:

\[\delta = \text{argmax}_{\delta} \mathbb{E}_{x^{'}_{1:T} \sim u(x^{'}_{1:T})} - \log \frac{p_{\theta}(x^{'}_{0:T})}{q(x^{'}_{1:T} \mid x^{'}_0)}\]

where \(x^{'} = x + \delta\) is the adversarial example, \(u(x^{'}_{1:T})\) is the uniform distribution of the adversarial example over the time steps, \(q(x^{'}_{1:T} \mid x^{'}_0)\) is the posterior distribution that can be computed by the forward diffusion process, and \(p_{\theta}(x^{'}_{0:T})\) is the parameterized distribution aiming to approximate the posterior distribution \(q(x^{'}_{1:T} \mid x^{'}_0)\).

While looking scary (as intended by the authors), the nice thing of Diffusion Models is that the above optimization objective can be simplified to the form of matching the predicted noise with the true noise. See my tutorial on Diffusion Models for more details.

\[\delta = \text{argmax}_{\delta} \mathbb{E}_{x^{'}_{1:T} \sim u(x^{'}_{1:T})} \left[ \| \epsilon_\theta (x^{'}_{t}, t) - \epsilon_t \|^2 \right]\]

where \(x_t = \sqrt{\bar{\alpha}_t} (x_0 + \delta) + \sqrt{1-\bar{\alpha}_t} \epsilon\) as in the forward diffusion process.

Anti-Dreambooth (ICCV 2023)

Anti-Dreambooth [1]

Idea: Reverse/Attack the learning process of the Dreambooth by learning the adversarial perturbation \(\delta^{(i)}\) associated with each image \(x^{(i)}\) in the training dataset.

The optimization objective is:

\[\begin{align*} \delta^{*(i)} &= \text{argmax}_{\delta^{(i)}} \mathcal{L}_{cond}(\theta^*, x^{(i)} + \delta^{(i)}), \forall i \in \{1,..,N_{db}\}, \\ \text{s.t.} \quad & \theta^* = \text{argmin}_{\theta} \sum_{i=1}^{N_{db}} \mathcal{L}_{db}(\theta, x^{(i)} + \delta^{(i)}), \\ \text{and} \quad & \Vert \delta^{(i)} \Vert_p \leq \eta \quad \forall i \in \{1,..,N_{db}\}, \end{align*}\]

where \(\mathcal{L}_{db}\) is the DreamBooth’s loss function and \(\mathcal{L}_{cond}\) is the conditional loss function, e.g., reconstruction loss so that the model \(\theta^*\) cannot generate the image \(x^{(i)}\).

\[\mathbb{E}_{\mathbf{x}, \mathbf{c}, \mathbf{\epsilon}, \mathbf{\epsilon}^{'},t} \left[ \underbrace{w_t \| \hat{\mathbf{x}}_\theta (\alpha_t \mathbf{x} + \sigma_t \mathbf{\epsilon}, \mathbf{c}) - \mathbf{x}\|_2^2}_{\mathcal{L}_{recon}} + \lambda \underbrace{ w_{t^{'}} \| \hat{\mathbf{x}}_\theta(\alpha_{t^{'}} \mathbf{x}_\text{pr} + \sigma_{t^{'}} \mathbf{\epsilon}^{'}, \mathbf{c}_\text{pr}) - \mathbf{x}_\text{pr} \|_2^2}_{\mathcal{L}_{prior}} \right]\]

FastProtect - Nearly Zero-Cost Protection Against Mimicry by Personalized Diffusion Models (CVPR 2025)

FastProtect [1]

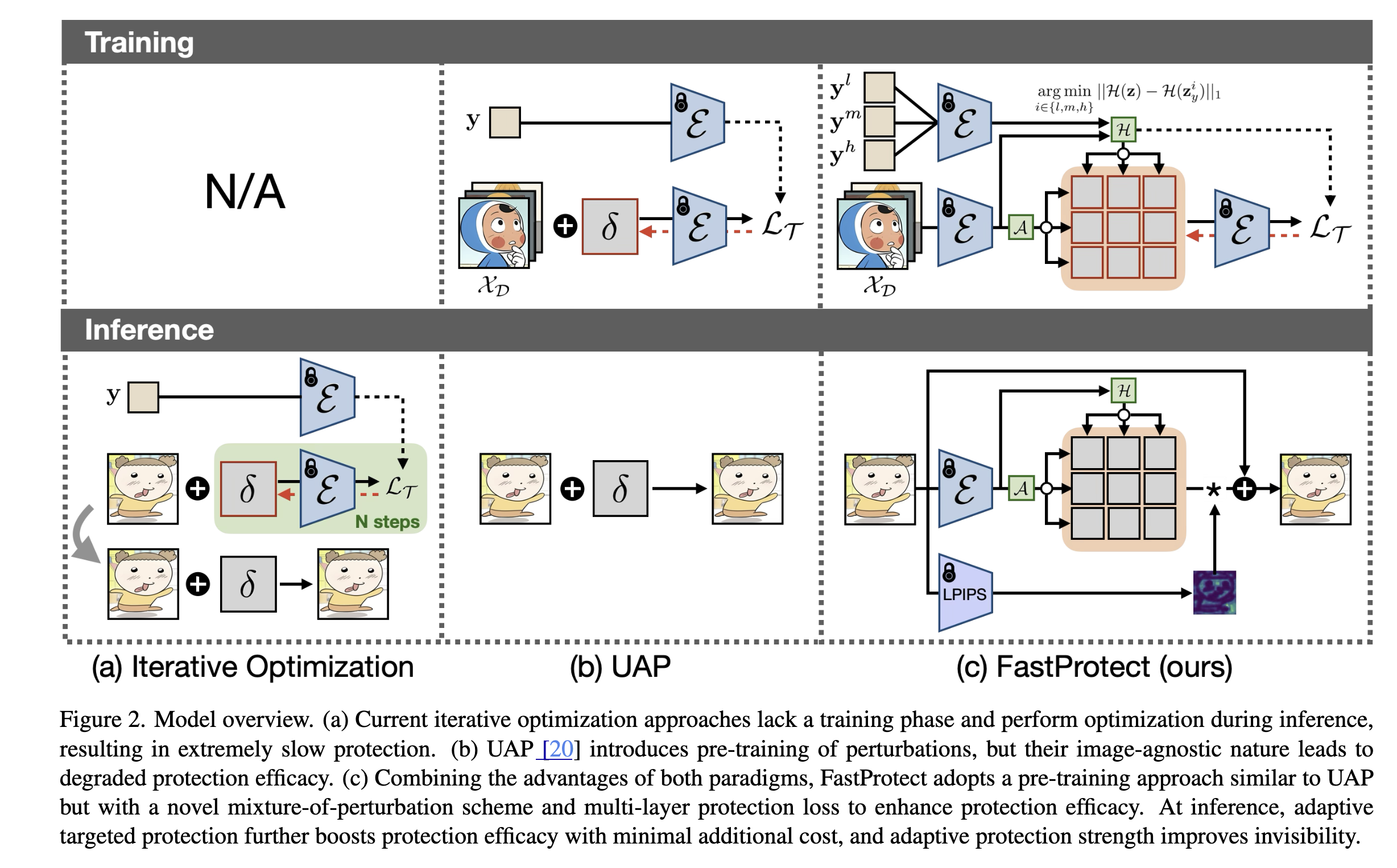
Mixture-of-Perturbation (MoP)

\[\hat{x} = x + \delta_g + \Delta_k, \quad \text{where} \quad k = \mathcal{A}(\Epsilon(x))\]

where \(\delta_g\) is a global perturbation which is found by gradient ascent approach as in AdvDM or PhotoGuard. The new contribution of this paper is the \(\Delta_k\) term, which comes from Mixture-of-Perturbation (MoP) \(\Delta = {\delta_1, \delta_2, \dots, \delta_K}\) where \(\delta_k\) is a perturbation found by gradient descent approach.