MS-Diffusion - Multi-subject Zero-shot Image Personalization with Layout Guidance (ICLR 2025)
Link to the paper: MS-Diffusion: Multi-subject Zero-shot Image Personalization with Layout Guidance
Link to github: MS-Diffusion

Key contributions
Challenges

Personalizing with multiple subjects is challenging, specifically:
- Subject neglect: one or more subjects are not properly represented in the generated image.
- Subject overcontrol: The output does not match with the input prompt (e.g., “a dog and a cat on the beach” - but the output is not on the beach). The appearance or placement of a subject is unduly influenced by its reference image, potentially overriding the textual prompt or other subject conditions.
- Subject-subject conflict: where the interaction between multiple subjects in the generated image is unrealistic or undesirable, i.e., two similar dog and cat.
The reasons for these challenges are:
- Difficulty in feature representation: compare to text embedding, image embedding are generally sparser and contain more information, making their projection into the condition space more difficult. The pooled output from the image encoder can omit many details (discussed in Section 3.4 of the paper). This can lead to a loss of granular details of individual subjects.
- Complexity of Multi-subject interaction and control: Ensuring that the generated image aligns with the textual prompt while maintaining the correct placement and appearance of each subject is challenging.
Contributions
- Grounding Resampler: A modified cross-attention layer that uses concatenated image and text embeddings as the condition embedding.
- Data Construction: A data construction pipeline to collect a large amount of data with multiple subjects in the same image.
- Multi-subject Cross-attention with Masks: A modified cross-attention layer that uses subject-specific masks to guide the model to pay attention to the subject.
Background: Stable Diffusion with Image Prompt
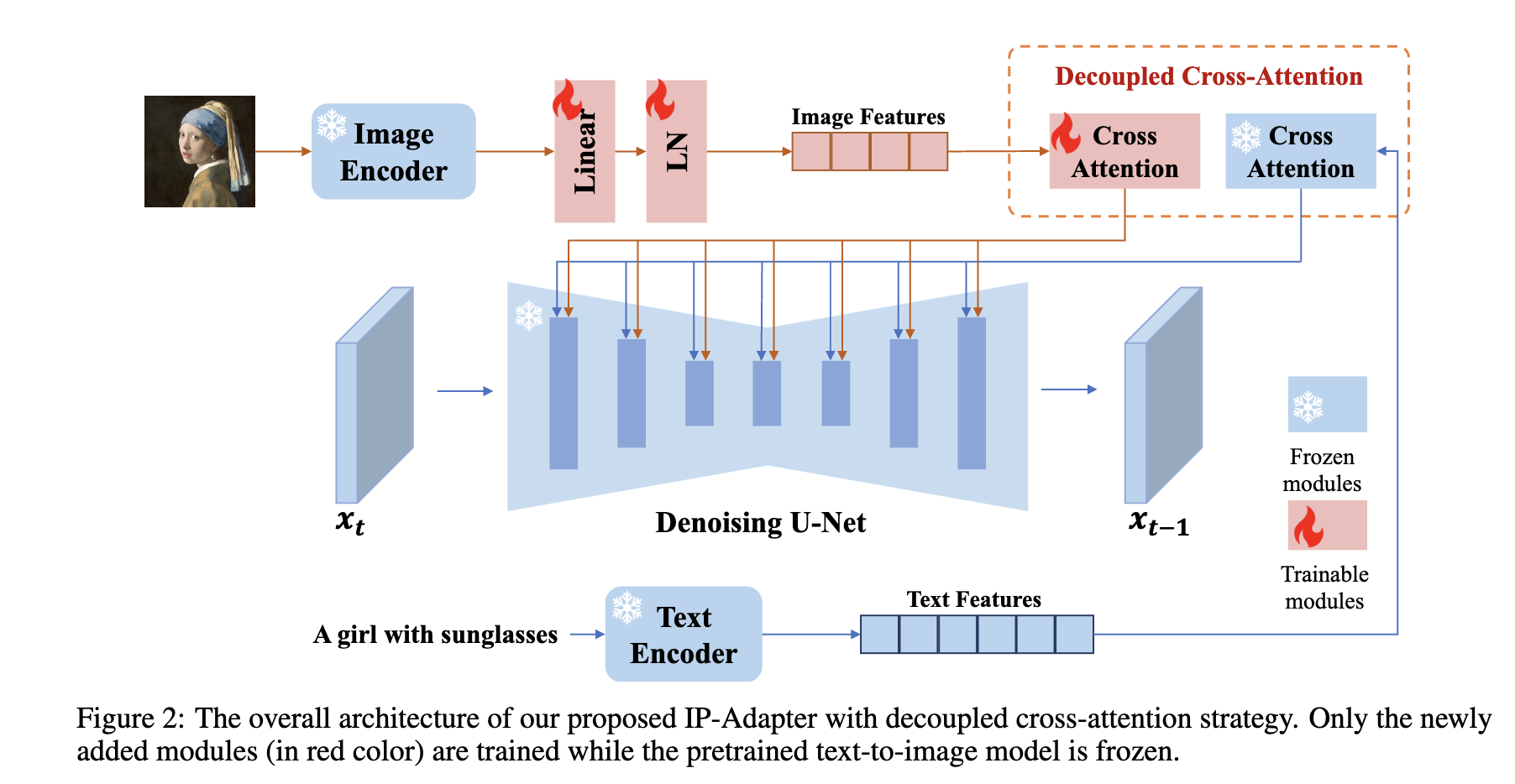
Beyond controlling the generation process using text prompt, there is a hot topic in the community to control using image information/layout/prompt - which has a huge potential in applications, e.g., image inpainting, image-to-image generation, etc. In the standard Stable Diffusion, the condition embedding \(c_t\) is just a text embedding \(c_t = E_t(y)\) where \(y\) is the text prompt and \(E_t\) is a pre-trained text encoder such as CLIP. IP-Adapter [1] proposes to use an additional image encoder to extract the image embedding from a reference image \(c_i = E_i(x)\) and then project it into the original condition space. The objective function for IP-Adapter is:
\[\mathcal{L}_{IP} = \mathbb{E}_{z, c, \epsilon, t} \left[ \mid \mid \epsilon - \epsilon_\theta(z_t \mid c_i, c_t, t) \mid \mid_2^2 \right]\]The cross-attention layer is also modified from the one in Stable Diffusion to include the image embedding \(c_i\) as a condition.
\[\text{Attention}(Q, K_i, K_t, V_i, V_t) = \lambda \text{softmax}\left(\frac{QK_i^T}{\sqrt{d}} + c_i\right)V_i + \text{softmax}\left(\frac{QK_t^T}{\sqrt{d}}\right)V_t\]where \(Q=z W_Q\), \(K_i = c_i W_K^i\), \(K_t = c_t W_K^t\), \(V_i = c_i W_V^i\), \(V_t = c_t W_V^t\), and \(W_Q\), \(W_K^i\), \(W_K^t\), \(W_V^i\), \(W_V^t\) are the weights of the linear layers. The model becomes the original Stable Diffusion when \(\lambda = 0\).
Proposed Method
Grounding Resampler
\[\text{RSAttn} = \text{softmax}\left( \frac{Q(f_q) K^T([c_i, c_q])}{\sqrt{d}} \right) V([c_i, c_q])\]where \(c_q\) is the learnable query feature, \(c_i\) is the image embedding.
My interpretation:
- The grounding resampler is a modified cross-attention layer that uses the image embedding and the learnable query feature to generate the attention score.
- Compared to the previous IP-Adapter which uses the image and text embeddings separately, the \(\text{RSAttn}\) uses the concatenation of the two embeddings as the unified condition embedding.
Data Construction
The authors propose a data construction pipeline to collect a large amount of data with multiple subjects in the same image. \(c_q\) was initialized by the text embedding of the entities (e.g., “dog”, “cat”, “beach”) and then optimized during training. \(c_i\) is the image embedding of corresponding subject - detected by an additional object detector.
To prevent the model becoming overfitted/dependent on the grounding tokens (e.g., “dog”, “cat”) during inference (?), the authors proposed to randomly replace these tokens with the original learnable queries in the training (?).
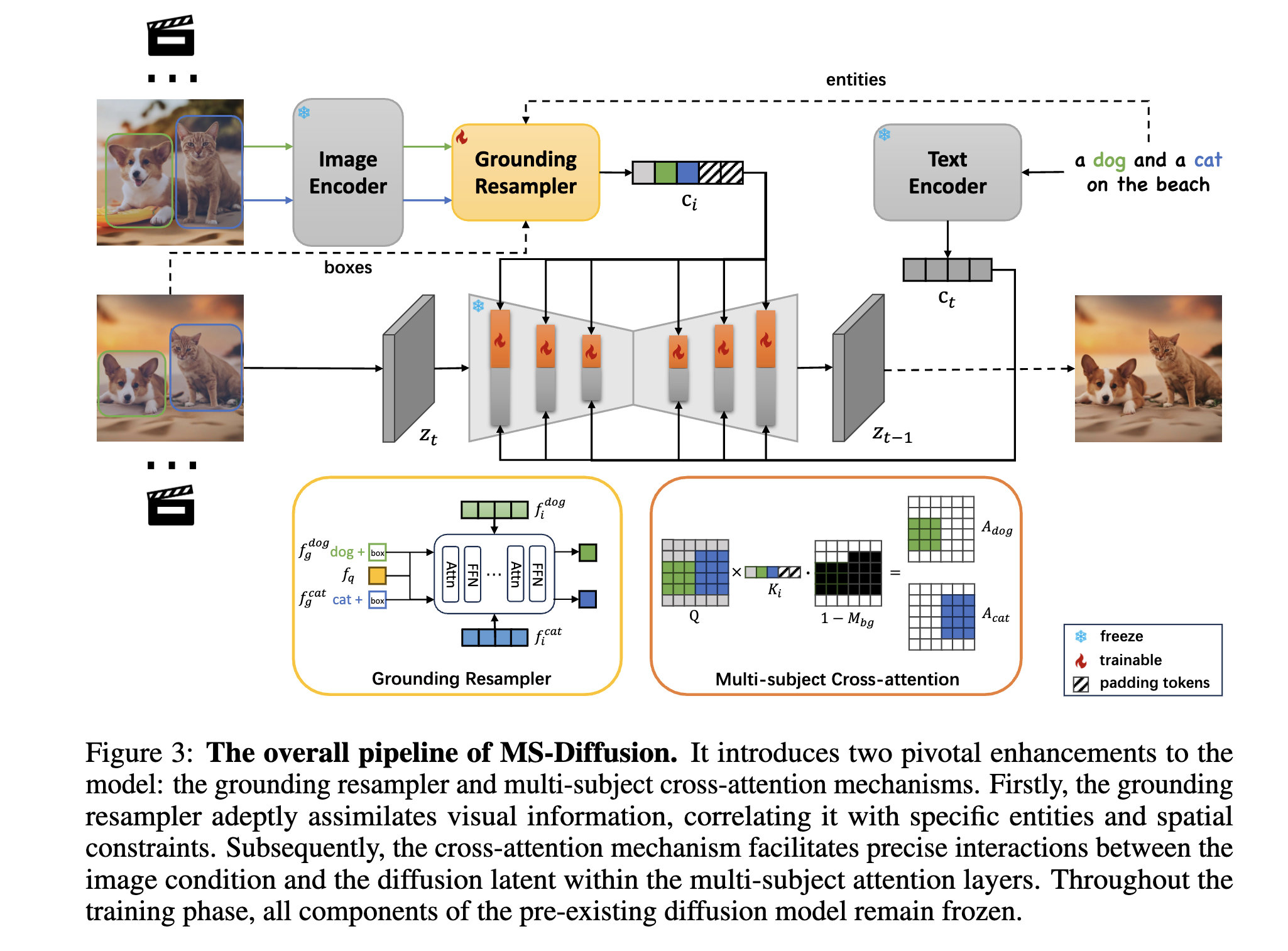
Multi-subject Cross-attention
The idea is to incorporate attention masks within cross-attention layers to focus on the relevant subjects and exclude other irrelevant in the text prompt and visual prompt.
\[\mathbf{M}_j(x, y) = \begin{cases} 0 & \text{if } [x, y] \in B_j \\ -\infty & \text{if } [x, y] \notin B_j \end{cases}\]Here, \(B_j\) denotes the coordinate set of bounding boxes related to the \(j\)th subject. By this means, the conditional image latent \(\hat{\mathbf{z}}_{img}\) is derived through:
\[\hat{\mathbf{z}}_{img} = \text{Softmax}\left(\frac{\mathbf{Q}\mathbf{K}_i^\top}{\sqrt{d}} + \mathbf{M}\right)\mathbf{V}_i\]Herein, \(\mathbf{M}\) represents the concatenation of all subject-specific masks, \(\text{Concat}(\mathbf{M}_0,\ldots,\mathbf{M}_n)\). In this way, the model ensures each subject to be represented in a certain area, thus resolving the issues of subject neglect and conflict.
Mask for Background
\[\mathbf{M}_{bg}(x, y) = \begin{cases} 1 & \text{if } [x, y] \in B_{bg} \\ 0 & \text{if } [x, y] \notin B_{bg} \text{ a.k.a. subjects} \end{cases}\]The mask for background is a matrix of the same size as the image, with the value of \(1\) for the background and \(0\) for the subjects.
\[\mathbf{z}_{img} = (1 - \mathbf{M}_{bg}) \odot \mathbf{z}_{img}\]Where \(\odot\) is the element-wise multiplication. This operation ensures that the background is removed from the image latent. As the authors mentioned, this approach is to ensure that text conditions predominate over areas lacking of any guided information (a.k.a. background).
My interpretation:
- The mask \(\mathbf{M}\) is a matrix of the same size as the image, with the value of \(-\infty\) for the background and \(0\) for the subject.
- The mask is added to the attention score matrix \(\mathbf{Q}\mathbf{K}_i^\top\) to guide the model to pay attention to the subject.
Question: Where the \(\mathbf{z}_{img}\) is used? The authors did not use a consistent notations throughout the paper.
Enjoy Reading This Article?
Here are some more articles you might like to read next: